|
|
Revista de Educación Estadística Vol. 4, pp. 1-25, ene. 2025 - dic. 2025 ISSN 2810-6164 |
DOI: https://doi.org/10.29035/redes.4.1.2
CARACTERIZACIÓN DEL CONOCIMIENTO MATEMÁTICO PARA LA ENSEÑANZA DE ESPACIOS MUESTRALES EN DOCENTES DE EDUCACIÓN PRIMARIA COSTARRICENSE
Caracterização do conhecimento matemático para o ensino de espaços amostrais em professores do ensino fundamental da Costa Rica
Characterization of mathematical knowledge for the teaching of sample spaces in costa Rican Primary Education teachers
Luis A. Hernández-Solís1
Universidad Estatal a Distancia (San José, Costa Rica)
Cristian Quesada-Fernández2
Universidad Estatal a Distancia (San José, Costa Rica)
Eric Padilla-Mora3
Universidad Estatal a Distancia (Costa Rica)
Resumen
El objetivo del trabajo fue analizar el conocimiento matemático para la enseñanza de espacios muestrales en docentes en ejercicio de la educación primaria costarricense. Para ello se evaluaron los subdominios CCK, HCK y el SCK del modelo Mathematical Knowledge for Teaching (MKT) referentes a dicho contenido mediante un cuestionario con tres ítems que requerían de la enumeración, comprensión y construcción de espacios muestrales. Se analizaron las respuestas al cuestionario de 124 educadores de las seis regiones socioeconómicas en que se divide Costa Rica. Los resultados señalan debilidades en la enumeración asociados a poco conocimiento de técnicas de conteo; así como la confusión de los eventos seguro e imposible, con evento muy probable y poco probable, respectivamente. En el análisis de didáctico de respuestas ficticias de estudiantes casi las tres cuartas partes de los docentes indicó como incorrecta la única respuesta correcta, señalando respuestas incorrectas como correctas, evidenciando en algunos casos la presencia del sesgo de equiprobabilidad.
Palabras clave: probabilidad, educación primaria, didáctica de la probabilidad, espacio muestral, formación de profesores.
Resumo
O objetivo deste estudo foi analisar o conhecimento matemático para o ensino de espaços amostrais entre professores atuantes do ensino fundamental na Costa Rica. Para tanto, foram avaliados os subdomínios CCK, HCK e SCK do modelo Conhecimento Matemático para o Ensino (MKT) relativos ao referido conteúdo, por meio de um questionário com três itens que exigiam enumeração, compreensão e construção de espaços amostrais. Foram analisadas as respostas do questionário de 124 educadores das seis regiões socioeconômicas em que a Costa Rica está dividida. Os resultados indicam fragilidades na enumeração associadas ao pouco conhecimento de técnicas de contagem; bem como a confusão de eventos certos e impossíveis com eventos muito prováveis e improváveis, respectivamente. Na análise didática das respostas fictícias dos alunos, quase três quartos dos professores indicaram a única resposta correta como incorreta, marcando as respostas incorretas como corretas, evidenciando em alguns casos a presença de viés de equiprobabilidade.
Palavras-chave: probabilidade, ensino fundamental, didática da probabilidade, espaço amostral, formação de professores.
Abstract
The objective of the work was to analyze the mathematical knowledge for teaching sample spaces in active Costa Rican primary education teachers. It was evaluated in this work the CCK, HCK and SCK subdomains of the Mathematical Knowledge for Teaching (MKT) model, related to this content, were evaluated, through a questionnaire with three items that required the enumeration, understanding and construction of sample spaces. The responses to the questionnaire from 124 educator from the six socioeconomic regions into which Costa Rica is divided were analyzed. The results point out weaknesses in the enumeration of different sample spaces, associated with little knowledge of counting techniques; as well as the confusion of certain and impossible events, with very probable and unlikely events, respectively. In the didactic analysis of students’ fictitious answers, almost three-quarters of the teachers indicated the only correct answer as incorrect, indicating incorrect answers as correct, evidencing in some cases the presence of equiprobability bias.
Keywords: probability, primary education, probability teaching, sample space, teacher training.
Recibido: 13/10/2024 - Aceptado: 23/12/2024
1. INTRODUCCIÓN
La convivencia con el azar y la incertidumbre en diversos ámbitos de la vida cotidiana, fundamentan la importancia de desarrollar el razonamiento probabilístico en el ciudadano actual (Batanero et al., 2023). El estudio de la probabilidad expone las limitaciones de argumentos puramente deductivos, teniendo esto un alto valor educativo (Pino y Estrella, 2012), además su relevancia en distintas áreas profesionales y científicas ha hecho que los conocimientos probabilísticos formen parte los objetivos de alfabetización matemática en las últimas décadas (Jones et al., 2007; Nilsson y Li, 2015), incluso aconsejándose iniciar desde la educación infantil (Alsina, 2017; Batanero et al., 2021; Vásquez y Alsina, 2019). Esto ha incido en que cada vez más los contenidos de probabilidad tengan mayor notoriedad en los currículos de matemáticas a nivel mundial, así como en las evaluaciones internacionales de la Organización para la Cooperación y Desarrollo Económico (OECD), específicamente, mediante el Programa para la Evaluación Internacional de los Estudiantes (PISA, por sus siglas en Inglés), en el cual aparece, como uno de sus dominios o categorías, “incertidumbre y datos”, evaluando la competencia matemática a partir de ítems con contextos altamente variables o donde existe la incertidumbre, en los cuales se busca que los estudiantes tomen decisiones y hagan predicciones a partir de la interpretación de la información estadística mostrada (OCDE, 2023).
En el ámbito costarricense, desde 1995 aparecen contenidos de probabilidad en el currículo de Matemáticas, pero solo para la Educación Primaria; por lo que no se le daba continuidad en Educación Secundaria; además, de que se incluían pocos temas, comparado con los de aritmética y geometría. Es hasta los Programas de Estudio de Matemáticas para la educación preuniversitaria, aprobados en el 2012 (MEP, 2012), que se le da mayor protagonismo al área de Estadística y Probabilidad, afirmando que “El lugar relevante que se da a esta área obedece al papel que juega la información y el manejo del azar en la sociedad moderna” (MEP, p. 55). Sin embargo, esto ha significado un gran desafío, particularmente, para los docentes de educación primaria, tanto en conocimiento matemático como en su didáctica. Otro aspecto por destacar es que esa poca presencia de la Probabilidad en los planes de estudio anteriores hizo que los programas de formación inicial de docentes, no le dieran la importancia requerida al desarrollo de conocimientos y habilidades referentes a la Probabilidad y su enseñanza; lo que provocó que los docentes de Educación Primaria costarricense manifiesten inconformidad con la formación recibida en estos temas (Alpízar et al., 2012; Alpízar et al., 2015).
Conscientes de esta realidad y con la finalidad de contribuir y apoyar a los docentes de I y II Ciclo de la educación costarricense en el proceso de enseñanza de la Probabilidad, desde la carrera Enseñanza de la Matemática de la Universidad Estatal a Distancia de Costa Rica, se desarrolla el proyecto Fortalecimiento del conocimiento profesional de la persona docente de Educación Primaria en probabilidad y su didáctica, en el cual como parte de las acciones, se realizó un diagnóstico con el fin de determinar y analizar los conocimientos de contenido y pedagógicos que poseen 124 docentes en ejercicio de diversas Direcciones Regionales Educativas del país, y así diseñar un plan de capacitación. Este artículo tiene como objetivo mostrar algunos de los resultados obtenidos a partir de la evaluación aplicada, enfocados principalmente en el tema de espacios muestrales.
2. FUNDAMENTOS
El trabajo se fundamenta en el modelo del conocimiento matemático para la enseñanza (Mathematical Knowledge for Teaching, MKT) de Ball et al. (2008) y los antecedentes sobre comprensión del espacio muestral, de lenguaje probabilístico y de estudios del Conocimiento Profesional del Profesor, que se resumen a continuación.
2.1. Modelo Conocimiento Matemático para la Enseñanza (MKT)
Los primeros estudios referentes al conocimiento profesional del profesor surgieron con el objetivo de identificar la especificidad de un conjunto de conocimientos propios de la enseñanza que le permita al educador ser visto como un profesional (Escudero et al., 2015). Algunas investigaciones (Grossman, 1990; Shulman, 1986, 1987) han desarrollado diferentes propuestas acerca de los componentes del conocimiento base para la enseñanza que un profesor debería tener para su labor docente. Shulman (1986), en particular, origina un cambio de paradigma, ya que no solo se preocupa por lo que “debe saber” el profesor, sino también por lo que “debe saber hacer”. Otros autores (e. g. Ball et al., 2008; Carrillo et al., 2013; Godino et al, 2017) se han enfocado específicamente en el conocimiento profesional del profesor de Matemática.
El modelo conocimiento matemático para la enseñanza (MKT) (Ball et al., 2008), se divide en dos dominios, conocimiento del contenido y conocimiento pedagógico del contenido que, a su vez, se dividen es tres subdominios cada uno. De los seis subdominios y de acuerdo con lo que se analiza en este artículo serán considerados tres de ellos, los cuales se describen a continuación:
• Conocimiento Común del Contenido - Common Content Knowledge (CCK). Es el conocimiento del tema que tiene el estudiantado o cualquier persona educada; es decir, permite a la persona docente resolver las tareas que propone a sus estudiantes; pero no es un conocimiento especial del profesor (Hill et al., 2008).
• Conocimiento en el horizonte matemático - Horizon Content Knowledge (HCK). Se refiere a saberes matemáticos más avanzados que aportan diferentes perspectivas al profesorado; es decir, un conocimiento más amplio de la matemática en el cual un tema particular está situado. Tiene en cuenta aquellos componentes de la temática no incluidos en el currículo (en este caso de Educación Primaria), pero que son útiles para la enseñanza y proporcionan una comprensión más profunda.
• Conocimiento del contenido y los estudiantes - Knowledge of Content and Students (KCS). Se refiere al conocimiento que combina los saberes acerca del estudiantado y acerca de las matemáticas; es decir, cómo aprende un estudiante un contenido matemático, por ejemplo, incluye el conocer los errores que las personas estudiantes comenten con mayor frecuencia (Ball et al., 2008).
2.2. Currículo de Matemática costarricense
El Currículo de Matemáticas para la Educación Primaria (MEP, 2012), organizan el área de Estadística y Probabilidad de manera integrada, proponiendo el desarrollo de contenidos probabilísticos de manera gradual en cuanto a complejidad y precisión matemática. En la Tabla 1, se aprecia como algunas nociones básicas se desarrollan desde el primer curso hasta el último (6º curso) de este nivel educativo.
Tabla 1
Conocimientos probabilísticos que se desarrollan en la Educación Primaria del currículo de Matemática costarricense
|
Temas clave |
Curso |
|||||
|
1º |
2º |
3º |
4º |
5º |
6º |
|
|
Situaciones: aleatorias y seguras. |
x |
x |
x |
x |
||
|
Eventos: seguro, probable, imposible, más y menos probables. |
x |
x |
x |
x |
||
|
Resultados simples de un experimento aleatorio. |
x |
x |
x |
|||
|
Representación de eventos. |
x |
|||||
|
Definición clásica o laplaciana de probabilidad. |
x |
|||||
|
Propiedades de las probabilidades |
x |
|||||
Nota. Elaboración propia, con base en los Programas de Estudio de Matemáticas (MEP, 2012).
Es necesario señalar que, aunque el concepto de espacio muestral no se establece de forma directa y formal en la Educación Primaria, este se introduce como la totalidad de los resultados simples de un experimento aleatorio, lo cual es fundamental para resolver cualquier problema probabilístico (Lima et al, 2021; Nunes et al., 2014).
3. ANTECEDENTES
La relevancia que se le ha dado a la Probabilidad en los currículos escolares ha ocasionado que cada vez más los investigadores en educación matemática se interesen por estudiar el conocimiento del profesorado para enseñar estos temas. Al respecto Franco y Alsina (2022) realizaron una revisión de la bibliografía, entre el período 1997-2021, acerca de estudios asociados al conocimiento del profesorado de Educación Primaria para enseñar estadística y probabilidad; obteniendo que, de los 34 artículos identificados, 22 realizan el análisis con futuros docentes (64,7 %) y 12 con profesorado en ejercicio (35,3 %), lo cual indica un predominio en el conocimiento del futuro profesorado. Respecto al conocimiento para enseñar probabilidad, encontraron 21 estudios en total (61,7 %), de los cuales sólo siete se focalizan en el profesorado en activo.
En relación con el modelo de conocimiento profesional del profesor de Matemática., estos autores señalan que en los artículos analizados predomina el modelo MKT (35,0%). En cuanto a los estudios sobre el conocimiento para enseñar probabilidad, encuentran puntuaciones bajas en los diversos subdominios y/o facetas de conocimiento analizadas, lo cual refleja una escasa preparación del profesorado de Educación Primaria para la enseñanza de estos contenidos matemáticos.
Alonso-Castaño et al. (2021) propusieron a futuros profesores de educación primaria, crear y resolver un problema de probabilidad utilizando los valores de monedas de euro, diseñado para estudiantes de 11 a 12 años. Aunque encontraron evidencias de un adecuado conocimiento matemático común y especializado, en aproximadamente la mitad de la muestra, demasiados de ellos siguen mostrando una falta de conocimiento en ambos subdominios.
Vásquez y Alsina (2021) analizaron tareas de probabilidad propuestas a ocho profesores de educación primaria chilenos, centrándose en cinco componentes: recursos de enseñanza y aprendizaje; contextos probabilísticos; desafío cognitivo; procedimientos y estrategias; y significados de la probabilidad. Encuentran que las tareas de probabilidad se centran en la aplicación de fórmulas, de forma mecánica y sin significado, provocando que la clase de probabilidad se convierta en una clase aritmética. Como uno de los resultados relevantes, observan un nulo uso de recursos tecnológicos, un escaso uso de materiales físicos y un predominio absoluto de la resolución de ejercicios descontextualizados.
Kurt y Coşkuntuncel (2020) realizaron una evaluación del conocimiento del contenido de probabilidad a 98 futuros profesores de matemáticas, mediante un test de conocimiento del contenido de probabilidad tomado de Gómez-Torres (2014), traducido al turco, donde los participantes tuvieron más éxito en el conocimiento común del contenido, teniendo un nivel de comprensión suficiente para el significado clásico de probabilidad. Sin embargo, se observó que los candidatos a profesores presentaban deficiencias en el conocimiento ampliado del contenido (HCK) y en el conocimiento especializado del contenido (SCK), y que su comprensión del enfoque frecuentista y subjetivo de la probabilidad era insuficiente.
Rodríguez-Alveal et al. (2018) compararon el conocimiento sobre aspectos de alfabetización probabilística presentes en 30 profesores en activo y 15 en formación, encontrando que los primeros consiguen porcentajes de logro levemente superiores a los profesores en formación, ante situaciones problemáticas donde deben decidir de manera intuitiva si una sucesión es o no aleatoria.
Vásquez y Alsina (2017) analizaron las prácticas matemáticas de 93 profesores chilenos de educación primaria en activo a partir de un cuestionario que evaluaba el conocimiento común del contenido, mostrando un nivel de conocimientos insuficiente para la enseñanza de la probabilidad; específicamente, concluyeron que donde era necesario aplicar una adecuada comprensión de nociones básicas de probabilidad, tales como el espacio muestral, son de gran dificultad para los profesores.
Gómez-Torres (2014) evalúa el conocimiento común del contenido de 157 profesores en formación mediante un cuestionario con distintos ítems. También evaluó el conocimiento especializado del contenido y el conocimiento del contenido y los estudiantes, a partir de la identificación y justificación de respuestas de alumnos de Educación Primaria. Aunque en la evaluación inicial se observó un bajo razonamiento probabilístico, en la segunda los participantes fueron capaces de identificar y explicar las respuestas incorrectas de los estudiantes. Además, señala que los participantes tuvieron más éxito en el conocimiento común del contenido, teniendo un nivel de comprensión suficiente para el significado clásico de probabilidad. Sin embargo, se observó que los candidatos a profesores presentaban deficiencias en el conocimiento ampliado del contenido (HCK) y en el conocimiento especializado del contenido (SCK), y que su comprensión del enfoque frecuentista y subjetivo de la probabilidad era insuficiente.
Ortiz y Mohamend (2014) realizaron un estudio con 283 futuros profesores de educación primaria en España, en su primer año de estudios. Indican que todos habían estudiado probabilidad simple y condicional, durante la educación secundaria (dos años antes de ingresar en la universidad). Entre las dificultades encontradas señalan que existe confusión entre suceso seguro y suceso posible y la falta de razonamiento combinatorio y lograron encontrar que realizaban una interpretación errónea del experimento aleatorio, lo cual le conllevó a considerar un espacio muestral incorrecto, además que los profesores no son capaces de identificar los conceptos ocultos en una situación didáctica relacionada con la estadística o probabilidad, y que aunque fueron capaces de discriminar con facilidad las respuestas correctas e incorrectas dadas por algunos alumnos a ciertos problemas, no dejan claro el conocimiento mostrado de las posibles razones de los errores en las respuestas.
En Costa Rica se han realizado estudios referentes al conocimiento para la enseñanza de la Probabilidad con profesores de Matemática (Cuevas et al., 2018) y con futuros profesores de Matemática (Salazar, 2017; Cruz-Quesada et al., 2021).
En cuanto a estudios referentes al espacio muestral, están los realizados con estudiantes costarricenses (Hernández-Solís et al.; 2021) donde se evalúan las respuestas de 55 estudiantes costarricenses de 6º curso de educación primaria (entre 11 y 12 años), a dos tareas donde se les pide construir el espacio muestral compatible con la descripción de varios eventos, tanto en urnas y como ruletas, encontrando debilidades en la construcción de un espacio muestral que corresponda a los eventos seguro e imposible. También, (Hernández-Solís et al.; 2024) analizaron la relación entre el nivel de razonamiento proporcional y la construcción del espacio muestral en 292 estudiantes costarricenses de los cursos 6º a 10º (11-15 años); encontrando correlación entre el nivel de razonamiento proporcional y el número de espacios muestrales correctamente construidos.
4. MÉTODO
4.1. Descripción de la muestra
La muestra estuvo formada por 124 docentes en activo de las seis regiones socioeconómicas en que se divide Costa Rica, según la división regional que el Ministerio de Planificación Nacional y Política Económica (MIDEPLAN) estable para el territorio nacional. El muestreo fue por conveniencia, de acuerdo con disposición de cada Dirección Regional de Educación (DRE). Se contó con al menos una de las DRE en cada una de las regiones como se muestra en la Figura 1.
El 75% de los docentes de la muestra tiene una edad superior a 37 años, casi las dos terceras partes tiene más de 10 años de experiencia como docentes de Educación Primaria y solo 23% cuenta con menos de cinco años de experiencia; además, al consultarles por el mayor grado académico obtenido en educación, el 68,5% de la muestra respondió que licenciatura, el 21,0% maestría y solo el 10,5% posee únicamente bachillerato universitario. Por lo anterior, la muestra se caracteriza en general por docentes con grado académico suficiente para ejercer sus labores, madurez en edad y aceptable cantidad de años de experiencia en la enseñanza primaria. Además, hay un balance entre docentes graduados en universidades públicas y privadas, dividiéndose casi en partes iguales de la muestra. Todo esto hace que la información que se recolecte sea muy valiosa en relación con la formación recibida.
Figura 1
Distribución porcentual de la muestra según la división regional del MIDEPLAN.
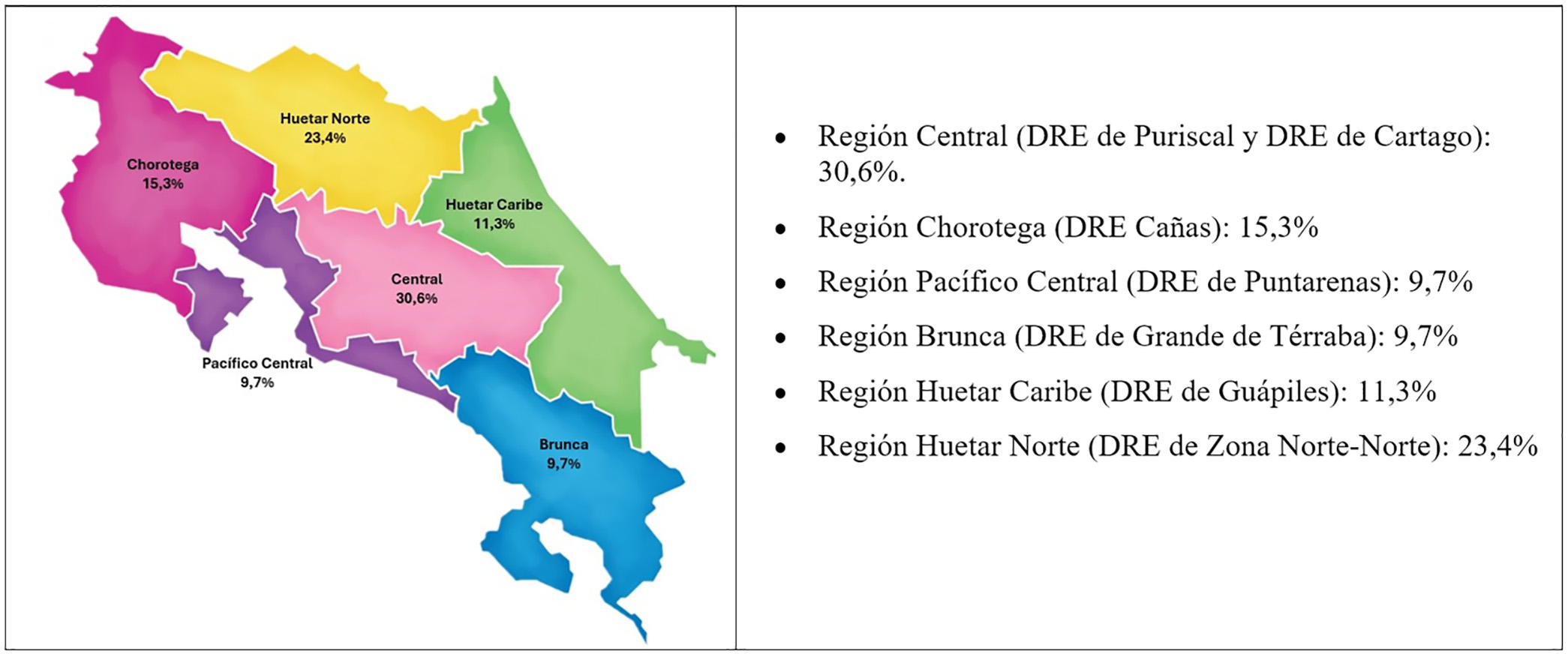
Nota: Elaboración propia.
Al preguntar a los docentes de la muestra si durante su formación profesional universitaria ¿recibió algún curso o asignatura en la cual se impartieron temas sobre Probabilidad? el 54,0% respondió que sí y el resto que no. De los docentes que respondieron que sí, el 58,2% indicó que recibió solo en un curso, y el 31,3% indicaron que en dos cursos. Al consultar por los contenidos estudiados, solo 67 docentes de la muestra respondieron (54,0%), de los que sólo 12 (17,9%) docentes indicaron haber estudiado el tema de espacios muestrales.
Por otro lado, al consultar por el nivel de satisfacción respecto a la formación profesional universitaria recibida en el tema de Probabilidad, solo el 5,7% de los docentes manifestaron estar muy satisfechos y el 16,1% estar satisfechos. Asimismo, el 44,3% manifiesta estar poco satisfecho (28,2%) o nada satisfecho (16,1%) con su formación inicial en Probabilidad. En cuanto a la pregunta, de si durante su formación profesional universitaria ¿Recibió algún curso o asignatura donde se abordará el tema de didáctica de la Probabilidad? el 73,4% respondió que no y sólo el 26,6% indicó que sí. De los docentes que respondieron que sí, el 66,7% indicó que recibió solo en un curso, y el 24,2% indicaron que en dos cursos.
4.2. Cuestionario
El instrumento está conformado por tres ítems de contenido probabilístico, que habían sido empleados en otras investigaciones y asociados a la enumeración, comprensión y construcción del espacio muestral. El propósito de tomar estos ítems fue, primero, utilizar tareas ya validadas, y segundo, poder explorar similitudes y diferencias entre los resultados obtenidos y los informados por estas investigaciones. Este cuestionario fue desarrollado para medir tres subdominios del modelo “conocimiento matemático para la enseñanza” (MKT): Conocimiento Común del Contenido (CCK), Conocimiento en el horizonte matemático (HCK) y Conocimiento del contenido y los estudiantes (KCS). A continuación, se presentan los ítems y se destacan algunos aspectos importantes.
4.2.1. Ítem 1
Fue construido por Green (1982) y utilizado por Cañizares (1997) para evaluar estrategias de enumeración en niños españoles de 10-14 años; además, lo empleó Gómez-Torres (2014) con una muestra de 157 futuros profesores de educación primaria de España.
|
ÍTEM 1. Suponga que tres niños cuyos nombres son: Andrés, Bruno y Carlos (denotados como A, B y C, respectivamente) quieren jugar por turnos con un video juego. Sortean (al azar) el orden en que van a jugar y obtienen el siguiente resultado: BCA (Es decir: Bruno juega primero, luego Carlos y por último Andrés). De acuerdo con la información anterior: a. Escriba todas las formas diferentes en que se podrían ordenar los niños para jugar. b. ¿De cuántas formas diferentes se podrían ordenar? Si llega Daniel y también desea jugar, ¿De cuántas formas diferentes se podrían ordenar los cuatro niños? |
Para resolver los apartados de este ítem, se debe comprender el concepto de permutación; es decir, que para un conjunto finito cada una de las ordenaciones posibles de los elementos es una permutación; es decir, sea el conjunto de elementos {A,B,C}, entonces el ordenamiento ABC es distinto al CAB y se deben contar como permutaciones distintas.
Además, en este caso, el tipo de permutación es sin repetición y se deben contar cada una de las permutaciones que se pueden realizar con los nombres de los niños, y para no dejar ninguna permutación de lado, se sugiere emplear alguna técnica o estrategia de conteo.
Para el apartado (a) si {A,B,C} es un conjunto de elementos donde A: Andrés, B: Bruno y C: Carlos entonces para su solución se pueden emplear las siguientes estrategias:
• Diagrama de árbol. Es una representación gráfica de los posibles resultados del experimento y para el apartado (a) del ítem 1 se podría realizar lo siguiente.
Figura 2
Diagrama de árbol del apartado (a) del ítem 1.
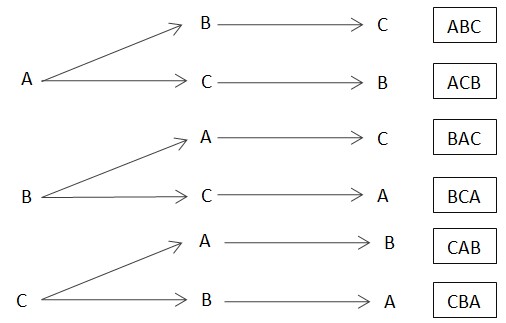
Nota: Elaboración propia.
• Enumeración sistemática. Se establece un término constante y se permutan los demás. Por ejemplo, para el apartado (a) se podría realizar lo siguiente:
Figura 3
Representación de la estrategia de enumeración sistemática.

Nota: Elaboración propia.
También, puede considerarse que como la cantidad de permutaciones es pequeña, se podría resolver mediante una enumeración no sistemática.
Respecto al apartado (b), se puede contar los elementos del espacio muestral obtenido en (a), o aplicar la fórmula de las permutaciones sin repetición n!=1∙2∙3∙∙∙n ; o sea, 3!=1∙2∙3=6.
En cuanto a la parte (c) se puede construir un diagrama de árbol o ir enlistando elementos de forma sistemática, por ejemplo, al dejar constante la A, se tiene que:
ABDC ACDB ADCB
ABCD ACBD ADBC
y luego ir cambiando el término constante.
Sin embargo, las técnicas empleadas en el apartado (a) no son muy eficientes para el (c), debido a que, al ser más elementos en el conjunto, habrá una mayor cantidad de permutaciones, por tanto, la forma más eficiente de resolverlo es mediante la fórmula de las permutaciones sin repetición, este caso es 4! = 1∙2∙3∙4=24.
4.2.2. Ítem 2
Fue tomado de Hernández-Solís et al. (2021), quienes lo aplicaron a una muestra de 55 estudiantes (27 mujeres y 28 hombres) de 6º grado de educación primaria costarricense, 40 de 11 años y 15 de 12 años.
|
ÍTEM 2. Cada una de las siguientes figuras representan cajas, y María gana cuando, sin mirar, logra sacar una bola negra. Dibuje y pinte tantas bolas negras y blancas, como consideres oportuno, para que ocurra el evento indicado en cada caso:
|
Para resolverlo primero se debe tener presente que se propone un experimento aleatorio empleando como dispositivo una caja o urna representado por un dibujo, donde cada evento se plantea de forma verbal por escrito. De acuerdo con el contexto del ítem, la única restricción es que el espacio muestral consta de bolas negras y blancas, y María gana al sacar una negra. Para cada evento, se deberá pensar en los casos favorables y los desfavorables; por ejemplo, para:
• El seguro. Se debe dibujar y pintar en la urna sólo bolas negras.
• El posible. Se puede dibujar y pintar cualquier cantidad de bolas negras y blancas, sin embargo, debe existir al menos una bola de cada color.
• El equiprobable. Se tiene que dibujar y pintar la misma cantidad de bolas negras que de blancas.
• El imposible. Se debe dibujar y pintar sólo bolar blancas.
4.2.3. Ítem 3
Fue aplicado por Gómez-Torres (2014) a 81 futuros profesores españoles y por Kurt y Coşkuntuncel (2020) a 98 futuros profesores de matemáticas.
El ítem consta de tres tareas, en los apartados (a) y (b) debe seleccionar una opción de cuatro propuestas, donde se pregunta por el evento más probable y el menos probable, respectivamente. Para responderlos correctamente se debe tener claro que en el experimento aleatorio “lanzar un dado (de seis caras) tres veces” cada lanzamiento es independiente y para poder enlistar y enumerar los resultados posibles deberá emplear alguna técnica de conteo identificando los eventos simples distinguibles.
|
ÍTEM 3. Suponga que se lanza un dado (de seis caras) tres veces. a. ¿Cuál de estos resultados es más fácil que ocurra? Marca la respuesta correcta. (A) Obtener un 5, un 2 y un 3. (B) Obtener dos veces un 5 y una vez el 3. (C) Obtener tres veces el 5. (D) Todos estos resultados son igualmente probables. b. ¿Es alguno de estos resultados menos probable que los otros dos? ¿Cuál o cuáles?
|
Las primeras dos opciones refieren a eventos compuestos y la tercera a un evento simple, donde se debe contar los resultados asociados a estos.
(A) Obtener un 5, un 2 y un 3. En este caso, se debe calcular la permutación, sin repetición, de los tres elementos: 3! = 1∙2∙3=6.
(B) Obtener dos veces un 5 y una vez el 3. Aquí se deben enumerar permutaciones con la repetición de uno de los elementos en dos ocasiones; por lo tanto, solo hay tres resultados distinguibles: (3,5,5), (5,3,5) y (5,5,3).
(C) Obtener tres veces el 5. Aquí solo habría un resultado distinguible (5,5,5).
Dado que para los tres eventos el espacio muestral es el mismo, entonces bastaría comparar la cantidad de casos favorables de cada uno. Por lo tanto, en el apartado (a) la opción A tendría la respuesta correcta y la (C) en el apartado (b).
Por otro lado, la opción (D) esta está asociada al sesgo de equiprobabilidad (Lecoutre, 1992) debido a que pueden interpretar incorrectamente la definición clásica o Laplaciana, asignando equiprobabilidad a eventos con distinta probabilidad, suponiendo que todos los eventos aleatorios son equiprobables por naturaleza sin considerar el espacio muestral.
En cuanto a la segunda tarea, el docente debe distinguir que sólo el estudiante 5 (E5) realiza una afirmación correcta, y las demás son incorrectas o parcialmente incorrectas, lo cual se argumenta a continuación:
• E1: Este argumento muestra debilidades en la comprensión de la aleatoriedad, ya que, aunque lanzar un dado es un experimento aleatorio y no se pueda predecir el resultado en cada uno de los tres lanzamientos, si se puede calcular la probabilidad mediante la definición clásica o laplaciana; es decir, se confunde la imposibilidad de predecir un resultado particular con la de conocer previamente su probabilidad, sería una forma del “enfoque en el resultado” (Konold, 1989).
• E2: Aunque responde correctamente al apartado (b), no enumera la totalidad de los casos favorables de los otros dos eventos por lo cual los considera equiprobables.
• E3: El estudiante no encuentra la totalidad de casos favorables al evento “Obtener un 5, un 2 y un 3”. Al responder que este tiene mayor probabilidad de ocurrir que los otros dos, sugiere que realizó una enumeración no sistemática y por eso no logró encontrar la totalidad de los casos en cada evento.
• E4: Aunque responde correctamente al apartado (b), no precisa que el evento “Obtener un 5, un 2 y un 3” es el más probable.
4.3. Metodología de análisis
Del modelo empleado en este estudio: conocimiento matemático para la enseñanza (MKT) (Ball et al., 2008), se evaluaron tres subdominios asociados al conocimiento de enumeración del espacio muestral, de la siguiente manera:
• Conocimiento Común del Contenido - Common Content Knowledge (CCK). Mediante el ítem 1, se analizó el conocimiento referente al razonamiento combinatorio y técnicas de conteo, y con el ítem 2, la comprensión de diferentes eventos mediante la construcción del espacio muestral.
• Conocimiento en el horizonte matemático - Horizon Content Knowledge (HCK). Este se analizó mediante los apartados (a) y (b) del ítem 3, donde se debe enumerar los resultados elementales de tres eventos compuestos y poder así comparar sus probabilidades. Aquí también se podía investigar si está presente en los docentes el sesgo de equiprobabilidad (Lecoutre, 1992).
• Conocimiento del contenido y los estudiantes - Knowledge of Content and Students (KCS). Para evaluar el conocimiento del docente en cuanto a los errores comunes en el estudiantado, se utilizó el apartado (c) del ítem 3. Dado que el docente debe evaluar cinco respuestas ficticias de estudiantes e indicar cuál o cuáles son correctas y cuáles no, lo cual involucra por parte del docente el conocimiento de estrategias o argumentos correctos y también el relacionado con concepciones erradas. Esto a su vez, permitió no sólo se evaluar si se distinguen los errores de enumeración, sino también el sesgo de equiprobabilidad (Lecoutre, 1992) y “enfoque en el resultado” (Konold, 1989).
5. RESULTADOS
En la Tabla 2 se muestran los resultados obtenidos, según lo indicado por las personas docentes de la muestra, respecto a cómo se podrían ordenar los tres niños para jugar (apartado a) de acuerdo con el contexto del ítem 1. Se destaca que el 62,1% determinó la cantidad correcta de formas y el 30,6% encontró menos de las seis formas diferentes de ordenamiento. Solo ocho personas docentes determinaron más de seis formas y un único docente no respondió el ítem.
Tabla 2
Frecuencia y porcentaje de respuestas dadas por los docentes de la muestra en la parte (a) del ítem 1 relacionado con enumeración del espacio muestral
|
Número de elementos en la lista |
Frecuencia |
Porcentaje |
|
Menor que 6 |
38 |
30,6 |
|
6 (correcta) |
77 |
62,1 |
|
Mayor que 6 |
8 |
6,5 |
|
No responde |
1 |
0,8 |
Los resultados obtenidos son inferiores a los conseguidos en Gómez-Torres (2014), donde el 93,6% de futuros docentes españoles contestaron correctamente a este apartado.
Tabla 3
Frecuencia y porcentaje de respuestas dadas por los docentes de la Muestra en la parte (b) del ítem 1
|
Número de elementos en la lista |
Frecuencia |
Porcentaje |
|
Menor que 6 |
34 |
27,4 |
|
6 (correcta) |
77 |
62,1 |
|
Mayor que 6 |
10 |
8,1 |
|
No responde |
3 |
2,4 |
En cuanto a la parte (b) del ítem 1 se pide indicar la cantidad de formas diferentes en que se podrían ordenar los niños para jugar; es decir, cuantificar la parte (a) del ítem. Sobresale, que coinciden los porcentajes de respuestas correctas, no así las respuestas incorrectas, que difieren un poco; además, que tres personas docentes no responden a la pregunta planteada. En la Tabla 3 se resume la información obtenida.
Debido a los resultados obtenidos en las Tablas 2 y 3 se quiso revisar si había coincidencias entre el apartado (a) y el (b) del ítem, por lo que en la Tabla 4 se muestra que 74 personas docentes (59,7%) respondieron correctamente en ambas partes; siendo un poco inferiores a los obtenidos por Green (1982), con estudiantes ingleses y a los de Cañizares (1997) con estudiantes españoles, 81% y 74 % respectivamente. Solo 11 docentes no concordaron en ambos apartados del ejercicio, de los cuales tres tuvieron alguna de ellas correctamente, concordando con el porcentaje obtenido (5,1%) en Gómez-Torres (2014) con futuros profesores.
Tabla 4
Coincidencia entre partes a y b en el ítem 1
|
Coincidencia |
Frecuencia |
Porcentaje |
|
Sí (con respuesta correcta) |
74 |
59,7 |
|
Sí (con respuesta incorrecta) |
39 |
31,5 |
|
No |
11 |
8,5 |
En la Tabla 5 se muestra la distribución de las respuestas de los docentes al apartado (c), donde se aprecia que sólo 17 docentes pudieron cuantificar correctamente la cantidad de formas diferentes en que se podrían ordenar los cuatro niños para jugar. De esto se puede inferir que las estrategias utilizadas no fueron eficientes para la cantidad de elementos del conjunto. De hecho, más del 80% contabiliza menos de 24 elementos de la lista.
Tabla 5
Frecuencia y porcentaje de respuestas en la parte (c) del ítem 1
|
Número de elementos en la lista |
Frecuencia |
Porcentaje |
|
Menor que 24 |
100 |
80,6 |
|
24 (correcta) |
17 |
13,7 |
|
Mayor que 24 |
6 |
4,8 |
|
No responde |
1 |
0,9 |
En este apartado se obtienen mejores resultados en Gómez-Torres (2014), donde poco más de la mitad de los futuros profesores respondió en forma correcta. Ahora, al comparar con los estudios realizados por Green (1982) y Cañizares (1997), con niños de 10-14 años, los resultados fueron similares, 15% en ambos casos.
A partir de lo evidenciado en las Tablas 2, 3 y 4, era necesario analizar las estrategias empleadas por las personas docentes en las partes a y c, lo cual se realiza en la Tabla 6; donde sobresale que la más empleada fue enlistar elementos de manera no sistemática, el 74,2% la utiliza en la parte (a) y el 41,9% en la (c). Esta disminución en el porcentaje se debe a que en la parte (c) es poco eficiente realizarla debido al aumento de la cantidad de permutaciones, esto hace que el 26,6% decida no mostrar ninguna estrategia en la parte (c) o utilizar alguna otra. Para este ítem (en especial en la parte c), las más eficientes serían la fórmula de permutación, listado sistemático, diagrama de árbol y regla del producto; sin embargo, estas fueron utilizadas con poca frecuencia (menor a 30%), siendo las listas sistemáticas las más frecuentes (23,4%).
En Gómez-Torres (2014) respecto a los apartados (a) y (b) del ítem, lo más frecuente fue el uso de una lista (parcialmente sistemática, seguida de la sistemática); mientras que en la parte (c) lo más frecuente fue la regla del producto, seguido de la enumeración parcialmente sistemática.
Es claro que el apartado (c) tiene mayor complejidad que (a) y (b), debido al aumento de los elementos por permutar. Esta complejidad puede deberse a que ningún docente empleó la fórmula de permutación lo cual conlleva a considerar que estos conocimientos deberían reforzarse en los docentes.
Tabla 6
Distribución de estrategias empleadas por las personas docentes de la muestra en la parte a y c del ítem 1
|
Estrategia |
Parte a |
Parte c |
||
|
Frecuencia |
Porcentaje |
Frecuencia |
Porcentaje |
|
|
Fórmula de permutación |
- |
0,0 |
- |
0,0 |
|
Regla del producto |
2 |
1,6 |
6 |
4,8 |
|
Diagrama de árbol o algún esquema gráfico |
- |
0,0 |
1 |
0,8 |
|
Lista sistemática |
25 |
20,2 |
29 |
23,4 |
|
Listas no sistemáticas |
92 |
74,2 |
52 |
41,9 |
|
Estrategias minoritarias |
4 |
3,2 |
3 |
2,4 |
|
No realiza estrategia |
1 |
0,8 |
33 |
26,6 |
En la Tabla 7 se muestra la distribución de los espacios muestrales construidos por los participantes de acuerdo con el evento solicitado en el ítem 2. Se puede apreciar que no existen grandes dificultades para construir los eventos posible y equiprobable, obteniendo porcentajes de corrección que rondan el 95%; sin embargo, aproximadamente solo las dos terceras partes de la muestra, construye correctamente el suceso seguro (68,5%) y el suceso imposible (66,9%), confundiéndolos con el suceso muy probable (19,4%) y poco probable (23,5%), respectivamente.
Tabla 7
Porcentaje de espacios muestrales construidos por las personas docentes de acuerdo con los eventos solicitados en el ítem 2
|
Espacio muestral construido |
Tipo de suceso pedido |
|||
|
Seguro |
Posible |
Equiprobable |
Imposible |
|
|
Corresponde al suceso seguro |
68,5 |
2,4 |
1,6 |
0,8 |
|
Corresponde a un suceso muy probable |
19,4 |
37,9 |
- |
1,6 |
|
Corresponde a un suceso equiprobable |
0,8 |
8,9 |
94,4 |
3,2 |
|
Corresponde a suceso posible |
7,3 |
44,4 |
3,2 |
2,4 |
|
Corresponde a un suceso poco probable |
1,6 |
4,0 |
0,8 |
23,5 |
|
Corresponde a un suceso imposible |
1,6 |
1,6 |
- |
66,9 |
|
No construye |
0,8 |
0,8 |
- |
1,6 |
Nota: se subrayan los porcentajes de sucesos correctamente construidos según el suceso pedido.
Se obtuvieron mejores resultados que los logrados en el estudio de Hernández-Solís et al. (2021) con estudiantes de sexto año de educación primaria costarricense, donde sólo el 34,5% construyeron el evento seguro y 25,5% el suceso imposible. Sin embargo, hay que resaltar que la tercera parte de la muestra de docentes tienen dificultades con los conceptos de evento seguro y evento imposible, y estos errores pueden ser transmitidos a los estudiantes.
En la Tabla 8 se presenta la distribución de las respuestas al apartado (a) del ítem 3; donde sobresale que menos del 20% selecciona la opción correcta y las dos terceras partes de la muestra consideran que todos los resultados son igualmente probables; esto revela no solo grandes debilidades en técnicas de conteo, al no identificar resultados simples distinguibles, por ejemplo diferenciar entre 523 y 532; sino también revela la presencia del sesgo de equiprobabilidad (Lecoutre, 1992) en las dos terceras partes de la muestra de docentes.
Tabla 8
Frecuencia y porcentaje de respuestas del apartado a) en el ítem 3. Espacio muestral y las probabilidades (sesgo de equiprobabilidad)
|
Respuesta |
Frecuencia |
Porcentaje |
|
Obtener un 5, un 2 y un 3 (Correcta) |
23 |
18,6 |
|
Obtener dos veces un 5 y una vez el 3 |
0 |
0,0 |
|
Obtener tres veces el 5 |
0 |
0,0 |
|
Todos estos resultados son igualmente probables |
83 |
66,9 |
|
No responde |
18 |
14,5 |
En la Tabla 9 se presenta la distribución de las respuestas al apartado (b) del ítem 3; donde aparece una consistencia con los resultados obtenidos en la Tabla 8, solo que aumentó el porcentaje de personas docentes que no respondieron a la pregunta. Lo anterior reafirma las debilidades en el conteo de resultados.
Tabla 9
Frecuencia y porcentaje de respuestas del apartado b) en el ítem 3. Espacio muestral y las probabilidades (sesgo de equiprobabilidad)
|
Respuesta |
Frecuencia |
Porcentaje |
|
Obtener un 5, un 2 y un 3 |
2 |
1,6 |
|
Obtener dos veces un 5 y una vez el 3 |
1 |
0,8 |
|
Obtener tres veces el 5 (Correcta) |
28 |
22,6 |
|
Eligió dos eventos |
7 |
5,6 |
|
Todos estos resultados son igualmente probables |
46 |
37,1 |
|
No responde |
40 |
32,3 |
En la Tabla 10 se puede apreciar que solo el 10,5% tuvo las dos respuestas correctas en los apartados (a) y (b), resultado que es inferior al obtenido Gómez-Torres (2014), donde el 27,4% de los futuros profesores españoles respondió correctamente ambas partes. Por otro lado, el 32,3% de la muestra contestó, en los dos apartados, que los resultados son igualmente probables; es decir, que evidencian el sesgo de equiprobabilidad; en cambio en Gómez-Torres (2014) el porcentaje fue mayor 49,0%, es decir, casi la mitad de la muestra presentó el sesgo de equiprobabilidad (Lecoutre, 1992).
Tabla 10
Porcentaje de respuestas en los apartados a) y b) en el ítem 3. Espacio muestral y las probabilidades (sesgo de equiprobabilidad)
|
Apartado (a) |
Apartado (b) |
|||||
|
NR |
A |
B |
C |
D |
Elige dos eventos |
|
|
A |
3,2 |
0,0 |
0,8 |
10,5 |
2,4 |
1,6 |
|
D |
21,0 |
1,6 |
0,0 |
9,7 |
32,3 |
2,4 |
|
NR |
8,1 |
0,0 |
0,0 |
2,4 |
2,4 |
1,6 |
En el apartado (c) de este ítem se brindó varios argumentos ficticios de posibles respuestas que darían algunas personas estudiantes y cada persona docente debía analizarlos e indicar si eran correctos o incorrectos. En la Tabla 11, se muestra la frecuencia y porcentajes de los argumentos elegidos como correctos e incorrectos; debe considerarse que en ese caso son correctos sólo los argumentos E4 y E5. De la información recolectada se destaca que el 58,9% de docentes considera que el argumento E1 es correcto, lo cual es consistente con los resultados obtenidos en las Tablas 8 y 9. Asimismo, sobresalen los porcentajes bajos en los argumentos correctos E4 (12,1%) y E5 (18,5%), considerándolos incorrectos el 71,8% y 63,8% de la muestra, respectivamente. El porcentaje de docentes que no seleccionan argumentos se mantiene con poca variabilidad de entre 15,3% a 17,7%.
Tabla 11
Frecuencia y porcentaje de selección de argumentos de estudiantes que el docente considera como correctos e incorrectos en el ítem 3
|
Argumento de estudiante |
Correctas |
Incorrectas |
No selecciona |
|||
|
Frecuencia |
Porcentaje |
Frecuencia |
Porcentaje |
Frecuencia |
Porcentaje |
|
|
E1 |
73 |
58,9 |
32 |
25,8 |
19 |
15,3 |
|
E2 |
16 |
12,9 |
88 |
71,0 |
20 |
16,1 |
|
E3 |
23 |
18,5 |
82 |
66,1 |
19 |
15,4 |
|
E4 (correcto) |
15 |
12,1 |
89 |
71,8 |
20 |
16,1 |
|
E5 (correcto) |
23 |
18,5 |
79 |
63,8 |
22 |
17,7 |
En el estudio de Gómez-Torres (2014), se obtuvieron mejores resultados, ya que el 90% de los futuros docentes de primaria consideró E5 como correcto y el 60% marcó E4 como correcto y el 27,5% como parcialmente correcto. De los argumentos incorrectos, en Gómez-Torres (2014) solo dos docentes marcaron como correcto E1 y ninguno a E2, a diferencia que en nuestro estudio más de la mitad de la muestra de docentes consideró como correcto E1 y 12,9% el argumento E2. En cuanto a E3 el 66,1% de la muestra de docentes lo consideró incorrecto, en cambio en Gómez-Torres (2014) solo el 45% lo consideró incorrecto.
Considerando las Tablas 8, 9 y 11 se puede notar que hay una fuerte debilidad en lo que respecta a los conocimientos básicos de conteo y la distinción de resultados distinguibles en un experimento aleatorio; además, que un alto porcentaje de los docentes presenta el sesgo de equiprobabilidad (Lecoutre, 1992).
6. DISCUSIÓN Y CONCLUSIONES
En este trabajo se evaluaron los subdominios CCK, HCK, SCK del modelo MKT (Ball et al. 2008), referentes al contenido matemático de espacios muestrales, donde específicamente se analizaron las respuestas y argumentos de 124 docentes de Educación Primaria en ejercicio, en ítems donde se debía enumerar y construir espacios muestrales asociados a diferentes eventos simples y compuestos. Estos resultados obtenidos brindarán información valiosa a formadores de docentes en relación con los conocimientos matemáticos y didácticos que necesitan los docentes de Educación Primaria para enseñar probabilidad.
De acuerdo, a los resultados obtenidos se evidencian debilidades en los tres subdominios analizados:
• Sobre el CCK y el HCK: se muestran debilidades en la enumeración de diferentes espacios muestrales, asociados a poco conocimiento de técnicas de conteo, centrándose en estrategias no sistemáticas que solo tuvieron respuestas correctas cuando la cantidad de elementos que había que permutar eran pocos (3) pero se les dificulta cuando se aumentan elementos (4). Esta debilidad afecta la visualización correcta de espacios muestrales y eventos, por ende, al cálculo de probabilidades, por ejemplo, en el ítem 3, menos de la cuarta parte de la muestra respondió correctamente.
En cuanto a la construcción de espacios muestrales, al igual que en estudios con estudiantes (e.g. Cañizares,1997; Green, 1982; Hernández-Solís et al., 2021 y Hernández-Solís et al., 2024) no existen grandes dificultades para construir los eventos posibles y equiprobables, pero sí en el evento seguro y el evento imposible, confundiéndolos con el evento muy probable y poco probable, respectivamente. Esto hace pensar que existen debilidades en la comprensión del concepto de experimento aleatorio y los axiomas básicos de probabilidad.
• Sobre el SCK: en el análisis de didáctico de respuestas ficticias de estudiantes, casi las tres cuartas partes de la muestra indicó como incorrecta la única respuesta correcta, señalando respuestas incorrectas como correctas. Este mismo ítem, indica que gran parte de la muestra evidencia el sesgo de equiprobabilidad (Lecoutre, 1992).
Lo anterior debe ser analizado y valorado por quienes tienen a cargo la responsabilidad de formar docentes de I y II Ciclo, así como responsables de capacitación y formación continua, dado que existen debilidades que deben ser atendidas, para garantizar que al final de la Educación Primaria el estudiantado identifique distintos eventos (más probables, menos probables o igualmente probables) de acuerdo con el número de resultados simples de cada uno de estos (MEP, 2012); por lo que, el conocimiento en espacios muestrales y técnicas de conteo se vuelven fundamentales para la labor docente. En este sentido, las distintas investigaciones coinciden en la importancia de mejorar la formación para potenciar el desarrollo profesional del profesorado de matemáticas en la enseñanza de la probabilidad (Franco y Alsina, 2022). Sin embargo, Alpízar-Vargas y Alfaro-Arce (2019) señalan que la cantidad de cursos de matemáticas es muy limitada en los programas de formación de docentes para la educación primaria en Costa Rica, hacen necesaria una mejora en los programas de capacitación y actualización, para solventar las debilidades en la formación universitaria inicial.
En cuanto a la didáctica de probabilidad, se considera necesario desarrollar procesos de capacitación contínua centrados no sólo en el conocimiento matemático, sino también en los errores comunes, creencias y sesgos que presentan los estudiantes en la resolución de tareas probabilísticas. Esto se puede lograr mediante el análisis respuestas dadas por el estudiante o ficticias, que apoyen y favorezcan los procesos de enseñanza y aprendizaje de la probabilidad.
REFERENCIAS BIBLIOGRÁFICAS
Alonso-Castaño, M., Alonso, P., Mellone, M. y Rodríguez-Muñiz, L.J. (2021). What mathematical knowledge do prospective teachers reveal when creating and solving a probability problem? Mathematics, 9(24), 3300. https://doi.org/10.3390/math9243300
Alpízar, M. y Alfaro, A. (2019). La formación universitaria de docentes de educación primaria: el caso de matemáticas. Uniciencia, 33(2), 110-154. http://dx.doi.org/10.15359/ru.33-2.8
Alpízar, M., Barrantes, J., Bolaños, H., Céspedes, M., Delgado, E., Freer, D., Padilla, E. y Víquez, M. (2012). Aspectos relevantes sobre la formación docente en I y II ciclos en los temas probabilidad y estadística. Educare, 16(2), 113-129. https://doi.org/10.15359/ree.16-2.7
Alpízar, M., Chavarría, L. y Oviedo, K. (2015). Percepción de un grupo de docentes de I y II ciclo de educación general básica de escuelas públicas de Heredia sobre los temas de estadística y probabilidad. Actualidades Investigativas en Educación, 15(1), 1-23. https://doi.org/10.15517/aie.v15i1.17728
Alsina, Á. (2017). Contextos y propuestas para la enseñanza de la estadística y la probabilidad en Educación Infantil: un itinerario didáctico. Épsilon, 95, 25-48.
Ball, D., Thames, M. y Phelps, G. (2008). Content knowledge for teaching what makes it special? Journal of Teacher Education, 59(5), 389-407. https://doi.org/10.1177/0022487108324554
Batanero, C., Álvarez-Arroyo, R. Hernández-Solís-Solís, L. y Gea, M.M. (2021). El inicio del razonamiento probabilístico. PNA, 15(4), 267-288. https://doi.org/10.30827/pna.v15i4.22349
Batanero, C., Gea, M.M. y Álvarez-Arroyo, R. (2023). Educação do raciocínio probabilístico. Educação Matemática Pesquisa, 25(2), 127-144. https://doi.org/10.23925/1983-3156.2023v25i2p127-144
Cañizares, M.J. (1997). Influencia del razonamiento proporcional y combinatorio y de creencias subjetivas en las intuiciones probabilísticas primarias. [Tesis Doctoral, Universidad de Granada].
Carrillo, J., Climent, N., Contreras, L.C. y Muñoz-Catalán, M.C. (2013). Determining specialised knowledge for mathematics teaching. En B. Ubuz, C. Hasery M. Mariotti (Eds.), Proceedings of the CERME 8 (pp. 2985-2994). ERME.
Cruz-Quesada, J., Alfaro-Carvajal, C. y Guillen-Oviedo, H. (2021). Conocimiento especializado de profesores de matemática en formación inicial sobre la noción clásica de probabilidad. En J.G. Moriel-Junior (Ed.), Actas del V Congreso Iberoamericano sobre conocimiento especializado del profesor de Matemáticas (pp. 216-223). Congresseme.
Cuevas, H., y Ramírez, G. (2018). Desempeño en estocástica entre profesores de educación secundaria: un estudio exploratorio en dos regiones de Costa Rica y México. Educación Matemática, 30(1), 93-132. https://doi.org/10.24844/EM3001.04
Escudero, D.I., Carrillo, J., Flores-Medrano, E., Climent, N., Contreras, L.C. y Montes, M. (2015). El conocimiento especializado del profesor de matemáticas detectado en la resolución del problema de las cuerdas. PNA, 10(1), 53-77.
Franco, J. y Alsina, A. (2022). El conocimiento del profesorado de Educación Primaria para enseñar estadística y probabilidad: una revisión sistemática. Aula Abierta, 51(1), 7-16. https://doi.org/10.17811/rifie.51.1.2022.7-16
Godino, J., Giacomone, B., Batanero, C. y Font, V. (2017). Enfoque Ontosemiótico de los Conocimientos y Competencias del Profesor de Matemáticas. Bolema, 31(57), 90-113. http://dx.doi.org/10.1590/1980-4415v31n57a05
Gómez-Torres, E. (2014). Evaluación y desarrollo del conocimiento matemático para la enseñanza de la probabilidad en futuros profesores de Educación Primaria. [Tesis doctoral, Universidad de Granada]. http://hdl.handle.net/10481/34020
Green, D.R. (1982). Probability concepts in school pupils aged 11-16 years. [Ph. Dissertation, University of Loughborough].
Grossman, P. (1990). The Making of a Teacher. Teacher Knowledge and Teacher Education. Columbia University.
Hernández-Solís, L.A., Batanero, C., Gea, M.M. y Álvarez-Arroyo, R. (2021). Construcción de espacios muestrales asociados a distintos tipos de sucesos: Un estudio exploratorio con niños de educación primaria. Educación Matemática, 33(1), 181-207. http://dx.doi.org/10.24844/EM3301.07
Hernández-Solís, L.A., Batanero, C. y Gea, M.M. (2024). Razonamiento proporcional y construcción de espacios muestrales asociados a distintos tipos de sucesos por estudiantes costarricenses. Revista de Educación Estadística, 3, 1-28. https://doi.org/10.29035/redes.3.1.1
Hill, H., Ball, D. y Schilling, S. (2008). Unpacking pedagogical content knowledge: conceptualizing and measuring teachers’ topic-specific knowledge of students. Journal for Research in Mathematics Education, 39(4), 372-400.
Jones, G., Langrall, C. y Mooney, E. (2007). Research in probability: responding to classroom realities. En F. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp. 909-955). Information Age Publishing y NCTM.
Konold, C. (1989). Informal conceptions of probability. Cognition and Instruction, 6(1), 59-98. https://doi.org/10.1207/s1532690xci0601_3
Kurt, G. y Coşkuntuncel, O. (2020). Assessment of elementary mathematics teachers’ probability content knowledge in terms of different meanings of probability. Turkish Journal of Computer and Mathematics Education, 11(3), 706-732.
Lecoutre, M.P. (1992). Cognitive models and problem spaces in “purely random” situations. Educational Studies in Mathematics, 23, 557-568. https://doi.org/10.1007/BF00540060
Lima, E. y Borba, R. (2021). Articulando combinatória e probabilidade: jovens e adultos revisitando problemas combinatórios via construção de espaços amostrais. Paradigma, 42(Extra 1), 257-284. https://doi.org/10.37618/PARADIGMA.1011-2251.2021.p257-284.id1025
MEP (2012). Programas de Estudio de Matemáticas. I, II Y III Ciclos de la Educación General Básica y Ciclo Diversificado. Ministerio de Educación Pública.
Nilsson, P. y Li, J. (2015). Teaching and learning of probability. En S.J. Cho (Ed.), Proceedings of the 12th International Congress on Mathematical Education: Intellectual and Attitudinal Challenges (pp. 437-442). Springer.
Nunes, T., Bryant, P., Evans, D., Gottardis, L. y Terlektsi, M.-E. (2014). The cognitive demands of understanding the sample space. ZDM Mathematics Education, 46(3), 437-448. https://doi.org/10.1007/s11858-014-0581-3
OECD (2023). PISA 2022 Assessment and Analytical Framework. OECD Publishing. https://doi.org/10.1787/dfe0bf9c-en
Ortíz, J.J. y Mohamend, N. (2014). Conocimiento de futuros profesores sobre espacio muestral. Quadrante, 23(2), 5-22. https://quadrante.apm.pt/article/view/22910/16976
Pino, G. y Estrella, S. (2012). Educación estadística: relaciones con la matemática. Pensamiento Educativo. Revista de Investigación Educacional Latinoamericana, 49(1), 53-64.
Rodríguez-Alveal, F., Díaz-Levicoy, D. y Vásquez, C. (2018). Evaluación de la alfabetización probabilística del profesorado en formación y en activo. Estudios Pedagógicos, 44(1), 135-156. http://dx.doi.org/10.4067/S0718-07052018000100135
Salazar, L. (2017). Invención de problemas contextualizados de probabilidad: una competencia a desarrollar en profesores de matemática. Comunicación, 26(2), 38-48. https://dx.doi.org/10.18845/rc.v26i2-17.3443
Shulman, L. (1986). Those who understand: knowledge growth in teaching. Educational Researcher, 15(2), 4-14.
Shulman, L. (1987). Knowledge and teaching: foundations of the new reform Harvard Educational Review, 57(1), 1-22.
Vásquez, C. y Alsina, Á. (2017). Aproximación al conocimiento común del contenido para enseñar probabilidad desde el modelo del conocimiento didáctico-matemático. Educación Matemática, 29(3), 79-108. https://doi.org/10.24844/EM2903.03
Vásquez, C. y Alsina, A. (2019). Intuitive ideas about chance and probability in children from 4 to 6 years old. Acta Scientiae, 21(3), 131-154. https://doi.org/10.17648/acta.scientiae.v21iss3id5215
Vásquez, C. y Alsina, Á. (2021). Analysing probability teaching practices in Primary Education: What tasks do teachers implement? Mathematics, 9(19), 2493. https://doi.org/10.3390/math9192493
Como citar:
Hernández-Solís, L.A., Quesada-Fernández, C. y Padilla-Mora, E. (2025). Caracterización del conocimiento matemático para la enseñanza de espacios muestrales en docentes de Educación Primaria costarricense. Revista de Educación Estadística, 4, 1-25. https://doi.org/10.29035/redes.4.1.2

Esta obra está bajo una licencia de Creative Commons
Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional.
1 *Autor de correspondencia: lhernandez@uned.ac.cr (L. Hernández-Solís)
https://orcid.org/0000-0003-2956-8102 (lhernandez@uned.ac.cr).
2 https://orcid.org/0000-0002-9592-6927 (cquesadaf@uned.ac.cr).
3 https://orcid.org/0009-0002-9517-0418 (epadilla@uned.ac.cr).

