|
|
Revista de Educación Estadística Vol. 4, pp. 1-25, ene. 2025 - dic. 2025 ISSN 2810-6164 |
DOI: https://doi.org/10.29035/redes.4.1.3
EL PAPEL DEL SENTIDO ESTOCÁSTICO EN LA EDUCACIÓN EN LA CIENCIA DE DATOS
O papel do sentido estocástico no ensino da ciência dos dados
The role of stochastic sense in the Data Science Education
Ana Serradó Bayés1
Colegio La Salle-Buen Consejo (Puerto Real, España)
María Lucia Vargas2
Colegio La Salle-Buen Consejo (Puerto Real, España)
Resumen
La educación en la ciencia de datos contempla la integración de las matemáticas, las ciencias de la computación y los conocimientos sustantivos. La revisión de la literatura ha permitido identificar tres enfoques organizativos para los conocimientos matemáticos y estadísticos, cada uno asociado a diferentes conceptualizaciones del sentido: el estadístico, el probabilístico y el estocástico. Con el objetivo de establecer el papel del sentido estocástico en la educación en ciencia de datos y responder a las preguntas de investigación sobre las organizaciones fenomenológicas del sentido estocástico y las grandes ideas que estructuran dicha educación en el contexto español, se ha analizado el currículum escolar legislado en España para las etapas educativas comprendidas entre los 6 y los 18 años. Los resultados del análisis muestran que el sentido estocástico desempeña un papel predominante, al constituirse como una herramienta fundamental para la resolución de problemas basados en datos, que emergen en los contextos disciplinares de los conocimientos sustantivos y se automatizan mediante los saberes propios de la computación. Esta organización interdisciplinar facilita la construcción de puentes entre los conocimientos y capacidades que definen el sentido estocástico y los principios de la ciencia de datos, bajo una perspectiva centrada en la cultura generativa y predictiva de la modelización de datos.
Palabras clave: Educación Estadística, Ciencia de Datos, Currículo, Análisis de Contenido.
Resumo
O ensino da ciência dos dados prevê a integração da matemática, da informática e do conhecimento substantivo. A revisão da literatura identificou três abordagens organizacionais da literacia matemática e estatística, cada uma delas associada a diferentes conceptualizações de sentido: estatística, probabilística e estocástica. Para estabelecer o papel do sentido estocástico na educação para a ciência dos dados e para responder às questões de investigação sobre as organizações fenomenológicas do sentido estocástico e as grandes ideias que estruturam essa educação no contexto espanhol, foi analisado o currículo escolar legislado em Espanha para as etapas educativas entre os 6 e os 18 anos de idade. Os resultados da análise mostram que o sentido estocástico desempenha um papel predominante, pois constitui uma ferramenta fundamental para a resolução de problemas baseados em dados, que emergem nos contextos disciplinares do conhecimento substantivo e são automatizados através do conhecimento da computação. Esta organização interdisciplinar facilita a construção de pontes entre os conhecimentos e capacidades que definem o sentido estocástico e os princípios da ciência dos dados, numa perspetiva centrada na cultura generativa e preditiva da modelação de dados.
Palavras-chave: Educação Estatística, Ciência dos Dados, Currículo, Análise de Conteúdo.
Abstract
Data science education envisages the integration of mathematics, computer science and substantive knowledge. The literature review has identified three organizational approaches to mathematical and statistical literacy, each associated with different conceptualizations of meaning: statistical, probabilistic and stochastic. In order to stablish the role of stochastic sense in data science education and to answer the research questions about phenomenological organizations of stochastic sense and the big ideas that structure such education in the Spanish context, the school curriculum legislated in Spain for the educational stages between 6 and 18 years old has been analyzed. The results of the analysis show that the stochastic sense plays a predominant role, as it constitutes a fundamental tool for the resolution of data-based problems, which emerge in the disciplinary contexts of substantive knowledge and are automated by means of the knowledge of computation. This interdisciplinarity organization of the curriculum facilitates the building of bridges between the knowledge and capabilities that define the stochastic sense and the principles of data science, under a perspective centred on the generative and predictive culture of data modelling.
Keywords: Statistical education, Data Science, Curriculum, Content Analysis.
Recibido: 15/07/2025 - Aceptado: 13/05/2025
1. INTRODUCCIÓN
En el año 1962, J.W. Tukey escribía el ensayo El futuro del análisis de datos, donde ponía el punto de mira del estadista en el análisis de datos frente a las propuestas de estadística inferencial que se había puesto en boga (Tukey, 1962). Cuatro décadas más tarde W.S. Cleveland retomaba estas ideas y presentaba un plan de acción para expandir la estadística hacia las áreas técnicas. Este plan ambicioso implicaba un cambio sustancial en la estadística, germinándose así la llamada “ciencia de los datos” (Cleveland, 2001). En su trabajo determinaba que el científico de datos se enfrentaba a dos tareas críticas: (1) la especificación, consistente en la construcción de un modelo para los datos, y (2) la estimación y el estudio de la distribución a partir de la realización de inferencias formales, matemático-probabilísticas, condicionadas al modelo obtenido a partir del uso de la informática. Esta propuesta le permitía argumentar sobre la bidireccionalidad a la hora de aplicar los conocimientos en ambas materias, la estadística y la tecnología; y las limitaciones a la hora de aplicar el conocimiento sobre el análisis de datos que tenían los informáticos al igual que los estadistas al uso de los entornos informáticos. En conclusión, la visión sobre la ciencia de datos que presentaba Cleveland (2001) integraba la estadística, la modelización matemático-probabilística y el uso de la tecnología.
Una década más tarde, Conway (2010) argumentaba la insuficiencia de estos campos de estudio a la hora de caracterizar la ciencia de datos, e indicaba que la ciencia de datos se encuentra en la intersección de tres elementos constitutivos: las matemáticas y la estadística, las competencias o conocimientos sustantivos y la computación conjuntamente con el tratamiento de datos. Finzer (2013), aportándole una visión pedagógica a esta caracterización de la ciencia de datos, argumentaba que los conocimientos estadísticos favorecen la comprensión de la variabilidad, y los conocimientos sustantivos son los campos de donde surgen los problemas y el conjunto de datos a analizar.
Posteriormente, Engel (2017) contemplaba esta visión procedimental y práctica de la ciencia de datos al definirla como: “un conjunto de habilidades y técnicas que incluyen la estadística, la informática (codificación, visualización, computación de datos, aprendizaje automático, etc.), las matemáticas y la experiencia en el área temática de la que proceden los datos” (p. 1).
Pero no es hasta 2019, cuando Yan y Davis ante la falta de consenso acerca de una definición sobre que es la ciencia de datos, la definen como:
La ciencia del aprendizaje de los datos: una disciplina que proporciona teoría, metodología, principios y directrices para el análisis de datos en busca de herramientas o conocimientos. Entre las herramientas se incluyen aquellas que pueden ayudar al usuario a realizar un mejor análisis, como las herramientas de visualización, recopilación o exploración de datos, y el valor se refiere principalmente a aquellas con valor comercial o científico (Yan y Davis, 2019, p. 99).
En su artículo, estos autores valoran como los planes de estudios difieren de una institución a otra debido a los distintos niveles de experiencia del profesorado y a las diferentes disciplinas que se desarrollan. Además, sugieren poner el foco de atención de la investigación en las propuestas curriculares en la ciencia de datos. Desde el año 2022 se han incrementado las propuestas curriculares en ciencia de datos en edades escolares. En varios estados de Estados Unidos, se han creado materias optativas de ciencia de datos (Drozda et al., 2022). Asimismo, en Australia, Canada, Inglaterra, Alemania, Holanda, Nueva Zelanda y Estados Unidos, el proyecto International Data Science in Schools Project (IDSSP Curriculum Team, 2019) se centra en cómo aprender de los datos en los dos últimos años de la escolarización pre-universitaria. La ciencia de datos es un nuevo componente en el currículum de Canadá y el pensamiento computacional se encuentra en los estándares de Australia y en el currículo de Cataluña (Burril, 2023).
En el contexto español, la CEMat (2021) establecía las bases para la elaboración de un currículo de Matemáticas en Educación no Universitaria donde adoptaba la noción de sentido matemático y lo situaba como elemento central que organiza la enseñanza del conocimiento matemático. En este documento se caracteriza, entre otros, el sentido estocástico como el sentido de los contenidos matemáticos escolares que proporciona una organización fenomenológica del contenido. En consonancia, se establece que los sentidos matemáticos escolares son los conjuntos de capacidades generales que enlazan los elementos del contenido matemático con aspectos cognitivos de su aprendizaje y con la noción de competencia matemática (Ruiz-Hidalgo y Flores, 2022). Además, de estos cambios en la organización del currículo, Rodríguez-Muñiz (2023) argumentaba que el avance hacia la ciencia de datos necesita de cambios metodológicos en el currículum y se cuestionaba si debe cambiar la forma en la que enseñamos y aprendemos las matemáticas.
En el año 2024, la necesidad de investigar sobre los diferentes enfoques de la enseñanza y aprendizaje de la ciencia de datos se reflejó en la creación de un nuevo grupo temático, Enseñanza y aprendizaje de la ciencia de datos, en el 15th International Congress on Mathematical Education (ICME15). En dicho grupo temático se planteaban como interrogante de discusión: ¿cuáles son los retos que plantea la integración de la ciencia de datos en los planes de estudio escolares o el diseño de un plan de estudios de ciencia de datos a nivel escolar? Además, se establecía como área de interés el estudio de los enfoques curriculares para aplicar la enseñanza y el aprendizaje de la ciencia de datos a nivel escolar.
Dado el creciente interés en el estudio de los enfoques curriculares para integrar la ciencia de datos en el currículum escolar, en este artículo se presenta una investigación sobre el papel que adquiere el sentido estocástico en la educación en datos en el contexto español. Se fijan como interrogantes de investigación:
• ¿qué organizaciones fenomenológicas (grandes ideas, alfabetización y ciclos de investigación) del sentido estocástico se presentan en los diferentes niveles educativos del currículum español?
• ¿qué grandes ideas que vertebran la ciencia de datos, prescrita en el currículum español, son constitutivas a la vez de las materias del conocimiento matemático, de las ciencias de la computación y del conocimiento sustantivo?
Dicha investigación se concreta en el análisis del contenido descriptivo e interpretativo de los Reales Decretos 157/2022, 217/2022 y 243/2022 por los que se establece respectivamente la ordenación y enseñanzas mínimas de la Educación Primaria, Secundaria Obligatoria y del Bachillerato en España.
2. MARCO TEÓRICO: EL PAPEL DEL SENTIDO ESTOCÁSTICO EN LA CIENCIA DE DATOS
Para caracterizar la noción de sentido estocástico se usa el modelo de Fernández y García-García (2024) que lo describe como la unión de la alfabetización, el razonamiento y el pensamiento. Las diferentes caracterizaciones que encontramos en la literatura sobre el significado de alfabetización matemática, estadística, estocástica y, probabilística hacen necesario referirse a cada una de ellas de forma independiente para fundamentar las nociones de sentido estadístico, estocástico y probabilístico. La revisión de la literatura permite identificar diferencias en las nociones de sentido estadístico, estocástico y probabilístico en función del papel que adquiere el razonamiento, los saberes puestos en juegos y la capacidad de predicción. Si bien, en un inicio, se podría considerar englobar los tres en el sentido estocástico, estas diferencias hacen necesario referirse a cada uno de ellos de forma independiente con el fin de integrar la triada matemáticas/estadística/probabilidad que apoye con éxito el desarrollo de la ciencia de datos.
Así pues, ante la dificultad de la caracterización de dichas nociones, se toma en consideración la sugerencia de Weiland y Engledowl (2022) que indica que el análisis del currículum debe empezar por el establecimiento de las grandes ideas clave que serán cruciales para la educación en ciencia de datos y la alfabetización en datos en las etapas de la educación no universitaria. En las siguientes secciones se caracterizan estas visiones organizativas a partir de cuáles son las grandes ideas que describen y conceptualizan las nociones de alfabetización y el sentido.
2.1. Grandes ideas estadísticas, la alfabetización estadística y el sentido estadístico
Gal (2002) presenta un modelo comprensivo de la alfabetización estadística en dos bloques: los elementos relacionados con el conocimiento (habilidades de alfabetización, conocimiento estadístico, conocimiento matemático, conocimiento contextual y cuestiones críticas) y los elementos disposicionales (creencias, actitudes y posicionamiento crítico).
En el contexto iberoamericano, Batanero (2013) traduce el concepto de alfabetización estadística como cultura estadística e indica que incluye dos competencias relacionadas:
(a) Capacidad para interpretar y evaluar críticamente la información estadística, los argumentos apoyados en datos a los fenómenos que las personas pueden encontrar en diversos contextos, incluyendo los medios de comunicación, pero no limitándose a ellos y b) capacidad para discutir o comunicar sus opiniones respecto a tales informaciones estadísticas cuando sea relevante (Batanero 2013, p. 2)
En este mismo documento se define el sentido estadístico como:
(a) La comprensión de las ideas estadísticas fundamentales, que han contribuido al desarrollo de la estadística, se requieren en la resolución de problemas estadísticos y pueden ser enseñadas en varios niveles educativos; (b) la competencia de análisis de datos; (c) el razonamiento a partir de los datos, para realizar inferencias de muestras a poblaciones y/tomar decisiones acertadas en situaciones inciertas (Batanero 2013, p. 1)
Burrill y Biehler (2011) proponen las siguientes ideas estadísticas fundamentales: los datos, la variación, la distribución, la representación, la asociación y la modelización entre dos variables, los modelos probabilísticos para la generación de procesos, el muestreo y la inferencia. Para Batanero (2013) la comprensión de las ideas anteriores y su uso en la resolución de problemas requiere de una competencia mínima de análisis de datos y del desarrollo del razonamiento estadístico. Esta autora indica que uno de los modelos para describir dicho razonamiento es el presentado por Wild y Pfannkuch (1999). Estos autores conciben el razonamiento estadístico como la suma de cuatro dimensiones: reconocer la necesidad de datos, la transnumeración, la percepción de la variación, el razonamiento con modelos estadísticos, la integración de la estadística y el contexto. En la presentación de las ideas estadísticas fundamentales, Batanero (2013) incluye la probabilidad e indica que la característica principal de la estadística es hacer uso de modelos aleatorios. Asimismo, afirma que a nivel escolar son relevantes tres aproximaciones: la concepción clásica, el enfoque frecuencial y la concepción subjetiva. En el trabajo reciente de Batanero y Álvarez-Arroyo (2024) sobre la enseñanza y aprendizaje de la probabilidad, estas autoras clarifican que la probabilidad es parte de la estadística y que está incluida en las matemáticas a nivel escolar. La estadística, en este caso, incluye el análisis exploratorio de datos, la inferencia y la probabilidad, proveyendo de modelos matemáticos que permitan realizar las transiciones del análisis exploratorio de datos a las posibles inferencias.
2.2. Grandes ideas probabilísticas, la alfabetización probabilística y el sentido probabilístico
Heitele (1975) presenta un conjunto de ideas fundamentales para la enseñanza de la probabilidad como son la regla de la adición y producto de probabilidades, la independencia y la composición/probabilidad condicional, la equidistribución y la simetría, la combinatoria, la simulación, la variable estocástica, la ley de los grandes números y el muestreo. La principal diferencia entre los marcos teóricos para la enseñanza de la estadística y la estocástica es que no se presentan los procesos de pensamiento, sino que se describen exclusivamente los conceptos puestos en juego (Burril y Biehler, 2011). Además, indican que su importancia radica en ser la rama de las matemáticas que modeliza relaciones no deterministas, fenómenos aleatorios y decisiones bajo incertidumbre.
Gal (2005) expande su visión de alfabetización estadística a la probabilidad. En su modelo, incluye la capacidad de interpretar y evaluar críticamente información probabilística y fenómenos aleatorios, y se centra en la importancia del contexto, en el que se incluye dicha información. Para Borovcnik (2016), “lo esencial para dicha alfabetización probabilística son las habilidades para comprender el significado y el lenguaje básico de los conceptos probabilísticos y el uso de los argumentos probabilísticos de forma adecuada en las discusiones privadas y públicas” (p. 1496).
Fernández y García-García (2024) presentan un primer acercamiento a la definición de sentido probabilístico como “la unión de la alfabetización, razonamiento y pensamiento probabilístico, donde sugerimos los significados de la probabilidad e ideas estocásticas fundamentales como componentes esenciales” (p. 113).
2.3. El sentido estocástico
Teniendo en cuenta las grandes ideas estadísticas, los principios y componentes de la alfabetización estadística y probabilística, y las características definitorias del sentido estadístico, la CEMat (2021) argumentaba como las grandes ideas matemáticas -modelo, distribución, inferencia, estimación e incertidumbre, introducidas por Cleveland (2001), deben estar organizadas en torno al concepto de sentido estocástico. El CEMat (2021) definía el sentido estocástico como:
la capacidad para hacer frente a una amplia gama de situaciones cotidianas que implican el razonamiento y la interpretación de datos, la elaboración de conjeturas y la toma de decisiones a partir de la información estadística, su valoración crítica y la comprensión y comunicación de fenómenos aleatorios, y la capacidad de realizar algunas predicciones (p. 35).
Esta noción compacta de sentido estocástico integra las nociones de razonamiento estadístico y las diferentes definiciones y niveles de competencia de la alfabetización estadística (Rodríguez-Muñiz et al., 2021) al considerar que la alfabetización matemática combina los grandes principios metodológicos del razonamiento, la resolución de problemas y el pensamiento computacional (CEMat, 2021).
Bajo esta perspectiva, permite a Ruiz-Hidalgo y Flores (2022) describir las componentes que deben organizar el sentido estocástico a nivel curricular: identificación de la aleatoriedad, estudio de datos, comprensión y aplicación de los conceptos básicos de la probabilidad, percepción de la variabilidad y razonamiento con modelos estadísticos y desarrollo y evaluación de inferencias y predicciones. En esta descripción de las componentes que organizan el sentido estocástico, adquieren gran importancia las ideas relacionadas con la probabilidad, que se entiende como el cálculo de la medida de la incertidumbre y la distribución como gran idea que surge al modelar fenómenos estocásticos mediante las distribuciones de probabilidad (CEMat, 2021). En esta propuesta metodológica, el término estocástico se utiliza para destacar la dependencia mutua entre el conocimiento y el razonamiento estadístico y probabilístico, que están estrechamente interconectados y que deben enseñarse juntos (Batanero, 2019).
2.4. De la estadística a la ciencia de datos
Para Breiman (2001), la estadística empieza con los datos y existen dos objetivos para su análisis: (1) la predicción -ser capaces de predecir cuáles van a ser las respuestas a futuras variables de entrada-, y (2) la información -para extraer información sobre cómo la naturaleza asocia las variables de respuesta a las variables de entrada-. Asimismo, afirma la existencia de dos modelizaciones estadísticas para llegar a conclusiones a partir de los datos: la cultura de la modelización de datos y la cultura de la modelización algorítmica. Posteriormente, Donoho (2017) interpreta estas dos culturas estableciendo dos objetivos para el análisis de datos: (1) la inferencia -inferir cómo la naturaleza asocia las variables de respuesta a las variables de entrada- y, (2) la predicción -poder predecir cuáles van a ser las respuestas a futuras variables de entrada.
Gafny y Ben-Zvi (2024) retoman las ideas de Breiman (2001) para la exploración de los modelos basados en datos y la modelización como actividades educativas que están en la intersección de la enseñanza de la estadística clásica y el ámbito de la enseñanza de la ciencia de datos. Invitan en su artículo a reimaginar la educación en datos creando puentes entre la estadística clásica y la ciencia de datos. Estos puentes deben permitir la evolución: (a) desde el uso de pequeños conjuntos de datos a la consideración de las tres dimensiones del big data, volumen, variedad y velocidad; (b) desde la descripción de los datos al uso de modelos basados en datos y la modelización; (c) del reconocimiento de la incertidumbre estadística y contextual a la consideración de la incertidumbre aleatoria, que se refiere al concepto de aleatoriedad y la incertidumbre epistémica, que surge de una falta de conocimiento estadístico o la comprensión del fenómeno; (d) del uso de modelos estadísticos informales al desarrollo de modelos predictivos informales de big data. Así pues, Gafny y Ben-Zvi (2024) identifican como grandes ideas de la ciencia de datos: el big data, la modelización y la incertidumbre.
Para Gould (2024), el papel de la modelización generativa de carácter inferencial a nivel escolar está supeditada a los procesos de modelización que surgen al aplicar los llamados ciclos de datos. Este autor nombra dos propuestas: (a) la propuesta de Wild y Pfannkuch (1999), consistente en las fases de problema, plan, datos, análisis y conclusiones; y (b) en la propuesta de Franklin et al. (2007), que consiste en proponer una pregunta, considerar o recolectar datos, analizar los datos e interpretar los resultados.
En cambio, los modelos predictivos difieren de los modelos tradicionales, ya que no siempre se comunican usando una notación matemática, sino que pueden ser algorítmicos o consistir en conjuntos de algoritmos. Estos conjuntos son complejos y poco transparentes; puede ser difícil explicar con precisión qué factores han influido en los resultados de los modelos (Gould, 2024).
Con la finalidad de que se integre la ciencia de datos a nivel escolar, Lee et al. (2022) proponen un marco para la investigación en datos basado en los procesos de investigación estadística, el campo de la ciencia de datos y las prácticas de un científico de datos. Este marco teórico consiste en un ciclo de seis fases: enmarcar el problema, considerar y recolectar datos, procesar datos, explorar y visualizar los datos, considerar modelos y comunicar y proponer acciones.
Bajo estos principios y, especialmente, teniendo en cuenta el peligro de la desinformación en la era del big data, cada vez es más importante un manejo generalizado y competente de los datos, lo que se conoce como alfabetización en datos (Carmi et al., 2020). Es decir, la alfabetización en datos se define como la capacidad de recopilar, gestionar, evaluar y aplicar datos con una reflexión crítica continua sobre estos procesos (Ridsdale et al., 2015) con un énfasis especial en los procesos de recolección de datos (Witte et al., 2025). Estos autores sugieren una aproximación metodológica interdisciplinar para integrar estas capacidades en el currículum (Witte et al., 2025).
3. METODOLOGÍA
Se ha seleccionado como metodología cualitativa de investigación el análisis de contenido por rigurosidad al permitir examinar los elementos latentes del texto. Esta es una técnica de investigación para codificar haciendo inferencias replicables y válidas de los textos al contexto de uso (Krippendorff, 2018). El contexto de estudio se ha contextualizado en las propuestas educativas en ciencia de dato en Educación Primaria (6-11 años), Secundaria Obligatoria (12-15 años) y Bachillerato (16-17 años) en España. El análisis de contenido se ha realizado en tres fases. En una primera fase y, de forma independiente, los autores del artículo han codificado todas las unidades de información de los Reales Decretos 157/2022, 217/2022 y 243/2022, por los que se establecen respectivamente las enseñanzas mínimas de la Educación Primaria, de la Educación Secundaria Obligatoria y del Bachillerato. Se han codificado en ATLAS.ti (2025) los códigos obtenidos correspondientes a los saberes básicos de la Tabla 1.
En una segunda fase, los diferentes códigos se han agrupado en las categorías descritas en el marco teórico. Dicha categorización se basa en: (a) el estudio de los elementos constitutivos, que se organizan conceptualmente en conocimientos de matemáticas y estadística, en ciencias de la computación y los sustantivos, (b) el análisis de las grandes ideas organizadas conceptualmente para el campo estadístico, probabilístico, estocástico y la ciencia de datos, (c) la alfabetización estadística, probabilística, estocástica y en datos y (d) los ciclos de investigación de cuatro, cinco y seis fases.
Tabla 1
Sistema de categorías para el análisis del papel del sentido estocástico en la ciencia de datos
|
Organización fenomenológica |
Organización conceptual |
|
|
Conocimientos |
Saberes básicos |
|
|
Elementos constitutivos |
Matemáticas y estadística |
Estadística descriptiva, estadística diferencial, probabilidad, algebra lineal, análisis, visualización de datos, modelización predictiva |
|
Sustantivos |
Ciencias, humanidades y ciencias sociales, económicas y finanzas, medicina y ciencias de la salud, lenguas, tecnología, administración |
|
|
Ciencias de la computación |
Programación, algoritmos, bases de datos, procesamiento de datos, manejo de datos, machine learning, ingeniería de datos, big data |
|
|
Grandes ideas |
Estadística |
Gráficos, variación, distribución, asociación, probabilidad, muestreo, inferencia |
|
Probabilística |
Regla de la adición y producto de la probabilidad, independencia, composición, probabilidad condicionada, equidistribución, simetría, combinatoria, simulación, variable estocástica, ley de los grandes números, muestreo |
|
|
Estocástica |
Modelo, distribución, inferencia, estimación, incertidumbre, variabilidad |
|
|
Ciencia de datos |
Big data, incertidumbre epistémica y aleatoria, modelos estadísticos informales y predictivos |
|
|
Alfabetización |
Estadística |
Resolución de problemas, análisis de datos, razonamiento |
|
Probabilística |
Interpretar, evaluar información y fenómenos aleatorios |
|
|
Estocástica |
Razonamiento, interpretación de datos, elaboración de conjeturas, toma de decisiones, valoración crítica, comunicación de fenómenos aleatorios, capacidad de realizar predicciones, emitir juicios |
|
|
En datos |
Recopilación, almacenamiento, análisis e interpretación, representación, alteración, modelización predictiva, machine learning, pensamiento computacional |
|
|
Ciclos de investigación |
Cuatro fases |
Plantear una pregunta, considerar o recolectar datos, analizarlos, interpretar los resultados |
|
Cinco fases |
Problema, plan, datos, análisis, conclusiones |
|
|
Seis fases |
Problema, considerar y recolectar datos, procesar, explorar y visualizar, considerar modelos, y comunicar y proponer acciones |
|
En una tercera fase, dicho sistema de categorías ha sido validado por expertos que han valorado la adecuación entre las diferentes categorías establecidas y los saberes incluidos en el mismo.
Todo ello ha permitido realizar dos tipos de análisis. Un análisis de contenido descriptivo a partir del estudio de la distribución de los códigos en cada uno de los tres Reales Decretos y resumido en las tablas de frecuencias que relacionan los códigos con los documentos, y un análisis de contenido latente a partir del análisis de las tablas de frecuencias de la concurrencia de dos códigos en una misma unidad de información.
Este análisis del contenido descriptivo ha permitido, en primer lugar, determinar las materias constitutivas de los conocimientos matemáticos, de las ciencias de la computación y sustantivos para una propuesta de educación en ciencia de datos. En segundo lugar, ha posibilitado establecer qué organizaciones fenomenológicas del sentido estocástico se presentan en los diferentes niveles educativos. Finalmente, el análisis del contenido latente, a partir del análisis de la concurrencia de las unidades de codificación de los saberes básicos, ha proporcionado información sobre la visión interdisciplinar de la ciencia de datos y cuáles son los conocimientos vertebradores prescritos simultáneamente en las materias del conocimiento matemático, de las ciencias de la computación y del conocimiento sustantivo.
4. ORGANIZACIÓN DEL SENTIDO ESTOCÁSTICO EN LAS MATERIAS DE MATEMÁTICAS
4.1. Organizaciones fenomenológicas del sentido estocástico
Con el fin de dar respuesta a la pregunta de investigación sobre qué organizaciones fenomenológicas del sentido estocástico se presentan en los diferentes niveles educativos del currículum español para las materias de matemáticas, se analizan las definiciones del sentido estocástico para las etapas de Educación Primaria, Secundaria Obligatoria y Bachillerato.
En la etapa de Educación Primaria el sentido estocástico se orienta hacia:
El razonamiento y la interpretación de datos y la valoración crítica, así como la toma de decisiones a partir de información estadística. También comprende los saberes vinculados con la comprensión y la comunicación de fenómenos aleatorios en situaciones de la vida cotidiana (Real Decreto 157/2022, p. 93).
En la etapa de Educación Secundaria Obligatoria comprende:
El análisis y la interpretación de datos, la elaboración de conjeturas, la toma de decisiones a partir de la información estadística, su valoración crítica y la comprensión y comunicación de fenómenos aleatorios en una amplia variedad de situaciones cotidianas (Real Decreto, 217/2022, p. 142).
El Real Decreto 243/2022 por el que se establecen la ordenación y las enseñanzas mínimas del Bachillerato, describe en su página 260 la misma definición del sentido estocástico que para la Educación Secundaria Obligatoria, pero amplía el campo de estudio de las situaciones cotidianas a todo tipo de situaciones.
Dichas definiciones se asemejan a la aportada por la CEMat (2021), ya que proporcionan una organización fenomenológica del contenido a partir de la interpretación de datos, la toma de decisiones, la valoración crítica de la información estadística y la comprensión y comunicación de los fenómenos aleatorios. Además, en el caso de la etapa de Educación Primaria se complementa con el razonamiento, entendiéndose que es el estadístico, pero sin nombrarlo. Sin embargo, respecto a la definición de la CEMat (2021) no se consideran capacidades como la elaboración de conjeturas o la capacidad de realizar predicciones. Mientras que la visión de la CEMat (2021) es otorgarle al sentido estocástico una aproximación cultural de la modelización generativa e inferencial y predictiva de los saberes puestos (Breiman, 2001; Donoho, 2017), las propuestas de los Reales Decretos que organizan las enseñanzas de la matemática solo presentan una visión cultural de la modelización generativa.
4.2. Organizaciones que enlazan los conocimientos del sentido matemático
En esta sección se presenta el análisis del contenido descriptivo y frecuencial de la aparición de las grandes ideas legisladas y de las capacidades puestas en juego. Tal y como se observa en la Tabla 2, la frecuencia de aparición de las ideas estadísticas (gráficas, variación, distribución, asociación, probabilidad, muestreo e inferencia), probabilísticas (independencia, probabilidad, probabilidad condicionada, equiprobabilidad, técnicas de recuento, variable aleatoria, ley de los grandes números y muestreo) y estocásticas (modelo, distribución, inferencia, estimación, incertidumbre y variabilidad) es creciente en los textos legislativos de las tres etapas.
Tabla 2
Análisis frecuencial de la aparición de las grandes ideas estadísticas, estocásticas y probabilísticas en los Reales Decretos 157/2022, 217/2022 y 243/2022 que establecen la ordenación y las enseñanzas mínimas de la Educación Primaria, Secundaria Obligatoria y Bachillerato
|
Ideas |
Educación Primaria |
Educación Secundaria Obligatoria |
Bachillerato |
|
Estadísticas |
20 |
38 |
43 |
|
Estocásticas |
23 |
48 |
58 |
|
Probabilísticas |
17 |
18 |
35 |
En los tres documentos se describe el sentido estocástico a partir de tres grandes organizadores de los saberes básicos: la organización y análisis de datos, la incertidumbre y la inferencia. Sin embargo, se observa que al describir los saberes básicos de cada uno de los tres organizadores en los tres documentos tienen una mayor presencia las ideas correspondientes al sentido estocástico.
Ahondando en las capacidades puestas en juego y descritas en los organizadores fenomenológicos de la alfabetización estadística (resolución de problemas, análisis de datos y razonamiento), probabilística (interpretar, evaluar información y fenómenos aleatorios) y estocástica (razonamiento, interpretación de datos, elaboración de conjeturas, toma de decisiones, valoración crítica, comunicación de fenómenos aleatorios, realizar predicciones, emitir juicios) se ha procedido al estudio frecuencial de la aparición de dichas categorías, que se resume en la Tabla 3.
El estudio frecuencial permite interpretar que, a lo largo de las tres etapas, se insta a un mayor desarrollo de las capacidades. Mientras que en las etapas de Educación Primaria y Secundaria Obligatoria tienen predominio el desarrollo de las capacidades correspondientes a la alfabetización estadística, en Bachillerato adquieren más importancia las capacidades correspondientes a la alfabetización estocástica. En resumen, a nivel de organización fenomenológica, las materias de Educación Primaria, Secundaria Obligatoria y Bachillerato se orientan a la interpretación de los datos, la toma de decisiones y la valoración crítica de la información estadística y la comprensión y comunicación de los fenómenos aleatorios. Las grandes ideas de organización y análisis de datos, el modelo, la distribución, la inferencia y la incertidumbre son las organizadoras del contenido matemático descritas en la literatura como las grandes ideas del sentido estocástico. Sin embargo, a nivel de capacidades, se insta al desarrollo de la alfabetización estadística poniendo el énfasis en la resolución de problemas y el análisis de datos. Este énfasis en la resolución de problemas como gran cambio metodológico para avanzar hacia una educación en la ciencia de datos, como también establece Rodríguez-Muñiz (2023).
Tabla 3
Análisis frecuencial de la aparición de las capacidades definitorias de la alfabetización estadística, probabilística y estocástica en los Reales Decretos 157/2022, 217/2022 y 243/2022 que establecen la ordenación y las enseñanzas mínimas de la Educación Primaria, Secundaria Obligatoria y Bachillerato
|
Alfabetización |
Educación Primaria |
Educación Secundaria Obligatoria |
Bachillerato |
|
Estadística |
40 |
85 |
59 |
|
Estocástica |
36 |
68 |
62 |
|
Probabilísticas |
24 |
31 |
40 |
5. LA VISIÓN INTERDISCIPLINAR DE LA CIENCIA DE DATOS EN EL CURRÍCULUM ESPAÑOL
Para poder analizar, tal y como indicaba Conway (2010) que la ciencia de datos se encuentra en la intersección de tres elementos constitutivos, las matemáticas y la estadística, los conocimientos sustantivos de los campos donde surgen los problemas y el conjunto de datos a analizar, y la computación, se han analizado los saberes básicos descritos en las diferentes materias del currículo además de las materias de matemáticas. La Figura 1 resume las materias constitutivas de la ciencia de datos que incluyen en la descripción de los saberes básicos las ideas organizadoras del sentido estadístico, estocástico y probabilístico.
Las orientaciones de las diferentes materias proponen una organización curricular interdisciplinar frente a un trabajo exclusivamente disciplinar. Por ejemplo, en la materia de geografía e historia de Educación Secundaria Obligatoria se insta el uso de los procedimientos que aportan diferentes áreas de conocimiento, e indica “facilita el planteamiento de estrategias interdisciplinares a lo largo de los cuatro cursos de la etapa [de secundaria obligatoria de 13 a 16 años]” (Real Decreto 217/2022, p. 41676). Aunque en los diferentes textos en ningún momento se nombra la transdisciplinariedad organizativa del currículo, esta surge de la necesidad de la integración del currículum con el entorno y declara la necesidad de “crear escenarios diversos en los que desarrollar iniciativas y proyectos en situaciones reales que propicien la participación y el compromiso con el entorno y la comunidad” (Real Decreto 217/2022, p. 41676). Así pues, las matemáticas son, en su naturaleza instrumental, la “herramienta fundamental para áreas de conocimientos científico, social, tecnológico y artístico” (Real Decreto 243/2022, p. 260).
Figura 1
Materias constitutivas de la ciencia de datos por nivel educativo
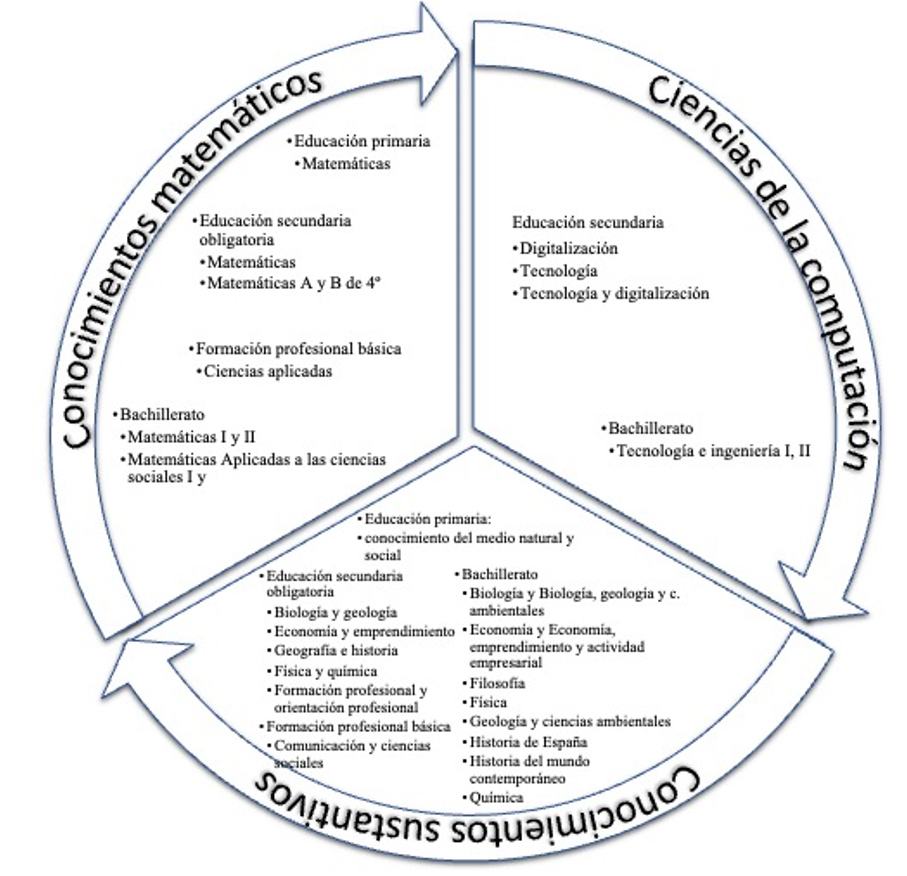
Esta orientación metodológica interdisciplinar concuerda con la propuesta de Cukic et al. (2020) y Witte et al. (2025). Ya que estos autores argumentan sobre la necesidad de incorporar la ciencia de datos de forma que permita integrar los conocimientos y las competencias necesarias para una adecuada investigación estadística. Debe mencionarse que en la descripción de los saberes básicos de las materias de las ciencias de la computación y los conocimientos sustantivos no se nombra la probabilidad. Permitiendo, tal y como se dictamina en los textos legislativos, que los conocimientos sustantivos de las diferentes materias proporcionen al futuro científico de datos una comprensión del contexto disciplinar de la estadística a la par que una visión interdisciplinar de las materias organizadas. A su vez, la integración de las materias de matemáticas y de las ciencias de la computación debe permitir el desarrollo de las competencias, en general, y la de digitalización, en particular. En los textos legislativos de las tres etapas se describe la competencia digital de la misma forma, indicando que:
[…] incluye la alfabetización en información y datos, la comunicación y la colaboración, la educación mediática, la creación de contenidos digitales (incluida la programación), la seguridad (incluido el bienestar digital y las competencias relacionadas con la ciberseguridad), asuntos relacionados con la ciudadanía digital, la privacidad, la propiedad intelectual, la resolución de problemas y el pensamiento computacional y crítico (Real Decreto 157/2022, p. 22).
Esta indicación se alinea con la definición sobre alfabetización de datos propuesta por Ridsdale et al. (2015) al enfatizar el desarrollo de la resolución de problemas, el pensamiento computacional y crítico.
6. LAS GRANDES IDEAS ESTOCÁSTICAS VERTEBRADORAS DE LA CIENCIA DE DATOS PRESCRITAS EN EL CURRÍCULO ESPAÑOL
El análisis de la concurrencia de las ideas estadísticas, estocásticas y probabilísticas, así como de las materias de los conocimientos matemáticos, de las ciencias de la computación y de los conocimientos sustantivos se presenta en la Figura 2.
Figura 2
Grandes ideas puente entre los elementos constitutivos de la ciencia de datos
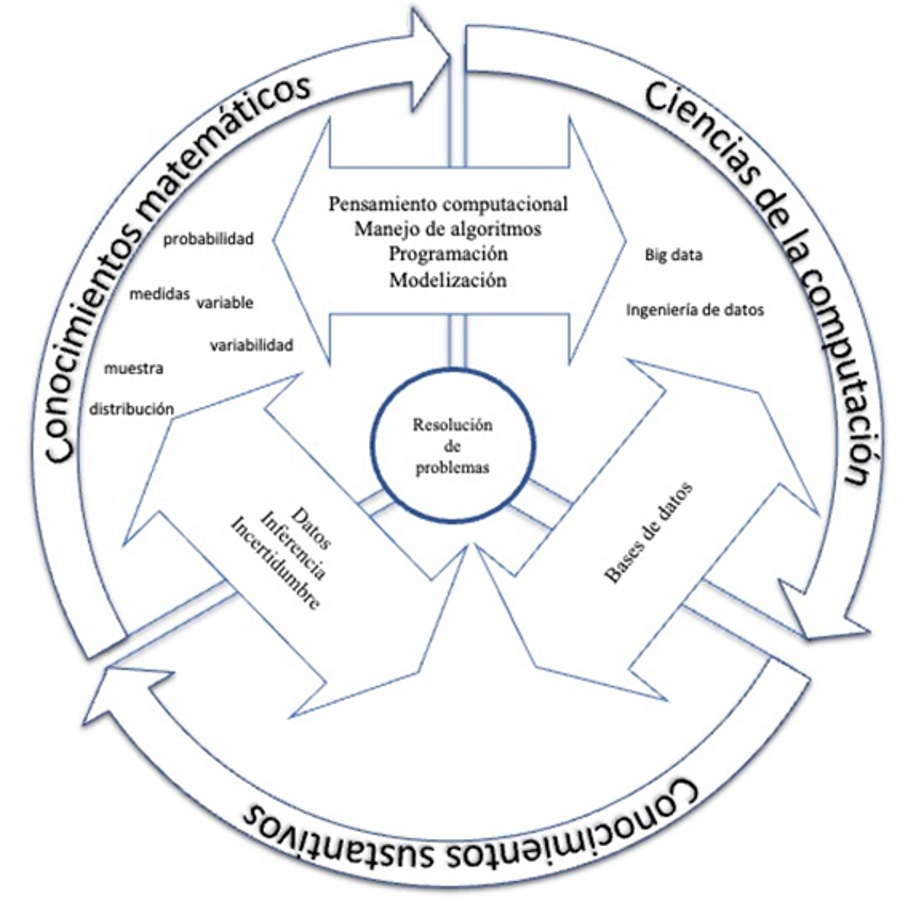
En el centro de la figura se ha situado la resolución de problemas porque, como hemos argumentado en la sección anterior, en los Reales Decretos se insta al desarrollo de la alfabetización en datos poniendo énfasis a la resolución de problemas en las materias matemáticas. En las materias de las ciencias de la computación se describe “el desarrollo de aplicaciones informáticas que resuelvan un problema concreto” (Real Decreto 217/2022, p. 169). En la materia de biología y geología de Educación Secundaria se orienta a “resolver problemas” (Real Decreto 217/2022, p. 38). Lo anterior concuerda con lo señalado por de Rodríguez-Muñiz (2023) sobre la necesidad de enfatizar la resolución de problemas como uno de los cambios metodológicos necesarios en el currículo para avanzar hacia la educación en ciencia de datos. Además, coincide con uno de los grandes principios metodológicos propuestos para la CEMat (2021) para dotar de sentido al currículo.
6.1. La bidireccionalidad entre los conocimientos matemáticos y las ciencias de la computación
El análisis frecuencial de la concurrencia de códigos, saberes básicos, entre las materias correspondientes a los conocimientos matemáticos y de ciencias de la computación han permitido establecer como conocimientos concurrentes: el pensamiento computacional, el manejo de algoritmos, la programación y la modelización. Un ejemplo de esta bidireccionalidad de los conocimientos la encontramos entre las materias de Matemáticas y Tecnología y digitalización de Educación Secundaria Obligatoria. En la materia de Matemáticas se describe como saber asociado a la organización y análisis de datos, la “representación mediante diferentes tecnologías” (Real Decreto 217/2022, p. 149) con el fin de “utilizar los principios del pensamiento computacional organizando datos, descomponiendo en partes, reconociendo patrones, interpretando, modificando y creando algoritmos, para modelizar situaciones y resolver problemas de forma eficaz” (Real Decreto 217/2022, p. 143). En la materia de Tecnología y Digitalización se describe que el pensamiento computacional “implica la puesta en marcha de procesos ordenados que incluyen la descomposición del problema, la secuenciación del proceso y el diseño de algoritmos para implementarlos en un programa informático” (Real Decreto 217/2022, p. 175).
Esta bidireccionalidad entre los conocimientos matemáticos y las ciencias de la computación ahonda en la visión procedimental y práctica de la ciencia de datos que contempla Engel (2017).
6.2. La bidireccionalidad entre los conocimientos matemáticos y los conocimientos sustantivos
Por otra parte, el análisis frecuencial de la concurrencia de códigos entre las materias correspondientes a los conocimientos matemáticos y sustantivos han permitido establecer los siguientes conocimientos coincidentes: el tratamiento de los datos, la inferencia, la incertidumbre y la distribución.
Iniciamos el análisis de la concurrencia a partir del estudio bidireccional de los datos. En los niveles de Educación Primaria y Educación Secundaria Obligatoria se han dictaminado bloques organizadores del sentido estocástico: la organización y análisis de datos. En la etapa de Educación Primaria y 1º, 2º y 3º de Educación Secundaria Obligatoria se establecen como estrategias para la realización de un estudio estadístico sencillo: formulación de preguntas, recogida, registro y organización de datos, representación, visualización y modelización de datos mediante medidas de centralización y dispersión y obtención de conclusiones. Esta propuesta de estudio estadístico está en consonancia con la propuesta por Franklin et al. (2007) para los ciclos de cuatro fases.
En cambio, en las materias de Matemáticas A y B de Educación Secundaria Obligatoria se establecen como estrategias la recogida y organización de datos de situaciones de la vida cotidiana, análisis de interpretación de tablas y gráficos estadísticos, modelización de datos mediante medidas de centralización y dispersión y la regresión lineal junto con el “análisis del alcance de las conclusiones de un estudio estadístico valorando la representatividad de la muestra” (Real Decreto 217/2022, p. 154). La importancia que adquiere la modelización en la asociación de variables mediante la regresión lineal hace valorar la consideración de las diferentes etapas del diseño del estudio estadístico está relacionada con los ciclos de seis fases caracterizadas por Lee et al. (2022), que se indican en la sección 2.4 y se resumen en la Tabla 1.
Por otra parte, en la materia de Biología y Geología de Educación Secundaria Obligatoria se establece como capacidad a desarrollar: “Diseñar la experimentación, la toma de datos y el análisis de fenómenos biológicos o geológicos de modo que permitan responder a preguntas concretas y contrastar una hipótesis planteada” (Real Decreto 217/2020, p. 37).
En relación con el estudio bidireccional del conocimiento de la inferencia, el análisis de la frecuencia de concurrencia entre las materias correspondientes a los conocimientos sustantivos y el código correspondiente al saber básico de la inferencia ha permitido identificar que en la materia de Física y Química de Educación Secundaria Obligatoria se insta al trabajo experimental y los proyectos de investigación, “haciendo inferencias válidas de las observaciones y obteniendo conclusiones” (Real Decreto 217/2022, p. 85). Además, la inferencia se prescribe como una componente organizadora del sentido estocástico en el currículum de Educación Primaria, Secundaria Obligatoria y las materias de Matemáticas aplicadas a las Ciencias Sociales I y II y las Matemáticas Generales de Bachillerato. Se indica que la inferencia consiste en el “diseño de estudios estadísticos relacionados con las ciencias sociales utilizando herramientas digitales. Técnicas de muestreo sencillas” (Real Decreto 243/2022, p. 277), que el trabajo con muestras tiene como fin emitir juicios y tomar decisiones, siendo estas capacidades elementos definitorios del sentido estocástico según la CEMat (2021).
Así pues, se puede concluir que la inferencia, un componente definitorio del sentido estocástico establecidos por Ruiz-Hidalgo y Flores (2022), es un conocimiento bidireccional constituyente del conocimiento matemático y sustantivo.
En tercer lugar, se examina la bidireccionalidad de la incertidumbre reconocida por la CEMat (2021) como una de las grandes ideas del sentido matemático y por Cleveland (2001) como una de las ideas definitorias de la ciencia de datos. En el currículum para la Educación Primaria y Secundaria Obligatoria se señala como uno de los grandes retos del siglo XXI la incertidumbre, estableciendo como desafío: “aceptar la incertidumbre como una oportunidad para articular respuestas más creativas, aprendiendo a manejar la ansiedad que puede llevar pareja” (Real Decreto 157/2022, p. 18). Esta oportunidad se entiende en las materias constitutivas de los conocimientos sustantivos como la exigencia de “una mente compleja, capaz de pensar en términos sistémicos, abiertos y con un alto nivel de incertidumbre” (Real Decreto 157/2022, p. 19). En la materia de Educación Física se indica que este carácter sistémico de la incertidumbre está relacionado con “tomar decisiones, definir metas, elaborar planes sencillos, secuenciar acciones, ejecutar lo planificado, analizar qué ocurre durante el proceso, cambiar de estrategia si fuera preciso y valorar finalmente el resultado” (Real Decreto 157/2022, p. 53). Así pues, consideramos que esta incertidumbre sistémica se prevé que surja en el proceso de aprendizaje, es decir, en el proceso de creación de significados y, por lo tanto, estará relacionada con la incertidumbre epistémica. Sin embargo, no llegaría a conceptualizarse como la incertidumbre epistémica que surge por una falta de conocimiento estadístico o la comprensión del fenómeno, tal y como indican Gafny y Ben-Zvi (2024). Para estos autores, esta falta de reconocimiento de la incertidumbre sistémica dificultaría la conceptualización de la incertidumbre aleatoria y sería un hándicap para poder reimaginar, desde estas materias, las relaciones necesarias para el establecimiento de puentes entre la estadística y la ciencia de datos. Además, la incertidumbre es uno de los organizadores del sentido estocástico en el currículo de las materias de matemáticas. La concurrencia entre la palabra incertidumbre y los conocimientos probabilísticos descritos ha permitido identificar los saberes dictaminados para cada uno de los niveles educativos. En Educación Primaria se relaciona la incertidumbre con situaciones de la vida cotidiana para la “cuantificación y estimación subjetiva y mediante la comprobación de la estabilización de las frecuencias relativas en experimentos aleatorios repetitivos” (Real Decreto 157/2022, p. 107). En la etapa de Educación Secundaria Obligatoria incorpora a la definición anterior la noción de azar y dictamina la distinción entre fenómenos deterministas y aleatorios en experimentos simples y compuestos. En Bachillerato se introducen las nociones de equiprobabilidad, independencia, probabilidad condicionada y los teoremas de probabilidad total y de Bayes. También se señala “el concepto de probabilidad como medida de la incertidumbre” (Real Decreto 217/2022, p. 141), que se relaciona fenomenológicamente con el sentido de la medida al describir “la probabilidad como medida asociada a la incertidumbre de experimentos aleatorios: interpretaciones subjetiva, clásica y frecuentista” (Real Decreto 217/2022, p. 148). Así pues, se prescriben las tres aproximaciones a la probabilidad, concepción clásica, el enfoque frecuencial y la concepción subjetiva, que indica como relevantes Batanero (2013), siendo estos significados de la probabilidad componentes esenciales de la definición de sentido probabilístico descrita por Fernández y García-García (2024).
7. CONCLUSIONES SOBRE EL PAPEL DEL SENTIDO ESTOCÁSTICO EN LA EDUCACIÓN EN CIENCIA DE DATOS
La organización fenomenológica de las materias de matemáticas en el currículum español vigente se realiza a partir de la interpretación de datos, la toma de decisiones, la valoración crítica de la información estadística y la comprensión y comunicación de los fenómenos aleatorios. Además, para la etapa de Educación Primaria se describe la capacidad de razonamiento, pero no se consideran otras capacidades definitorias del sentido estocástico introducidas por la CEMat (2021) como la elaboración de conjeturas o la realización de predicciones. Los saberes básicos se organizan a partir de las siguientes grandes ideas: la organización y análisis de datos, el modelo, la distribución, la inferencia y la incertidumbre. Sin embargo, a nivel de capacidades se insta al desarrollo de la alfabetización estadística poniendo el énfasis en la resolución de problemas y el análisis de datos.
Se concluye que el término estocástico se utiliza, tal y como indica Batanero (2019), para destacar la dependencia mutua entre el conocimiento y el razonamiento estadístico y probabilístico. Asimismo, el uso del término sentido estocástico está en concordancia con la definición presentada por la CEMat (2021), asociada a una visión cultural de la modelización generativa definida previamente por Breiman (2001) y Donoho (2017). Se insta a proveer de modelos matemáticos que favorezcan realizar transiciones entre el análisis exploratorio de datos y las posibles inferencias, que están en consonancia con las propuestas que realizan Batanero y Álvarez-Arroyo (2024).
A nivel metodológico, la organización del fenómeno estocástico desde una perspectiva interdisciplinar es coherente con la propuesta por Witte et al. (2025) para integrar las capacidades necesarias para la alfabetización de datos en el currículum. El objetivo de esta visión interdisciplinar es el desarrollo de competencias, en general, y la competencia digital, en particular. La competencia digital, que incluye la alfabetización de datos se alinea con la propuesta por Ridsdale et al. (2015) al incluir la resolución de problemas, el pensamiento computacional y el pensamiento crítico. Por consiguiente, se pone el foco de atención en la resolución de problemas como eje vertebrador de la actividad matemática a desarrollar en las materias de matemáticas, de las ciencias de la computación y de los conocimientos sustantivos. Para Rodríguez-Muñiz (2023), la resolución de problemas junto con el uso de la tecnología son dos de los cambios metodológicos necesarios para avanzar hacia la educación en la ciencia de datos. A nivel tecnológico, el pensamiento computacional, el manejo de algoritmos, la programación y la modelización son las grandes ideas prescritas en los conocimientos matemáticos y los conocimientos de las ciencias de la computación como saberes básicos que concurren en los documentos legislativos vigentes del currículo español para las tres etapas educativas. Así pues, tal y como indica la CEMat (2021), se dictamina a nivel metodológico la incorporación del pensamiento computacional en el currículo, asociado a su carácter procesual y práctico que adquiere en la ciencia de datos según establecen Engel (2017) y Yan y Davis (2019).
Las grandes ideas del sentido estocástico de los datos, la incertidumbre y la inferencia se prescriben tanto en las materias de matemáticas como en las materias de conocimientos sustantivos. Para la materia de Matemáticas de las etapas de Educación Primaria y Secundaria obligatoria establece como estrategia para su integración la realización de un estudio estadístico. Esta propuesta de estudio estadístico concuerda con la propuesta de cinco fases del ciclo de investigación estadística presentada por Franklin et al. (2007). En cambio, en las materias de Matemáticas A y B de 4º de ESO y Matemáticas I, II y las Matemáticas aplicadas a las Ciencias Sociales I y II de Bachillerato se proponen modelos de seis ciclos al incluir la modelización. En este caso, los procesos de investigación de seis ciclos prescritos se asemejan al modelo propuesto por Lee et al. (2022) para los procesos de investigación en datos. En el caso de Educación Secundaria Obligatoria se propone una modelización inferencial y en Bachillerato una modelización de carácter predictivo. Así pues, se dictaminan a lo largo de las tres etapas, las dos visiones culturales de la modelización introducidas por Breiman (2001). Estos modelos introducidos en las materias de matemáticas proveen de un importante puente conceptual hacia los modelos predictivos usados en la ciencia de datos, donde la incertidumbre puede estar implícita, pero está siempre presente (Gould, 2024).
En el currículum español se propone, como gran reto, la aceptación de la incertidumbre como una oportunidad para articular respuestas más creativas. En las materias sustantivas se aporta una visión de la incertidumbre sistémica relacionada con la comprensión del fenómeno. Pero, no se conceptualiza como la incertidumbre sistémica que surge debido a la falta de conocimiento estadístico, tal y como la definen Gafny y Ben-Zvi (2024). Estos autores invitan a reimaginar la educación en datos creando puentes entre la estadística clásica y la ciencia de datos.
La propuesta curricular española favorece la creación de puentes entre los conocimientos y capacidades definitorios del sentido estocástico y la ciencia de datos. En primer lugar, al favorecer la interdisciplinariedad entre las materias de matemáticas donde se prescribe el trabajo con datos a las materias de las ciencias de la computación donde se incluye como saber básico el big data. En segundo lugar, al proponer el análisis de datos bajo las premisas de la cultura generativa e inferencial de los datos. En tercer lugar, al introducir la cultura de la modelización predictiva que favorecerá la comprensión de modelos predictivos informales del big data y los algoritmos asociados a modelos predictivos formales. Sin embargo, en los textos legislativos del currículum no se describen los principios que permitan crear puentes entre el reconocimiento de la incertidumbre estadística y la incertidumbre epistémica.
En conclusión, aunque la ciencia de datos no está directamente dictaminada en el currículum español vigente como si lo está en países como Estados Unidos, Australia, Canadá o Nueva Zelanda, entre otros, si se establece la alfabetización en datos como un requisito para adquirir las competencias claves que permita al alumnado enfrentarse a los retos del siglo XXI. Además, se insta a una organización interdisciplinar de las materias que deben permitir integrar los tres campos constitutivos de la ciencia de datos, los conocimientos de matemáticas, en ciencias de la computación y los conocimientos sustantivos.
En ellas el sentido estocástico, como organizador fenomenológico del estudio de los datos, tiene un papel predominante al convertirse en una herramienta para la resolución de los problemas basados en datos que surgen en los contextos de las materias de los conocimientos sustantivos y que se automatizan mediante los conocimientos de las materias de la computación.
Agradecimiento: Proyecto 2023-1-CY01-KA220-SCH-000164724
REFERENCIAS BIBLIOGRÁFICAS
ATLAS.ti Scientific Software Development GmbH. (2025). ATLAS.ti Mac (versión 25) [Software de análisis de datos cualitativos]. https://atlasti.com
Batanero, C. (2013). Sentido estadístico: componentes y desarrollo. En J.M. Contreras, G.R. Cañadas, M.M. Gea y P. Arteaga (Eds.), Actas de las Jornadas Virtuales en Didáctica de la Estadística, Probabilidad y Combinatoria (pp. 55-61). Departamento de Didáctica de la Matemática de la Universidad de Granada.
Batanero, C. (2019). Treinta años de investigación en educación estocástica: Reflexiones y desafíos. En J.M. Contreras, M.M. Gea, M.M. López-Martín y E. Molina-Portillo (Eds.), Actas del Tercer Congreso Internacional Virtual de Educación Estadística (pp. 1-15). FQM126.
Batanero, C., y Álvarez-Arroyo, R. (2024). Teaching and learning of probability. ZDM Mathematics Education, 56, 5-17. https://doi.org/10.1007/s11858-023-01511-5
Borovcnik, M. (2016). Probabilistic thinking and probability literacy in the context of risk. Educação Matemática Pesquisa, 18(3), 1491-1516.
Breiman, L. (2001). Statistical modeling: The Two Cultures. Statistical Science, 16(3), 199-231.
Burril, G. (2023). An International look at the Status of Statistics Education. En G.F. Burril, L. de Oliveira Souza y E. Reston (Eds.), Research on Resoning with Data and Statistical Thinking: International Perspectives. Advances in Mathematics Education (pp. 11-16). Springer. https://doi.org/10.1007/978-3-031-29459-4_2
Burrill, G. y Biehler, R. (2011). Fundamental statistical ideas in the school curriculum and in training teachers. En C. Batanero, G. Burrill y C. Reading (Eds.), Teaching statistics in school mathematics. Challenges for teaching and teacher education - A joint ICMI/IASE study (pp. 57-69). Springer. https://doi.org/10.1007/978-94-007-1131-0_10
Carmi, E., Yates, S.J., Lockley, E. y Pawluczuk, A. (2020). Data citizenship: Rethinking data literacy in the age of disinformation, misinformation, and malinformation. Internet Policy Review, 9(2), 1-22. https://doi.org/10.14763/2020.2.1481
CEMat (2021). Bases para la elaboración de un currículo de Matemáticas en Educación no Universitaria. Comité Español de Matemáticas.
Cleveland, W.S. (2001). Data Science: An Action Plan for Expanding the Technical Areas of the Field of Statistics. International Statistical Review, 69(1) 21-26.
Conway, D. (2010). The data science Venn diagram. Databist [Webpage]. http://drewconway.com/zia/2013/3/26/the-data-science-venn-diagram
Cukic, B., Hague, D. y Maher, M.L. (2020). An innovative interdisciplinary undergraduate Data Science Program: Pathways and Experience. En 2020 IEEE Frontiers in Education Conference (FIE) (pp. 1-5). https://doi.org/10.1109/FIE44824.2020.9273976
Donoho, D. (2017). 50 years of Data Science. Journal of Computational and Graphical Statistics, 26(4), 745-766. https://doi.org/10.1080/10618600.2017.1384734
Drozda, Z., Johnstone, D. y Van Horne, B. (2022). Previewing the national landscape of K-12 data science implementation. En Workshop on Foundations of Data Science for Students in Grades K-12. Valhalla Foundation.
Engel, J. (2017). Statistical Literacy for Active Citizenship: A call for Data Science Education. Statistics Education Research Journal, 16(1), 44-49. https://doi.org/10.52041/serj.v16i1.213
Fernández, N. A., y García-García, J. I. (2024). Sentido probabilístico: un primer acercamiento. En M. Sánchez, M.S. García y A. Castañeda (Eds.), Perspectivas actuales de la Educación Matemática (pp. 107-116). Editorial SOMIDEM. https://doi.org/10.24844/SOMIDEM/S3/2024/01-10
Finzer, W. (2013). The Data Science Education Dilemma. Technology Innovations in Statistics Education, 7(2), 1-9. https://doi.org/10.5070/T572013891
Franklin, C., Kader, G., Mewborn, D., Moreno, J., Peck, R.M. y Scheaffer, R. (2007). Guidelines for assessment and instruction in statistics education (GAISE) Report: A Pre-K-12 curriculum framework. American Statistical Association.
Gafny, R. y Ben-Zvi, D. (2024). Reimagining data education: Bridging between classical statistics and data science. En S. Podworny, D. Frischemeier, M. Dvir y D. Ben-Zvi (Eds.), Minerva School 2022: Reasoning with data models and modeling in the big data era (pp. 69-80). https://doi.org/10.17619/UNIPB/1-1815
Gal, I. (2002). Adult’s statistical literacy: Meaning, components, responsibilities. International Statistical Review, 70(1), 1-25.
Gal, I. (2005). Towards “Probability Literacy” for all Citizens: Building Blocks and Instructional Dilemmas. En G.A. Jones (Ed.), Exploring Probability in School. Mathematics Education Library (vol. 40, pp. 39-63). Springer. https://doi.org/10.1007/0-387-24530-8_3
Gould, R. (2024). Traditional statistical models in a sea of data: teaching introductory data science. En S. Podworny, D. Frischemeier, M. Dvir y D. Ben-Zvi (Eds.), Minerva School 2022: Reasoning with data models and modeling in the big data era (pp. 81-90). https://doi.org/10.17619/UNIPB/1-1815
Heitele, D. (1975). An epistemological view on fundamental stochastic ideas. Educational Studies in Mathematics, 6(2), 187-205.
IDSSP Curriculum Team. (2019). Curriculum frameworks for introductory data science. IDSS.
Krippendorff, K. (2018). Content analysis: An introduction to its methodology (4th ed.). Sage Publications. https://doi.org/10.4135/9781071878781
Lee, H. S., Mojica, G.M., Thrasher, E.P. y Baumgartner, P. (2022). Investigating data like a data scientist: Key practices and processes. Statistics Education Research Journal, 21(2), 3. https://doi.org/10.52041/serj.v21i2.41
Real Decreto 157/2022, de 1 de marzo, por el que se establecen la ordenación y las enseñanzas mínimas de la Educación Primaria. Boletín Oficial del Estado, 52, de 2 de marzo de 2022.
Real Decreto 217/2022, de 29 de marzo, por el que se establece la ordenación y las enseñanzas mínimas de la Educación Secundaria Obligatoria. Boletín Oficial del Estado, 76, de 30 de marzo de 2022.
Real Decreto 243/2022, de 5 de abril, por el que se establecen la ordenación y las enseñanzas mínimas del Bachillerato. Boletín Oficial del Estado, 82, de 6 de abril de 2022.
Ridsdale, C., Rothwell, J., Smit, M., Ali-Hassan, H., Bliemel, M., Irvine, D., Kelley, D., Matwin, S. y Wuetherick, B. (2015). Strategies and best practices for data literacy education: Knowledge Synthesis Report. Dalhousie University. https://doi.org/10.13140/RG.2.1.1922.5044
Rodríguez-Muñiz, L.J. (2023). Educar en matemáticas en la era de los datos. Encuentros multidisciplinares, 25(74), 1-9.
Rodríguez-Muñiz, L.J., Muñiz-Rodríguez, L. y Aguilar, Á. (2021). El recuento y las representaciones manipulativas. Los primeros pasos de la alfabetización estadística. PNA, 15(4), 311-338.
Ruiz-Hidalgo, J.F., y Flores, P. (2022). Sentido matemático escolar. En L. Blanco, N. Climent, M.T. González, A. Moreno, G. Sánchez-Matamoros, C. de Castro y C. Jiménez (Eds.), Aportaciones al desarrollo del currículo desde la investigación en educación matemática (pp. 56-79). Universidad de Granada.
Tukey, J.W. (1962). The future of data analysis. The Annals of Mathematical Statistics, 3(1), 1-67.
Weiland, T. y Engledowl, C. (2022). Transforming Curriculum and Building Capacity in K-12 Data Science Education. Harvard Data Science Review, 4(4), 1-20. https://doi.org/10.1162/99608f92.7fea779a
Wild, C.J. y Pfannkuch, M. (1999). Statistical Thinking and Empirical Enquiry. International Statistical Review, 67(3), 223-265.
Witte, V., Schwering, A. y Frischemeier, D. (2025). Strengthening Data Literacy in K-12 Education: A Scoping Review. Education Sciences, 15(1), 25. https://doi.org/10.3390/educsci15010025
Yan, D. y Davis, G. E. (2019). A First Course in Data Science. Journal of Statistics Education, 27(2), 99-109. https://doi.org/10.1080/10691898.2019.1623136
Como citar:
Serradó, A. y Lucia, M. (2025). El papel del sentido estocástico en la educación en la ciencia de datos. Revista de Educación Estadística, 4, 1-25. https://doi.org/10.29035/redes.4.1.3

Esta obra está bajo una licencia de Creative Commons
Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional.
-
1 *Autor de correspondencia: anaserradobayes@lasallebuenconsejo.es (A. Serradó)
https://orcid.org/0000-0002-7701-8271 (anaserradobayes@lasallebuenconsejo.es).
2 https://orcid.org/0009-0005-2258-6924 (marialuciavargas@lasallebuenconsejo.es).
