Revista de Educación Estadística https://revistaeduest.ucm.cl/ Vol. 4, pp. 1-32, ene. 2025 - dic. 2025 ISSN 2810-6164

DOI: https://doi.org/10.29035/redes.4.1.6

 

EXPLORANDO EL DESARROLLO PROFESIONAL SOBRE EDUCACIÓN ESTADÍSTICA DEL PROFESORADO EN ACTIVO

Explorando o desenvolvimento profissional dos professores em serviço no ensino de estatística

Exploring in-service teachers’ professional development in statistical education

Ángel Alsina1

Universitat de Girona (Girona, España)

Claudia Vásquez2

Pontificia Universidad Católica de Chile (Villarrica, Chile)

Luis José Rodríguez-Muñiz3

Universidad de Oviedo (Oviedo, España)

Ernesto Sánchez4

Centro de Investigación y de Estudios Avanzados del Instituto Politécnico Nacional (Ciudad de México, México)

 

Resumen

El objetivo de este artículo es explorar la autovaloración sobre la preparación y los conocimientos centrales para enseñar estadística del profesorado en activo de las etapas de educación infantil, primaria y secundaria, como punto de partida para el diseño de planes de desarrollo profesional del profesorado en educación estadística. Como preámbulo se revisan algunos marcos que conceptualizan la actividad profesional del profesorado en estadística y las ideas centrales de la estadística para su enseñanza. Los datos se obtuvieron administrando un cuestionario online sobre enseñanza de la estadística a 43 docentes de distintos países de Latinoamérica y de las tres etapas, con cuatro ítems vinculados con nuestro objetivo. A partir del análisis cuantitativo y cualitativo de dichos ítems, se han obtenido los siguientes resultados: a) respecto a la preparación, mientras que los datos cuantitativos muestran una autovaloración positiva, sin diferencias estadísticamente significativas entre etapas, los datos cualitativos evidencian una formación inicial escasa o nula; b) respecto a los conocimientos centrales, se ha identificado un enfoque polifacético que integra la relevancia contextual, las metodologías activas, el desarrollo de competencias estadísticas específicas y la adaptación a las características del alumnado. Se concluye que estos datos aportan pistas para diseñar planes de desarrollo profesional del profesor en estadística que permitan implementar tareas de estadística de manera fundamentada.

Palabras clave: Alfabetización estadística, Desarrollo profesional del profesorado de matemáticas, Educación estadística, Enseñanza de la estadística.

 

Resumo

O objetivo deste artigo é explorar a autoavaliação da prontidão e do conhecimento básico dos professores da educação infantil, do ensino fundamental e do ensino médio para ensinar estatística, como ponto de partida para a elaboração de planos de treinamento em serviço no ensino de estatística. Como preâmbulo, são revisados alguns marcos que conceituam a atividade profissional do professorado em estatística e as ideias centrais da estatística para o seu ensino. Os dados foram obtidos por meio da aplicação de um questionário online sobre ensino. a 43 professores de diferentes países da América Latina e das três etapas, com quatro itens relacionados ao nosso objetivo. A partir da análise quantitativa e qualitativa desses itens, foram obtidos os seguintes resultados: a) com relação à preparação, enquanto os dados quantitativos mostram uma autoavaliação positiva, sem diferenças estatisticamente significativas entre os estágios, os dados qualitativos mostram pouca ou nenhuma formação inicial; b) com relação ao conhecimento básico, foi identificada uma abordagem multifacetada que integra relevância contextual, metodologias ativas, desenvolvimento de competências estatísticas específicas e adaptação às características dos alunos. Conclui-se que esses dados fornecem pistas para a elaboração de planos de treinamento contínuo que permitam a implementação de tarefas estatísticas de forma bem fundamentada.

Palavras-chave: Desenvolvimento profissional de professores de matemática, Educação estatística, Ensino de estatística, Formação em serviço, Letramento estatístico.

 

Abstract

The aim of this article is to explore the self-assessment of the preparation and core knowledge for teaching statistics of in-service teachers in pre-primary, primary and secondary education, as a starting point for the design of in-service training plans in statistical education. As a preamble, some frameworks that conceptualize teachers’ professional activity and the core ideas of statistics for teaching are reviewed. In order to obtain data, an online questionnaire on statistics teaching was administered to 43 teachers from different Latin American countries and from the three stages, with four items linked to our objective. From the quantitative and qualitative analysis of these items, the following results were obtained: a) with regard to preparation, while the quantitative data show a positive self-assessment, with no statistically significant differences between stages, the qualitative data show little or no initial education; b) with regard to core knowledge, a multifaceted approach was identified that integrates contextual relevance, active methodologies, the development of specific statistical competences and adaptation to the characteristics of the students. It is concluded that these data provide clues for the design of continuous education plans that allow the implementation of statistical tasks in a well-founded manner.

Keywords: In-service training, Professional development of mathematics teachers, Statistical education, Statistical literacy, Teaching statistics.

 

Recibido: 12/07/2024 - Aceptado: 18/05/2025

 

1. INTRODUCCIÓN

 

La mayoría de los estudios sobre el conocimiento del profesorado en activo para enseñar estadística revela que posee escasos conocimientos en diversos subdominios o facetas, tal como se ha evidenciado en la revisión sistemática realizada por Franco y Alsina (2022a).

En el caso del profesorado de infantil y primaria, diversos autores (Estrella et al., 2015; Koleza y Kontogianni, 2012; Siswono et al., 2018; Watson et al., 2008), han hecho alusión a la falta de dominio para enseñar estadística, debido en buena medida a una escasa o nula formación inicial ya que es muy reciente la incorporación de este estándar de contenidos en el currículo vigente. En este sentido, Vásquez y Alsina (2022) señalan que, si bien la incorporación de contenidos vinculados al estudio de la estadística en los planes de estudio se remonta al año 1923 cuando el National Committee on Mathematical Requirements of the Mathematical Association of America recomienda por primera vez el estudio de la estadística en los grados 7-12 (correspondientes a 12-17 años) en The Reorganization of Mathematics in Secondary Education (NCRM, 1923), no es hasta finales de la década de los 80 del siglo XX cuando el National Council Teachers of Mathematics (NCTM), hace notar la necesidad de que los estudiantes de los grados K-12 (4-16 años) comprendan el sentido de los datos y, de este modo, favorecer el desarrollo de su conciencia social (NCTM, 1989). Para esto, proponen abordar temas de estadística y probabilidad como un eje de contenidos. Algunos años más tarde, este planteamiento se ve reforzado en los Principles and Standards for School Mathematics (NCTM, 2003), adelantando el estudio de este estándar de contenido desde los tres años.

En el caso del profesorado de secundaria de matemáticas, por un lado, la literatura señala la escasez de formación específica sobre didáctica de la estadística (Rodríguez-Muñiz et al., 2022); y, por otro lado, el efecto positivo de las actividades de formación en su conocimiento tanto disciplinar (Balduino et al., 2021) como didáctico (Fernández et al., 2020; Schoen et al., 2019), además de destacar la necesidad de considerar la tecnología como parte del conocimiento del profesorado (Muñiz-Rodríguez y Rodríguez-Muñiz, 2021).

Todos estos antecedentes conllevan, en el profesorado en activo de las distintas etapas, inseguridades y miedos para enseñar estadística, lo cual ocasiona o bien la omisión de la enseñanza o bien una enseñanza poco eficaz (Vásquez y Alsina, 2023), en el sentido de que contribuye muy poco al desarrollo de la alfabetización estadística (Gal, 2002, 2005, 2012) o, más en general, del sentido estocástico (Batanero, 2004). Para mejorar esta situación, es evidente que hace falta que las administraciones educativas de los distintos países tomen decisiones en torno al desarrollo profesional del profesorado orientadas a impulsar planes que permitan actualizar el conocimiento del profesorado de las diferentes etapas educativas sobre la educación estadística.

Desde este punto de vista, este artículo pretende indagar respecto al desarrollo profesional en educación estadística que ha recibido el profesorado en activo de las diferentes etapas educativas. En concreto, a partir de la administración de un cuestionario online, el objetivo de este artículo es examinar y aportar evidencias sobre la autovaloración del profesorado de educación infantil, primaria y secundaria en relación con la formación recibida para la enseñanza de la estadística; y, por otro lado, identificar los conocimientos e ideas que consideran más relevantes para fomentar un aprendizaje eficaz de esta disciplina en el aula escolar como punto de partida para, posteriormente, poder diseñar una hoja de ruta a partir de las posibles lagunas identificadas.

 

2. MARCOS SOBRE EL CONOCIMIENTO PROFESIONAL EN ESTADÍSTICA DEL PROFESORADO

 

Los programas de desarrollo profesional del profesorado de matemáticas suelen enfocarse en fortalecer el conocimiento del contenido, la pedagogía y la práctica del profesorado con el objetivo de mejorar la enseñanza y los resultados de los estudiantes. La inclusión de la estadística en el currículo de todos los niveles ha traído como consecuencia la necesidad de que los programas de formación incluyan este contenido de manera que el profesorado adquiera el conocimiento para llevar a cabo la tarea de enseñar estadística. Pero surge la pregunta ¿Qué quiere decir que el profesor tenga dicho conocimiento? En respuesta, desde finales del siglo pasado, se han creado algunos marcos que tratan de conceptualizar el conocimiento profesional del profesorado que enseña estadística (Figura 1).

Conviene desde ahora aclarar que en este estudio nos referimos a la estadística sin hacer un seguimiento específico de la probabilidad. Aunque muchos autores la incluyen cuando se refieren a la estadística, otros establecen una separación entre ambas como objeto de estudio. Asumiendo la íntima relación que existe entre la estadística y la probabilidad, pero manteniendo el foco en la primera, la decisión metodológica que se ha tomado es mencionar a la probabilidad cuando así lo hagan las fuentes consultadas, pero sin pretender abordar o cubrir la problemática de esta herramienta.

 

Figura 1

Evolución de marcos que buscan conceptualizar el conocimiento profesional del profesorado que enseña estadística.

 

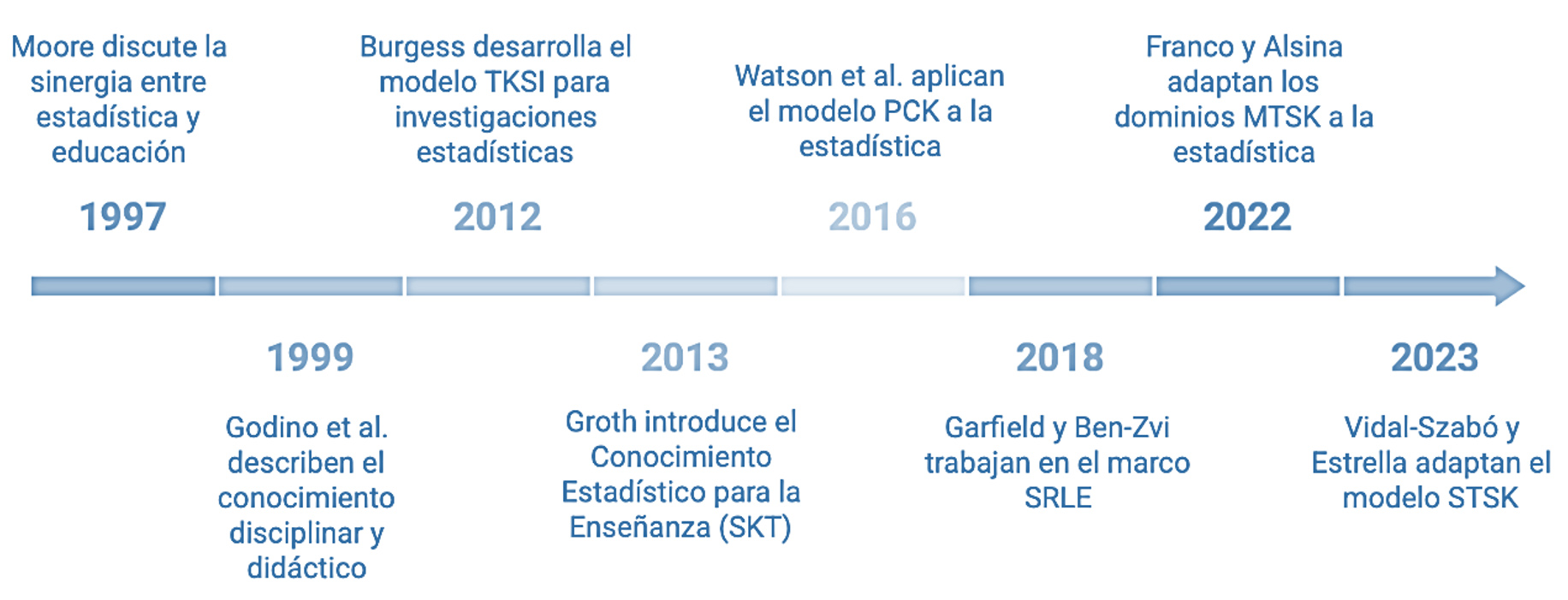
Moore (1997), por ejemplo, señala que la enseñanza de estos temas requiere la activación conjunta del contenido, la pedagogía y la tecnología, siendo esta última un elemento fundamental, ya que está directamente vinculada al contenido y a la pedagogía al facilitar, mediante el uso de herramientas tecnológicas, aspectos como la visualización, la resolución de problemas, el uso de diversas representaciones, simulaciones, entre otros (Figura 2).

 

Figura 2

Sinergia entre estadística y educación estadística.

 

• Contenido ⟷ Pedagogía

Análisis de datos ⟷ Trabajo práctico

Estadística en la práctica ⟷ Comunicación, cooperación

Más conceptos ⟷ Menos demostraciones

• Pedagogía ⟷ Tecnología

Visualización ⟷ Automatización de gráficos

Resolución de problemas ⟷ Automatización de cálculos

Aprendizaje activo ⟷ Multimedia

• Tecnología ⟷ Contenido

Computación ⟷ Análisis de datos, diagnósticos, bootstrap, ...

Automatización ⟷ Más conceptos

Simulación ⟷ Menos demostraciones

Fuente: Moore (1997, p. 129) [Transcripción y traducción de los autores].

 

 

Godino et al. (1999) describen el conocimiento disciplinar y didáctico involucrado en la enseñanza de la estadística, junto con la probabilidad, considerando los siguientes componentes: a) reflexión epistemológica; b) transformación y adaptación de los objetos matemáticos a un nivel educativo específico; c) conocimiento de las dificultades, obstáculos y errores que enfrentan los estudiantes al aprender, así como de las estrategias utilizadas para resolver problemas; y d) ejemplificación de situaciones didácticas, metodologías de enseñanza y recursos didácticos adecuados para la enseñanza de estadística, incluyendo el uso de tecnología. Más adelante, Godino et al. (2008) refinaron este modelo creando lo que denominan conocimiento pedagógico estadístico, que consta de cinco componentes: epistemológico, cognitivo, afectivo, interaccional y de recursos y técnicas de enseñanza.

Watson y colaboradores (Callingham et al., 2016; Callingham y Watson, 2011; Watson et al., 2009) aplican el modelo de Conocimiento Pedagógico del Contenido (PCK) a la estadística, enfatizando la capacidad del profesorado para anticipar las respuestas de los estudiantes, diseñar estrategias didácticas efectivas y evaluar el aprendizaje. Identifican cuatro niveles de desarrollo del PCK, desde un nivel consciente hasta uno completo, donde los profesores integran conocimiento estadístico y estrategias de intervención pedagógica. Este enfoque vincula la teoría con la práctica para promover una enseñanza más efectiva y adaptada a las necesidades del aula.

Asimismo, Burgess (2006, 2009, 2011, 2012), basándose en algunos de los componentes del MKT (Ball et al., 2008) y en el modelo para describir el pensamiento estadístico propuesto por Wild y Pfannkuch (1999), plantea que, dada la naturaleza única de la educación estadística, que demanda formas específicas de pensamiento y razonamiento, es necesario un modelo que distinga estas diferencias del pensamiento matemático en general (Burgess, 2009). En consecuencia, sugiere el modelo bidimensional TKSI (Teacher Knowledge of and for Statistical Investigations). En una dimensión vertical del modelo se consideran las componentes del pensamiento estadístico de Wild y Pfannkuch, mientras que en la dimensión horizontal se incluyen los tipos de conocimientos del profesor de acuerdo con el MKT. El modelo señala que al analizar el conocimiento del profesor es importante describir y reflexionar en cada entrada del cruce que especifica un componente del pensamiento estadístico junto con un tipo de conocimiento del profesor.

A su vez, Groth (2007, 2012, 2013) indaga en torno a la formación disciplinar que movilizan los docentes que enseñan estadística, introduciendo el concepto de Conocimiento Estadístico para la Enseñanza (Statistical Knowledge for Teaching, SKT). El SKT integra los modelos MKT y las KDU (Key Developmental Understandings), y propone que el conocimiento pedagógico y disciplinar no deben abordarse por separado, sino como un proceso conjunto en el que el docente considera la perspectiva del estudiante.

El desarrollo del conocimiento pedagógico y disciplinar en la enseñanza de la estadística se basa en la transformación de las comprensiones clave del desarrollo (KDU) en ideas pedagógicamente poderosas. Este proceso requiere un descentramiento conceptual, en el cual las ideas personales se reformulan para ser utilizadas eficazmente en la enseñanza.

El conocimiento disciplinar (Subject Matter Knowledge) comprende tres dimensiones principales: el conocimiento común del contenido, el conocimiento especializado del contenido y el conocimiento del horizonte estadístico.

• El conocimiento común del contenido estadístico (Common Content Knowledge of statistics) incluye habilidades y conceptos estadísticos fundamentales, como el uso del significado empírico o frecuencial de la probabilidad.

• El conocimiento especializado del contenido estadístico (Specialized Knowledge of statistics) abarca competencias más específicas, como la capacidad de reconocer modificaciones no convencionales en representaciones estadísticas y el uso de gráficos de transición, como los diagramas de sombrero.

• El conocimiento del horizonte estadístico (Horizon Knowledge of statistics) se refiere a la comprensión de estructuras que permiten conectar diferentes niveles de conocimiento, como la similitud en las expresiones y el objetivo de la desviación media absoluta y la desviación estándar.

A partir de este conocimiento disciplinar, el conocimiento pedagógico del contenido (Pedagogical Content Knowledge, PCK) se construye mediante la integración de aspectos clave para la enseñanza. Este conocimiento pedagógico incluye:

• El conocimiento del contenido y los estudiantes (Knowledge of Content and Students, KCS), que implica entender cómo los estudiantes interpretan y utilizan herramientas estadísticas, por ejemplo, la manera en que leen diagramas de caja.

• El conocimiento del contenido y la enseñanza (Knowledge of Content and Teaching, KCT), que considera la necesidad de replantear estrategias de enseñanza tradicionales para favorecer el aprendizaje de razonamiento estocástico en lugar de enfoques deterministas.

• El conocimiento curricular, que requiere un descentramiento conceptual para integrar objetivos instruccionales y teorías del aprendizaje que pueden diferir de la propia perspectiva del docente (Groth, 2013, p. 143).

Por su parte, Garfield, Ben-Zvi y colaboradores (Ben-Zvi et al., 2018; Garfield y Ben-Zvi, 2008a, 2008b, 2009; Pfannkuch y Ben-Zvi, 2011) desarrollan un marco conceptual que orienta la formación docente, destacando la importancia de crear entornos educativos que promuevan el razonamiento estadístico como un proceso dinámico y fundamentado en la interacción activa con datos y contextos reales. A través de los Entornos de Aprendizaje del Razonamiento Estadístico (Statistical Reasoning Learning Environment, SRLE), que buscan fomentar el pensamiento y razonamiento estadístico en los estudiantes. Sus seis dimensiones interconectadas (Figura 4) incluyen el uso de datos reales, la integración de herramientas tecnológicas y la promoción de un discurso argumentativo en el aula. Consideran que estos principios deben aplicarse tanto en la formación inicial como en el desarrollo profesional de los profesores, asegurando que experimenten estos entornos para replicarlos en sus prácticas docentes de aula.

 

Figura 3

Red de dimensiones interrelacionadas de Statistical Reasoning Learning Environment.

Fuente: Ben-Zvi et al. (2018, p. 489). [Transcripción y traducción de los autores].

 

Más recientemente, Vidal-Szabó y Estrella (2020, 2023) adaptan el modelo MTSK (Carrillo et al., 2018) al ámbito de la estadística, dando lugar al modelo STSK (Statistics Teacher›s Specialised Knowledge). A través de este enfoque se busca caracterizar el conocimiento especializado necesario para que los profesores de matemática enseñen estadística, reconociendo la autonomía de la estadística como disciplina científica y educativa, separada de la matemática. Dicho modelo conserva los dominios de conocimiento estadístico (SK) y conocimiento didáctico del contenido (PCK), desglosados en subdominios como KoT (temas estadísticos), KSS (estructura estadística), KPS (práctica estadística), KST (enseñanza de la estadística), KFLS (características del aprendizaje) y KSLS (estándares de aprendizaje). Esta propuesta enfatiza la diferenciación entre la enseñanza de la estadística y la matemática, destacando a la estadística como un campo autónomo con enfoques propios como por ejemplo el ciclo PPDAC (Wild y Pfannkuch, 1999). Además, el modelo facilita la operacionalización del conocimiento especializado del profesorado, el diseño de propuestas didácticas basadas en datos reales y la superación de retos epistemológicos, cognitivos y didácticos, ofreciendo un marco teórico robusto para la educación estadística y contribuyendo al desarrollo profesional docente.

Finalmente, Franco y Alsina (2022b) adaptan los dominios y subdominios del MTSK (Carrillo et al., 2018) a la enseñanza de la estadística (Figura 4).

 

Figura 4

Adaptación del Modelo MTSK a la enseñanza de la estadística

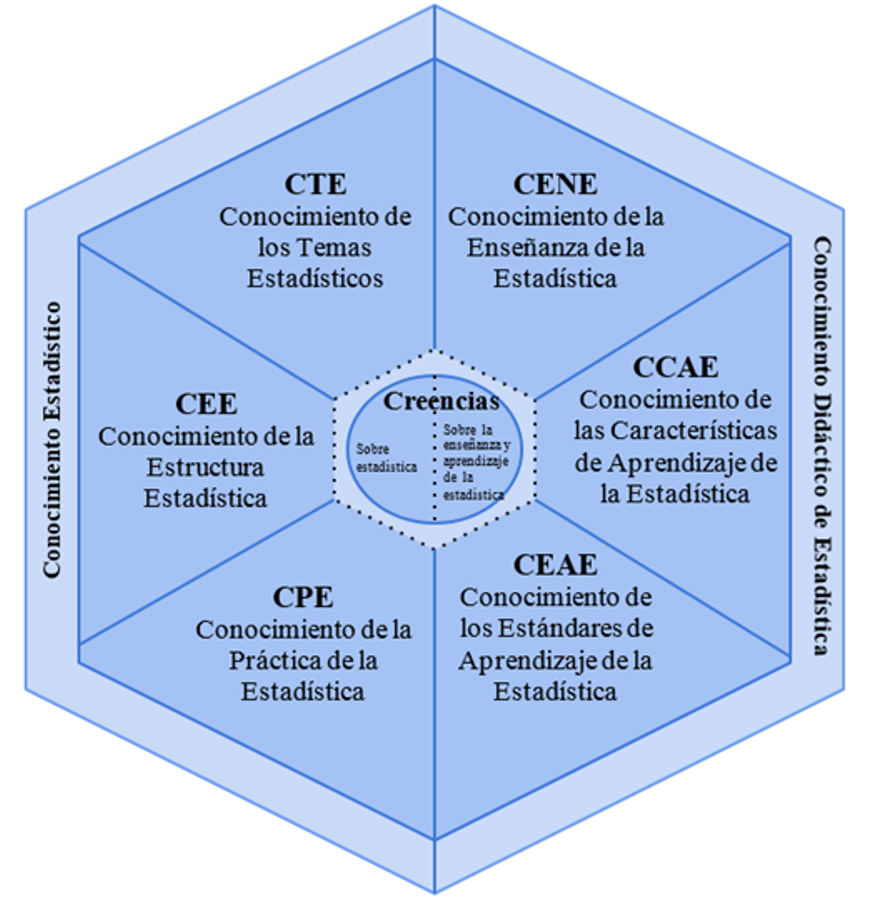
Fuente: Franco y Alsina (2022b, p. 70)

 

En esta adaptación, el dominio Conocimiento Estadístico (CE) contiene los subdominios: Conocimiento de los Temas Estadísticos (CTE), se focaliza en los aspectos fenomenológicos, significados y definiciones de conceptos, ejemplos, etc., que caracterizan aspectos concretos de la estadística (Ben-Zvi y Garfield, 2004); Conocimiento de la Estructura Estadística (CEE), abarca las distintas conexiones conceptuales, en el que el profesorado tiene que considerar las distintas medidas (centro, dispersión, forma, entre otras) y las distintas representaciones de datos bajo un contexto específico (Vidal-Szabó y Estrella, 2020); y Conocimiento de la Práctica de la Estadística (CPE), considera las distintas formas de conocer, crear o producir estadística a partir de los procesos de pensamiento involucrados en la resolución de problemas en los que pueden enfocarse los conocimientos estadísticos (Wild y Pfannkuch, 1999). Por su parte, el dominio Conocimiento Didáctico de Estadística (CDE) incluye los subdominios: Conocimiento de la Enseñanza de la Estadística (CENE), abarca las distintas estrategias que permiten al docente fomentar un desarrollo de las capacidades estadísticas, que dependen del conocimiento sobre el contenido estadístico (Batanero, 2009); Conocimiento de las Características de Aprendizaje de la Estadística (CCAE), hace referencia al proceso de comprensión de los estudiantes sobre los distintos contenidos, el lenguaje asociado a cada concepto estadístico, así como errores, dificultades u obstáculos posibles en el proceso de aprendizaje del alumnado (Yañez, 2016); y Conocimiento de los Estándares de Aprendizaje de la Estadística (CEAE), focaliza los contenidos estadísticos que se requieren enseñar en un nivel determinado, posibilitando la mejora de la práctica del profesorado que enseña estadística (NCTM, 2003).

Desde una perspectiva global, estos distintos marcos ofrecen una diversidad de perspectivas teóricas, integrando componentes epistemológicos, cognitivos y tecnológicos, resaltando la interacción entre contenido, pedagogía y herramientas didácticas. Reflejando una evolución hacia la sistematización y especialización del conocimiento necesario para enseñar estadística. Asimismo, se vislumbra la necesidad de formar al profesorado para una comprensión profunda y reflexiva del conocimiento estadístico, anclado en prácticas reales y teorías actualizadas.

 

3. CONOCIMIENTO E IDEAS ESTADÍSTICAS ESENCIALES PARA LA ENSEÑANZA

 

La estadística es una disciplina científica autónoma que surge a partir de diversas ciencias que se apoyan en la matemática, y cuenta con métodos propios de razonamiento (Moore, 1990). Pero ¿cómo llevar al aula escolar el estudio de la estadística? ¿Por dónde comenzar? ¿cuáles son las grandes ideas generadoras de aprendizaje en los temas de estadística? ¿Cómo evolucionan estas ideas? ¿Cuáles son las rutas típicas que considerar para la enseñanza y el aprendizaje de la estadística en el aula escolar?

En las últimas décadas, la educación estadística ha recibido una fuerte y creciente valoración, lo que ha impulsado reformas curriculares enfocadas en su enseñanza en el ámbito escolar. Este enfoque ha sido adoptado por numerosos países, los cuales han integrado contenidos relacionados con la estadística dentro del currículo de matemáticas. Esta incorporación abarca un desarrollo progresivo, que se inicia en las primeras edades con conocimientos emergentes vinculados a las ideas numéricas y de conteo propias de la edad, para luego ir progresando y enriqueciéndose a medida que los estudiantes avanzan en su etapa escolar, hasta llegar al abordaje de temas avanzados como la inferencia estadística (Vásquez y Cabrera, 2022).

Sin duda, es prioritaria una enseñanza progresiva de la estadística en las aulas a fin de desarrollar en los estudiantes las competencias necesarias para interpretar y analizar datos, formular conjeturas, tomar decisiones informadas y comunicar fenómenos aleatorios (Alsina, 2012; Vásquez et al., 2018). A este respecto, el Comité Español de Matemáticas (CEMat, 2021) enfatiza que este desarrollo debe comenzar desde edades tempranas y girar en torno a las ideas fundamentales de distribución, inferencia y predictibilidad e incertidumbre, que deben estar presentes en todas las etapas educativas.

Ello con el propósito de desarrollar el sentido estocástico, definido como:

la capacidad para hacer frente a una amplia gama de situaciones cotidianas que implican el razonamiento y la interpretación de datos, la elaboración de conjeturas y la toma de decisiones a partir de la información estadística, su valoración crítica y la comprensión y comunicación de fenómenos aleatorios, y la capacidad de realizar algunas predicciones (CEMat, 2021, p. 35).

Para atender a dicho propósito, el CEMat propone que los estudiantes realicen investigaciones estadísticas simples en contextos variados, como medios de comunicación, tecnología, deportes y juegos. Además, subraya el uso de herramientas tecnológicas para analizar y representar datos, realizar simulaciones y evaluar críticamente la información, promoviendo debates y una comunicación efectiva de conclusiones. En otro reciente informe sobre la situación de la competencia matemática en el ámbito español (en muchos aspectos, extrapolable al ámbito latinoamericano), el CEMat (2024) insiste en que la ampliación de los contenidos sobre sentido estocástico y su conexión con otros nuevos contenidos como el pensamiento computacional “requieren ampliar la formación del futuro maestro, en comparación a la actual” (p. 29).

Por su parte, Vásquez y Cabrera (2022) analizan de manera detallada la presencia de las ideas estadísticas fundamentales presentes en los currículos de matemática para educación infantil y primaria de diversos países, considerados referentes a nivel internacional, como Australia, España, Nueva Zelanda, y Singapur, entre otros. Para ello, se fundamentan desde la perspectiva de Burrill y Biehler (2011), quienes proponen un conjunto de ideas estadísticas fundamentales (datos, variación, distribución, representación de datos, asociación y correlación, probabilidad, muestreo e inferencia) que permiten transitar hacia “una comprensión más profunda a lo largo del tiempo a medida que los estudiantes maduran en su conocimiento de estadística” (Burrill y Biehler, 2011, p. 62) y que todo estudiante debería comprender al finalizar la educación secundaria. A partir de este análisis, identifican que, en la educación infantil, existe un mayor énfasis en las ideas de datos, representación de datos, variación, distribución, probabilidad y muestreo e inferencia. Estos temas se abordan de manera inicial, adaptándose a las características propias de la educación infantil, vinculándolos con conocimientos intuitivos y habilidades numéricas básicas. A medida que los estudiantes avanzan, estos conceptos se profundizan progresivamente. En la educación primaria, las ideas clave son similares, aunque el énfasis varía. Las ideas más destacadas, son datos, representación de datos, variación, probabilidad, distribución, muestreo e inferencia, y finalmente, asociación y correlación. Al igual que en la etapa de infantil, el tratamiento de estas ideas se ajusta a la edad y desarrollo de los estudiantes, aumentando en complejidad de forma gradual. Finalmente, se observa que las ideas de datos y representación de datos tienen mayor presencia en los currículos estudiados. Esto podría explicarse porque la enseñanza de la estadística se orienta principalmente hacia la resolución de problemas estadísticos y al desarrollo de competencias que permitan a los estudiantes interpretar información estadística en contextos cotidianos.

Por lo tanto, es fundamental que el profesorado comprenda y maneje estas ideas para adaptarlas de manera adecuada a los niveles de desarrollo de sus estudiantes. A su vez, estas nociones fundamentales deben integrarse en un proceso gradual y progresivo que comience en las primeras edades y se profundice a lo largo de toda la etapa escolar. El reciente Manifiesto a favor de la Alfabetización Estadística (AA. VV., 2024) refleja la preocupación de diversos colectivos docentes e investigadores y sociedades científicas por la necesidad de esta integración en el sistema educativo, con el objetivo de dotar a la ciudadanía de herramientas que le permitan desenvolverse en un mundo gobernado por los datos.

 

4. METODOLOGÍA

 

Este estudio se enmarca dentro de un enfoque metodológico mixto (Cohen et al., 2018), que resulta adecuado para examinar y aportar evidencias sobre la valoración del profesorado de educación infantil, primaria y secundaria en relación con la formación recibida para la enseñanza de la estadística, así como identificar los conocimientos e ideas que consideran más relevantes para fomentar un aprendizaje eficaz de esta disciplina en el aula escolar.

 

4.1. Participantes

 

La muestra participante es no probabilística y está compuesta por 43 docentes de educación infantil, primaria y secundaria de diferentes países de Latinoamérica (Tabla 1).

 

Tabla 1

Docentes participantes en el estudio

País	Nivel educativo en el que enseña			Totales
	Infantil	Primaria	Secundaria
Argentina	1	2	4	7
Bolivia	1	0	0	1
Brasil	2	0	3	5
Chile	3	20	3	26
México	0	1	0	1
Perú	1	1	1	3
Totales	8	24	11	43

Como se observa, se trata de una muestra diversa en cuanto a país de procedencia. Cabe señalar que más de la mitad de los participantes (n = 26; 60,5 %) ejercen en Chile. Esta sobrerrepresentación se debe al mayor alcance del cuestionario en redes académicas y profesionales del país, lo que constituye una limitación en términos de equilibrio muestral. No obstante, este estudio no busca la generalización estadística, sino ofrecer una aproximación exploratoria a percepciones y conocimientos docentes en diferentes contextos.

En lo que respecta a los años de experiencia docente de la muestra participante, un 27,9 % cuenta con hasta 5 años de experiencia, un 16,3 % tiene entre 6 a 10 años de experiencia y un 55,8 % tiene más de 10 años de experiencia en aula, lo cual permite recoger voces de profesionales con trayectorias variadas. En cuanto al género, esta variable fue registrada de forma opcional y no por todos los participantes, por lo que no se presenta un análisis detallado en este estudio.

 

4.2. Instrumento

 

Se elaboró un cuestionario de 12 preguntas (véase la Tabla 2), organizadas en cuatro dimensiones que se relacionan con los elementos de los marcos expuestos arriba como se expone a continuación. La primera dimensión, “Percepciones y valoraciones sobre la enseñanza de la estadística”, incluye dos preguntas abiertas que se refieren al conocimiento de la enseñanza de la estadística (Vidal-Szabó y Estrella 2020, 2023). La segunda dimensión, “Valoración sobre la preparación para la enseñanza de la estadística”, está formada por una pregunta de tipo Likert y una pregunta abierta que trata sobre la autoeficacia y la evaluación de la formación recibida (Garfield y Ben-Zvi, 2008b). La tercera dimensión, “Conocimientos centrales en la enseñanza de la estadística”, contiene dos preguntas abiertas sobre conocimiento del contenido estadístico (Groth, 2007). La cuarta dimensión, “Prácticas para guiar el aprendizaje de la estadística” agrupa seis preguntas abiertas sobre recursos para la enseñanza (Godino et al., 2008), Conocimiento de los estudiantes y la enseñanza (Groth, 2007, 2012, 2013) y Conocimiento de prácticas (Vidal-Szabó y Estrella, 2020, 2023).

El cuestionario fue sometido a una validación de contenido por juicio de tres expertos, con experiencia en educación estadística y formación del profesorado. A partir de sus observaciones, se realizaron ajustes que mejoraron la claridad, pertinencia y coherencia de los ítems con las dimensiones teóricas. Posteriormente, se llevó a cabo una aplicación piloto con un grupo de estudiantes con características similares a la muestra principal. Esta fase permitió calibrar el instrumento, es decir, ajustar el lenguaje y la secuencia de las preguntas para asegurar una comprensión adecuada.

 

4.3. Obtención de datos

 

Para recopilar los datos, se ha realizado una invitación abierta a profesores a través de redes sociales para responder un cuestionario en línea, a través de Google Forms, sobre la enseñanza de la estadística.

Las preguntas han sido diseñadas y calibradas por los investigadores del estudio, demandan entregar una respuesta escrita y requieren de 15 a 20 minutos para ser respondidas.

 

Tabla 2

Dimensiones y preguntas que conforman el cuestionario

Dimensión	Preguntas (ítems)
Percepciones y valoraciones sobre la enseñanza de la estadística	2. ¿Por qué consideras importante enseñar estadística? ¿Para qué sirve su enseñanza? 7. ¿Consideras que la ciudadanía está, en su conjunto, alfabetizada estadísticamente? ¿Por qué?
Valoración sobre la preparación para la enseñanza de la estadística	3. En una escala del 1 al 10, donde 1 = muy mal preparado y 10 = muy bien preparado, ¿cómo te sientes de preparado para la enseñanza de la estadística en el aula escolar? 4. ¿Cómo valoras la formación inicial o continua que has tenido para enseñar estadística?
Conocimientos centrales en la enseñanza de la estadística	1. Escribe algunas palabras (ideas/conocimientos clave) que piensas están asociadas a la enseñanza de la estadística en el aula escolar. 5. Si enseñas o tuvieras que enseñar estadística, ¿qué es lo más importante?, ¿en qué te focalizarías?
Prácticas para guiar el aprendizaje de la estadística	6. ¿Qué contextos o recursos de enseñanza utilizas o utilizarías para enseñar estadística? 8. Cuando los alumnos recogen datos de un contexto real, ¿clasifican los datos de alguna manera o se les dan los datos organizados?; en el primer caso, ¿cómo lo hacen para clasificarlos? 9. ¿Hacen el recuento de los datos clasificados o se les da el recuento hecho?; en el primer caso, ¿de qué manera hacen el recuento? 10. ¿Escriben de alguna manera el resultado del recuento? En caso afirmativo, ¿cómo? 11. ¿Cómo representan los datos que se les proporcionan o que han obtenido a partir de un recuento? 12. ¿Interpretan de alguna manera los datos o tú, como docente, haces una interpretación final? En el primer caso, ¿cómo los interpretan?

Tomando en consideración nuestro objetivo, en este artículo se han analizado las dimensiones “Valoración sobre la preparación para la enseñanza de la estadística” (ítems 3 y 4) y “Conocimientos centrales en la enseñanza de la estadística” (ítems 1 y 5).

 

4.4. Procedimiento de análisis de datos

 

En lo que respecta al análisis de los datos, se ha realizado un análisis cuantitativo y cualitativo, en correspondencia con el enfoque adoptado en este estudio. El análisis cuantitativo ha considerado un análisis descriptivo por medio de resúmenes estadísticos de las puntuaciones otorgadas por los docentes en el ítem 3 del cuestionario. Asimismo, se aplicó un análisis de la varianza (ANOVA) para examinar si existen diferencias estadísticamente significativas en los niveles de preparación percibidos para la enseñanza de la estadística en los profesores de educación infantil, primaria y secundaria. Para tal análisis se utilizó el software SPSS v.27. Por su parte, el análisis cualitativo respondió a las características específicas de cada ítem, y ha seguido procedimientos diferenciados en función del tipo de pregunta a analizar. En el caso del ítem 1, se aplicó un análisis exploratorio de frecuencias léxicas por medio de una nube de palabras creada a través del software WordArt.com, eliminando palabras funcionales con el fin de visualizar más limpiamente los términos recurrentes asociados a la enseñanza de la estadística. Dicho análisis permitió alcanzar una primera aproximación a los conceptos movilizados por el profesorado. En cambio, para los ítems 4 y 5, que solicitaban respuestas más extensas y argumentadas, se empleó un análisis temático con enfoque inductivo, que siguió los procedimientos de codificación abierta (Miles et al., 2020) que se indican a continuación: 1) lectura general de las respuestas -que corresponden a las unidades de análisis-, para tener una imagen global de estas en su conjunto; 2) bitácoras con registros de las impresiones y los principales temas encontrados, para identificar códigos de respuestas que se han agrupado en categorías preliminares de análisis de acuerdo con su similitud, para luego levantar categorías de; 3) matriz consolidada de datos, para establecer inferencias, saturación y conclusiones y, de este modo, captar el sentido general de las respuestas y establecer algunas reflexiones.

El proceso de codificación fue realizado de manera independiente por dos de los autores del estudio. En una primera fase, ambos realizaron una lectura general de las respuestas y desarrollaron registros preliminares. Posteriormente, se generaron códigos que fueron agrupados en categorías temáticas, las cuales fueron discutidas hasta alcanzar consenso. De este modo, a través de la triangulación entre ambos investigadores se garantizó la objetividad, la coherencia y validez interna del análisis cualitativo, procurando minimizar la influencia de sesgos individuales en la interpretación de los datos.

Cabe precisar que en el análisis del ítem 4, se realizó una categorización no excluyente, en tanto las respuestas del profesorado solían centrarse simultáneamente en diversos aspectos formativos, que se entrelazan en su experiencia profesional. En contraste, para el ítem 5 se optó por una categorización excluyente, considerando el aspecto predominante en cada respuesta. Esta decisión se fundamenta en que dicho ítem apuntaba a identificar aspectos en los que se focalizaría el docente de manera prioritaria al enseñar estadística. De este modo, a través de dicha distinción metodológica se busca preservar la especificidad interpretativa de cada dimensión analizada.

 

5. RESULTADOS

 

5.1. Valoración sobre la preparación para la enseñanza de la estadística

 

En primer lugar, al analizar las respuestas del ítem 3 del cuestionario “En una escala del 1 al 10, donde 1 = muy mal preparado y 10 = muy bien preparado, ¿cómo te sientes de preparado para la enseñanza de la estadística en el aula escolar?”, se observa que las puntuaciones se distribuyen según el nivel educativo como se muestra en la Figura 5 y en la Tabla 3.

 

Figura 5

Niveles de preparación percibidos por profesores de educación infantil, primaria y secundaria

 

Tabla 3

Resúmenes estadísticos de las puntuaciones según etapa educativa

Etapa educativa	Media	Varianza	Rango	Mediana	Mínimo	Máximo
Educación Infantil	6,38	3,13	5	6	4	9
Educación Primaria	6,62	2,68	6	7	4	10
Educación Secundaria	6,82	2,76	4	7	5	10

A partir de los datos se observa que las medias y las medianas son similares, con valores cercanos a 6.5 en las tres etapas, y las varianzas también son comparables, lo que indica consistencia en las respuestas. El rango intercuartílico, también comparable entre los grupos, con una ligera mayor dispersión en el caso de los profesores de primaria (de 5,5 a 8) en comparación con el profesorado de infantil y secundaria. La variabilidad total es moderada, siendo el grupo de profesores de primaria el que presenta una mayor amplitud en las respuestas (de 4 a 10). En general, los resultados sugieren percepciones homogéneas sobre los niveles de preparación para la enseñanza de la estadística entre los tres niveles educativos.

Estos datos, que son normales, se corroboran con el análisis ANOVA (Tabla 4) que muestra que no existen diferencias estadísticamente significativas en los niveles de preparación percibidos para la enseñanza de la estadística en los profesores de educación infantil, primaria y secundaria.

 

Tabla 4

Resultados análisis ANOVA

Origen de las variaciones	Suma de cuadrados	Grados de libertad	Promedio de los cuadrados	F	p-valor	Valor crítico para F
Entre grupos	0,91	2	0,46	0,16	0,85	3,23
Dentro de los grupos	111,14	40	2,78
Total	112,05	42

 

El estadístico F (0,16) y el valor p (0,85) confirman que las diferencias observadas entre los grupos no son significativas. Además, la mayor parte de la variación proviene de dentro de los grupos (111,14 de un total de 112,05), y el valor crítico para F (3,23) refuerza esta conclusión. Por lo tanto, no se identifican discrepancias significativas en la percepción de preparación entre los niveles educativos.

En segundo lugar, al analizar de manera global las respuestas otorgadas al ítem 4 “¿Cómo valoras la formación inicial o continua que has tenido para enseñar estadística?”, emergen de mayor a menor predominancia cuatro grandes temas como categorías de respuesta: insuficiencia en la formación inicial, falta de formación práctica, necesidad de mayor enfoque en estadística y formación continua como recurso. Conviene aclarar que el tratamiento de datos se hizo tomando a las respuestas de los profesores como las unidades de análisis, mismas que se compararon y codificaron para formar grupos con rasgos comunes; cada grupo dio lugar a uno de los temas que se describen en seguida. Es claro que los temas están relacionados entre sí, por lo que una respuesta podría caer en dos o más temas, no obstante, se consideró el rasgo más destacado en cada respuesta.

Insuficiencia de la formación inicial

Este es el tema más predominante, porque ocurrió con más frecuencia, y refleja una percepción generalizada de que la formación inicial en educación estadística es insuficiente. Los participantes describen su formación como básica, débil, escasa, o incluso nula. Hay una sensación clara de que la preparación inicial no proporciona las herramientas necesarias para enseñar estadística de manera efectiva. Los siguientes enunciados son opiniones de los profesores sobre la formación inicial en estadística (identificamos el profesorado mediante la notación: P1, P2, ..., P43):

P1	La valoro como básica y debe tener un mayor énfasis para desarrollar las habilidades matemáticas en los niños.
P5	Nula. No he tenido solo autodidacta.
P7	Mi formación inicial sobre estadística fue muy escasa y continua no he tenido, salvo aquella que he buscado de manera personal para realizar actividades con los estudiantes.
P6	Débil.
P39	No he recibido formación inicial ni continua al respecto, acá en Bolivia es un tema muy olvidado, por lo general la enseñanza se centra en números.

 

Falta de formación práctica

 

El segundo tema relevante se refiere a la falta de un enfoque práctico en la formación inicial y continua. Aunque algunos docentes mencionan haber recibido formación teórica en estadística, esta no incluyó la enseñanza práctica ni estrategias para aplicar este conocimiento en el aula. La carencia de formación práctica se menciona como un obstáculo significativo para enseñar estadística. Las siguientes opiniones se refieren a la formación práctica recibida:

P30	Difícil, falta tiempo para crear material lúdico.
P29	La formación inicial no es suficiente, se debe desarrollar el conocimiento y la estrategia con la experiencia de la enseñanza y capacitaciones.
P20	Desde la sinceridad, siento que la formación inicial fue débil en este contenido y la formación continua que he tenido se ha basado en matemáticas general.
P10	Muy básico, pero por la cantidad de actividades.
P4	El fuerte fue cálculo y álgebra, pero no estadística.

 

Escasa atención a la estadística en la formación docente

 

El tercer tema relevante es la percepción de que la estadística no recibe la atención suficiente en los programas de formación docente. Los participantes consideran que la estadística es un área importante, especialmente en el contexto actual, y sienten que debería tener un mayor énfasis en la formación de profesores para que estos estén mejor preparados para enseñarla a los niños.

P3	Considero que no se le ha entregado la suficiente importancia considerando la necesidad actual en nuestra sociedad.
P38	Creo que tanto la formación inicial, como la continua, le dan poca importancia a la estadística, lo que se traduce en docentes con preparación básica en esta área.
P28	Cuando egresé de la universidad, no se daba mucha importancia a la enseñanza de la estadística en el aula, creo que ahora se le está enseñando a los futuros profesores lo importante que es la enseñanza de la estadística para lograr un análisis de los datos y tomar decisiones en base a lo obtenido.
P33	Acho de extrema importância. Visto que durante a graduação há pouco disciplinas que discutem sobre o assunto.
P35	Ha sido muy escasa y se ha priorizado otras áreas de la matemática. Inclusive por el tiempo no podemos ver algún tema matemático dejamos de lado la estadística.

 

Formación continua como recurso

 

El tema menos tratado, aunque aún significativo, es la formación continua como un recurso que algunos docentes han utilizado para mejorar sus habilidades en la enseñanza de la estadística. Estos participantes han buscado activamente oportunidades adicionales de formación más allá de lo que recibieron en la universidad, ya sea a través de estudios de posgrado, talleres, o formación autodidacta. A continuación, se presentan algunas opiniones sobre la formación continua:

P14	Buscando aprimorar meus conhecimentos, fiz meu doutoramento nesta área e estudei sobre desenvolvimento e avaliação de projetos estatísticos. Aprendi muito e sigo estudando sempre.
P15	A Estatística começou a fazer parte da minha formação continuada, a partir do Mestrado.
P31	La valoro mucho ya que a través de las didácticas que nos enseñaron y desarrollo de las etapas se puede adaptar la enseñanza de la estadística a los diferentes niveles.
P39	Me pude formar después, gracias a la conectividad, pero faltan más capacitaciones, a nivel provincia al menos, sobre estas cuestiones.
P28	He tenido una buena preparación en lo que respecta a enseñar estadísticas en primer ciclo.

De este modo, a partir del análisis temático realizado para la pregunta 4, se evidencia que la percepción predominante entre los docentes en activo es que la formación inicial en estadística es insuficiente y carece de un enfoque práctico, lo que afecta su capacidad para enseñar eficazmente este contenido a los estudiantes. Además, hay un reconocimiento de la necesidad de dar mayor importancia a la estadística en la formación docente y un esfuerzo personal por parte de algunos docentes para compensar estas deficiencias a través de la formación continua. Estos temas destacan áreas críticas de mejora para los programas de formación docente, especialmente en la enseñanza de la estadística.

 

5.2. Conocimientos centrales en la enseñanza de la estadística

 

Primeramente, se han analizado las respuestas vinculadas al ítem 1 “Escribe algunas palabras (ideas/conocimientos clave) que piensas están asociadas a la enseñanza de la estadística en el aula escolar”. En la Figura 6 se presenta una nube de palabras elaborada con el software WordArt.com, a partir de la totalidad de respuestas recolectadas. Para su construcción, se eliminaron palabras funcionales (por ejemplo, conectores, artículos, preposiciones), lo que permitió visualizar los términos más recurrentes relacionados con las ideas y conocimientos clave asociados a la enseñanza de la estadística. Cabe señalar que la nube de palabras presentada corresponde al total de respuestas recolectadas, sin segmentación por nivel educativo. Esta decisión se tomó para poder ofrecer una visualización integrada de los términos más frecuentes. Sin embargo, como se detalla en los párrafos siguientes, el análisis cualitativo del contenido permitió identificar diferencias relevantes entre los niveles educativos, lo cual se expone en profundidad sin recurrir a representaciones visuales adicionales, para evitar redundancias y priorizar una interpretación más contextualizada de las ideas/conocimientos declarados.

 

Figura 6

Nube de palabras en relación con las ideas/conocimientos identificados

 

La nube de palabras muestra una visión general, sin distinción por etapa educativa. Sin embargo, a partir del análisis cualitativo del contenido de las respuestas, fue posible identificar ciertas tendencias diferenciales entre los niveles. Por ejemplo: en el caso de la educación infantil, se destaca la importancia de introducir en el registro y organización de datos de manera concreta y visual, fomentando la observación y la familiarización inicial con patrones y clasificaciones simples. En educación primaria, se prioriza la representación gráfica, el análisis y la comparación de datos, así como la cuantificación básica, lo que indica un enfoque en el desarrollo del pensamiento lógico, la representación e interpretación visual de los datos. Por último, en educación secundaria, el énfasis está en la aplicación de la estadística a la resolución de problemas provenientes de contextos reales, la interpretación avanzada de datos y la construcción de argumentaciones basadas en evidencia. Dichas ideas/conocimientos reflejan una evolución progresiva en el proceso de enseñanza y aprendizaje de la estadística adaptada a las necesidades de cada etapa educativa.

Si bien, en todos los niveles, hay un enfoque común que destaca la importancia del uso de datos, la representación gráfica y la organización e interpretación de información, conectando los aprendizajes con situaciones reales. También se evidencia un aumento en la complejidad y aplicabilidad de las ideas/conocimientos a medida que se avanza en etapa educativa. Así, en educación infantil, los términos reflejan un enfoque lúdico y concreto, centrado en actividades como el registro y la clasificación de datos en contextos reales. En primaria, se amplían los conceptos hacia la cuantificación, el análisis y el uso de gráficos y tablas, introduciendo una estructura más formal. En secundaria, las palabras destacan la profundización y abstracción, con énfasis en la aplicación, la argumentación y la alfabetización estadística, vinculando el aprendizaje a problemas del mundo real. Por tanto, estas diferencias sugieren una progresión en la complejidad de los conocimientos y prácticas vinculadas a la enseñanza de la estadística, desde una aproximación lúdica y contextualizada en infantil hasta un enfoque más aplicado y argumentativo en secundaria.

En segundo lugar, se han analizado las respuestas otorgadas al ítem 5 del cuestionario: “Si enseñas o tuvieras que enseñar estadística, ¿qué es lo más importante?, ¿en qué te focalizarías?”. Para este análisis se utilizó un enfoque cualitativo de tipo inductivo, mediante codificación abierta. Las unidades de análisis correspondieron a las respuestas individuales de los participantes, consideradas en su totalidad como unidades discursivas. Estas fueron comparadas, interpretadas y agrupadas con base en rasgos comunes, dando lugar a los temas emergentes que se describen a continuación. Cabe señalar que los temas identificados no son excluyentes entre sí, ya que las respuestas suelen abordar múltiples aspectos simultáneamente. Sin embargo, para efectos del análisis, cada respuesta fue clasificada según el aspecto predominante que reflejaba con mayor claridad su enfoque principal. De esta manera, los temas identificados se presentan ordenados según su frecuencia relativa porcentual en el conjunto de respuestas, entendida como el número de veces en que cada categoría fue reconocida como predominante en una respuesta. Aunque el análisis fue cualitativo, se estimó una frecuencia aproximada basada en la codificación temática. Los temas identificados, ordenados según su frecuencia de aparición en las respuestas, fueron los siguientes: (1) Uso de contextos reales para enseñar estadística (34,9%), destacando la importancia de vincular los aprendizajes con situaciones significativas para el estudiantado; (2) Métodos de formación y estrategias didácticas (27,9%), que incluyen la selección de recursos, tipos de tareas y enfoques participativos para guiar el aprendizaje; (3) Desarrollo de competencias estadísticas (20,9%), aludiendo a la capacidad de interpretar, analizar y comunicar información basada en datos; y (4) Adaptación a las características y necesidades del estudiante (16,3%), en relación con la atención a la diversidad y la personalización del proceso de enseñanza.

Estas cifras, si bien no derivan de un conteo automatizado, se corresponden con el análisis temático cualitativo presentado y con las expresiones utilizadas en el texto. 

Por otro lado, si bien este ítem fue inicialmente diseñado dentro de la dimensión “conocimientos centrales en la enseñanza de la estadística”, los resultados evidencian que muchas de las respuestas se vinculan más directamente con aspectos pedagógicos y didácticos, como la metodología de enseñanza y la intencionalidad educativa. Este hallazgo revela una visión integrada del conocimiento profesional docente, en la que los contenidos, las estrategias y las finalidades se entrelazan, especialmente en la percepción de docentes en formación o sin una formación especializada en estadística. Esta articulación entre lo disciplinar y lo pedagógico se retoma en la discusión del estudio como una característica relevante en los enfoques contemporáneos sobre el conocimiento para enseñar estadística.

 

Contextos reales para enseñar estadística

 

Esta categoría se refiere a la práctica de hacer que la estadística sea significativa y aplicable a la vida diaria de los estudiantes. La idea central es que los conceptos estadísticos deben ser presentados de manera que los estudiantes puedan ver su utilidad en situaciones reales, lo que facilita una comprensión más profunda y duradera.

La mayoría de los participantes han coincidido en la necesidad de conectar la estadística con contextos reales y utilizar datos de los propios estudiantes para hacer la materia más relevante y comprensible. Las siguientes dos opiniones van dirigidas en este sentido:

P32	Me focalizaría en enseñarla desde lo cotidiano relacionando la materia a su día a día, por ejemplo, votaciones para elegir la directiva del curso.
P31	Lo más importante es contextualizar la enseñanza a ejemplos más concretos y a experiencias de vida.

A partir de un análisis más detallado de las respuestas, es posible identificar algunos aspectos clave como:

• Uso de datos reales: Los docentes sugieren que los estudiantes trabajen con datos que ellos mismos recojan o que sean relevantes para su entorno, como encuestas sobre preferencias personales o datos de eventos escolares. Esto hace que la estadística no solo sea una teoría abstracta, sino una herramienta práctica para analizar información que les afecta directamente.

• Relevancia en la vida cotidiana: Relacionar la estadística con actividades y decisiones cotidianas, como votar en elecciones escolares o analizar resultados de encuestas simples, ayuda a los estudiantes a ver cómo la estadística puede ser útil en su vida diaria. Este enfoque también facilita la comprensión de conceptos complejos al conectarlos con experiencias conocidas.

 

Métodos de formación y estrategias didácticas

 

Esta categoría se centra en las técnicas y enfoques pedagógicos utilizados para enseñar estadística de manera efectiva. Incluye métodos que hacen el aprendizaje más interactivo, visual y participativo, con el objetivo de captar el interés de los estudiantes y facilitar su comprensión de los conceptos estadísticos. Muchas respuestas mencionan explícitamente el uso de métodos lúdicos, visuales y participativos, destacando la importancia de estos enfoques para captar el interés de los estudiantes y facilitar el aprendizaje. Las opiniones al respecto de dos profesores se presentan seguida continuación:

P16	Gráfico de doble entrada, con elementos de su interés.
P19	Observación de lo cotidiano, indagación, experimentación, juegos, gráficos, recolección y manejo e interpretación de datos.

Asimismo, dentro de las respuestas presentes en esta categoría es posible identificar algunos aspectos clave como:

• Métodos lúdicos y participativos: El uso de juegos y actividades prácticas es fundamental para hacer que la estadística sea accesible y atractiva. Las actividades que involucran a los estudiantes activamente pueden mejorar la retención y la comprensión de los conceptos estadísticos.

• Recursos visuales: La utilización de gráficos, diagramas coloridos y otros materiales visuales ayuda a los estudiantes a entender conceptos abstractos de manera concreta. Los gráficos grandes y visuales pueden ser especialmente efectivos en la enseñanza de estadísticas a estudiantes jóvenes.

 

Desarrollo de competencias estadísticas

 

Esta categoría se enfoca en el desarrollo de habilidades específicas relacionadas con la estadística. Se trata de enseñar a los estudiantes no solo los conceptos básicos de la estadística, sino también cómo aplicar estos conceptos para organizar, analizar e interpretar datos. Desde esta perspectiva, las respuestas de los participantes se han dirigido hacia la enseñanza de habilidades específicas relacionadas con la estadística como la organización de datos, la interpretación de gráficos y tablas y la comunicación de resultados. Las siguientes expresiones muestran dicho interés:

P7	Registro e interpretación de información en tablas de conteo.
P24	Conceptos básicos, conteo y comparación, experimentos simples, interpretación de resultados.

De manera más detallada, dentro de las respuestas presentes en esta categoría se han identificado diversos aspectos clave como:

• Habilidades prácticas: Los estudiantes deben aprender a recolectar, organizar, y analizar datos, así como a construir y leer gráficos y tablas. Estas habilidades son esenciales para aplicar la estadística en contextos reales.

• Aplicación de conceptos: Es importante que los estudiantes comprendan cómo los conceptos estadísticos se aplican a la resolución de problemas y la interpretación de datos en diversas situaciones.

Aunque este es un tema importante, se observa que es tratado con menos frecuencia en comparación con la contextualización y los métodos de formación y estrategias didácticas. Sin embargo, sigue siendo una parte clave del enfoque educativo.

 

Adaptación a la situación del estudiante

 

Esta categoría se refiere a la importancia de ajustar la enseñanza de la estadística según la edad, el nivel de desarrollo y el contexto de los estudiantes. La adaptación asegura que los contenidos sean apropiados y accesibles para el grupo de estudiantes al que se está dirigiendo. En este sentido, las respuestas de los participantes se han focalizado sobre todo en la necesidad de ajustar la enseñanza según la edad y el contexto de los estudiantes, asegurando que el contenido sea adecuado y accesible para su nivel de desarrollo; dos ejemplos se presentan en seguida:

P17	Que sea adecuada a la edad del estudiante.
P21	Lo más importante es poder organizar la información y acercar al niño al lenguaje matemático adecuado.

Finalmente, dentro de las respuestas en esta categoría se han identificado algunos aspectos clave como:

• Adecuación por edad: Los materiales y métodos deben ser adecuados para el nivel de desarrollo de los estudiantes, desde actividades simples para los más jóvenes hasta tareas más complejas para estudiantes mayores.

• Contexto del estudiante: Adaptar los ejemplos y actividades a las experiencias y el entorno de los estudiantes ayuda a que los conceptos sean más relevantes y comprensibles. Esto también puede incluir ajustar la complejidad de los problemas y las actividades según el grupo específico de estudiantes.

Este tema es mencionado, pero menos frecuentemente en comparación con los otros temas. La adaptación a la situación del estudiante es importante, pero se trata de una consideración complementaria a los enfoques más predominantes.

En síntesis, el análisis temático realizado sobre los conocimientos centrales de la educación estadística revela un enfoque multifacético que integra la relevancia contextual, metodologías pedagógicas efectivas, el desarrollo de competencias estadísticas específicas y la adaptación a las características del alumnado. Estos elementos son esenciales para lograr un aprendizaje significativo y eficiente en el campo de la estadística.

 

6. CONSIDERACIONES FINALES

 

En este artículo se ha explorado la autovaloración sobre la preparación y los conocimientos centrales para enseñar estadística del profesorado en activo de distintos países de Latinoamérica de las etapas de educación infantil, primaria y secundaria, con el propósito de tener una hoja de ruta para diseñar programas de formación continua del profesorado en educación estadística de todas las etapas.

Los hallazgos de esta investigación están limitados por la naturaleza exploratoria del enfoque experimental, que impide su generalización. Sin embargo, los datos obtenidos señalan algunas tendencias interesantes que deberían ser consideradas en futuras investigaciones. Un primer hallazgo del estudio es que, por un lado, el profesorado ha manifestado sentirse bien preparado para enseñar estadística, con valores cercanos a los 6,5 puntos en una escala de 10, sin que haya diferencias estadísticamente significativas entre las tres etapas educativas. A primera vista, pues, podría parecer que el profesorado moviliza conocimientos disciplinares y didácticos suficientes para enseñar estadística; sin embargo, la exploración cualitativa de la formación recibida, tanto inicial como continua, arroja datos muy diferentes, pues el profesorado ha manifestado de manera generalizada que la formación inicial recibida es insuficiente, utilizado calificativos como básica, débil, escasa o incluso nula. Señalan también otros aspectos como la falta de formación práctica para enseñar estadística en el aula, la escasa importancia que se da a la estadística en los programas de formación docente, en la línea identificada por Alsina y García-Alonso (2023) y Alsina et al. (2024), señalando la formación continua como vía de desarrollo profesional para superar estas lagunas. La contradicción identificada entre la percepción para enseñar estadística, que es positiva, y la formación previa recibida, que es negativa, podría estar indicando que, aunque el profesorado de las diferentes etapas educativas se sienta medianamente preparado para enseñar estadística, es poco probable de que sean conscientes del conjunto de dominios y subdominios descritos por los diferentes marcos teóricos que caracterizan los conocimientos para enseñar estadística (Burgess, 2006, 2009, 2011, 2012; Callingham et al., 2016; Callighan y Watson, 2011; Franco y Alsina, 2022b; Godino et al, 2008; Groth, 2007, 2012, 2013; Moore, 1997; Watson, 2001; Watson et al., 2008, 2009). Este primer hallazgo requiere que, dentro de la agenda de investigación sobre los conocimientos del profesorado para enseñar matemáticas, se inviertan esfuerzos para acordar cuales deberían ser los conocimientos centrales o ideas clave sobre la enseñanza de la estadística que se deberían asegurar en la formación continua.

Para empezar a indagar en torno a esta relevante cuestión, en este estudio hemos explorado, a través del análisis de los ítems 1 y 5 del cuestionario, los conocimientos que los docentes, desde la práctica, consideran centrales para enseñar estadística. Los datos obtenidos en esta dimensión muestran un enfoque multifacético que integra principalmente conocimientos didácticos —relacionados con estrategias de enseñanza, contextualización y adaptación al estudiantado— y, en menor medida, conocimientos disciplinares vinculados a competencias estadísticas específicas. Este análisis no incluye los ítems relacionados con la dimensión “Prácticas para guiar el aprendizaje de la estadística”, que serán abordados en trabajos futuros. En relación con los conocimientos didácticos, destacan los métodos y estrategias didácticas, haciendo énfasis en la contextualización, y la adaptación a la situación del alumnado. El uso de métodos didácticos variados y una diversidad de estrategias y recursos lúdicos y visuales emerge como un componente crucial para la enseñanza efectiva de la estadística, de acuerdo con Alsina (2020a, 2020b). En especial, se hace hincapié en la contextualización con situaciones reales, ya que no solo facilita la comprensión de conceptos abstractos al hacerlos tangibles y aplicables, sino que también incrementa la motivación y el interés de los estudiantes al demostrar la utilidad práctica de la estadística en su vida diaria (Batanero y Díaz, 2011). Otro dato relevante es el interés del profesorado por ajustarse a las situaciones individuales de los estudiantes, asegurando que todos puedan acceder a los conceptos estadísticos de manera efectiva. Esta adaptabilidad contribuye a un aprendizaje más inclusivo y equitativo (Alsina y Planas, 2008), maximizando el potencial de todos los estudiantes para comprender y aplicar la estadística.

Respecto a los conocimientos disciplinares, el profesorado ha manifestado la necesidad de desarrollar competencias estadísticas específicas, tales como la organización, análisis e interpretación de datos, pues consideran que este conocimiento especializado es esencial para promover que los estudiantes adquieran una comprensión profunda y aplicada de la estadística. Sin embargo, los datos identificados revelan que existe una distancia muy considerable entre los conocimientos que señala el profesorado y las ideas estadísticas fundamentales descritas por Burrill y Biehler (2011) o el conjunto de conocimientos que se incluyen en los currículums (García-Alonso et al., 2025; Vásquez y Alsina, 2023; Vásquez y Cabrera, 2022).

Una limitación de este estudio ha sido el tamaño reducido de la muestra y la sobrerrepresentación de docentes chilenos. Aunque el cuestionario se difundió en diversos países latinoamericanos, la mayoría de las respuestas provienen de Chile, lo que debe considerarse al momento de interpretar los resultados. Además, si bien se dispone de información sobre los años de experiencia docente, no todos los participantes entregaron datos sobre su formación inicial o continua, ni sobre su identidad de género. Estos elementos limitan la posibilidad de realizar un análisis más contextualizado de las trayectorias docentes. No obstante, al tratarse de un estudio exploratorio, el objetivo principal ha sido identificar tendencias iniciales y generar hipótesis que puedan ser profundizadas en investigaciones futuras con muestras más amplias y equilibradas. En este sentido, los resultados aquí presentados constituyen un punto de partida relevante para avanzar en el diseño de planes de desarrollo profesional específicos en educación estadística, atendiendo a las distintas etapas educativas y contextos nacionales.

En conclusión, los resultados obtenidos en este estudio revelan que la formación continua se debería fundamentar en un enfoque integrado que, además de fortalecer los conocimientos estadísticos, debería centrarse en la creación de entornos de aprendizaje que sean relevantes, atractivos y adaptados a los estudiantes. La combinación de contextualización, metodologías didácticas innovadoras, desarrollo de competencias específicas y adaptación pedagógica constituye una estrategia integral que busca no solo la comprensión de la estadística, sino la formación de estudiantes capaces de aplicar estos conocimientos de manera efectiva en su vida diaria y en sus futuros estudios. Desde nuestro punto de vista, este enfoque holístico en la formación continua asegura una enseñanza de la estadística que es a la vez rigurosa y relevante, preparando a los estudiantes para enfrentar y analizar datos en un mundo cada vez más basado en la información.

 

REFERENCIAS BIBLIOGRÁFICAS

 

AA.VV. (2024). Manifiesto a favor de la Alfabetización Estadística. https://www.seio.es/manifiesto-alfabetizacion-estadistica/

Alsina, Á. (2012). La estadística y la probabilidad en Educación Infantil conocimientos disciplinares, didácticos y experienciales. Didácticas Específicas, 7, 4-22.

Alsina, Á. (2020a). Aplicación del enfoque de los itinerarios de enseñanza de las matemáticas a la enseñanza de la estadística en educación primaria. En M.M. Gea. R. Álvarez-Arroyo y J.A. Garzón (Eds.), Seminario Hispano Brasileño de Educación Estadística (pp. 57-60). Grupo PAI FQM-126.

Alsina, Á. (2020b). Enseñar estadística en Educación Primaria: primeras recomendaciones desde el Enfoque de los Itinerarios de Enseñanza de las Matemáticas. En C. Ribeiro y A. Pavan (Eds.), Investigações hispanobrasileiras em Educação Estatística (pp. 107-112). Editora Akademy.

Alsina, Á. y García-Alonso, I. (2023). La estadística y la probabilidad y su didáctica en la formación inicial de maestros en España. Matemáticas, Educación y Sociedad, 6(2), 11-27

Alsina, Á. y Planas, N. (2008). Matemática inclusiva. Propuestas para una educación matemática accesible. Narcea.

Alsina, Á., Vásquez, C., García-Alonso, I. y Berciano, A. (2024). Educación estadística y probabilística para futuros docentes españoles de infantil y primaria: características, enfoque y metodología. Revista Latinoamericana de Investigación en Matemática Educativa 27(1), 73-104. https://doi.org/10.12802/relime.24.2713

Balduino, A.R., Filho, A.D.P., de Sousa Galvão, C., Oliveira, C.S. y Cloux, R.F. (2021). Statistics Education-Teacher Training in Investigative Classes. International Journal of Advanced Engineering Research and Science, 8, 11. https://doi.org/10.22161/ijaers.811.32

Ball, D., Thames, M. y Phelps, G. (2008). Content knowledge for teaching. Journal of Teacher Education, 59(5), 389-407. https://doi.org/10.1177/0022487108324554

Batanero, C. (2004). Los retos de la cultura estadística. Yupana, 1(1), 27-37. https://doi.org/10.14409/yu.v1i1.238

Batanero, C. (2009). Retos para la formación estadística de profesores. En J. A. Fernandes, F. Viseu, H. Martinho y P. Correia (Ed), Actas do II Encontro de Probabilidades e Estatística na Escola (pp. 7-21). Universidade do Minho.

Batanero, C. y Díaz, C. (2011). Estadística con proyectos. Departamento de Didáctica de la Matemática.

Ben-Zvi, D., Gravemeijer, K. y Ainley, J. (2018). Design of statistics learning environments. En D. Ben-Zvi, K. Makar y J. Garfield (Eds.), International Handbook of Research in Statistics Education (pp. 473-502). Springer. https://doi.org/10.1007/978-3-319-66195-7

Ben-Zvi, D. y Garfield, J. (2004). Statistical literacy, reasoning, and thinking: Goals, definitions, and challenges. En D. Ben-Zvi y J. Garfield (Eds.), The challenge of developing statistical literacy, reasoning and thinking (pp. 3-16). Springer. https://doi.org/10.1007/1-4020-2278-6_1

Burgess, T. (2006). A framework for examining teacher knowledge as used in action while teaching statistics. En A. Rossman y B. Chance (Eds.), Working cooperatively in statistics education. Proceedings of the Seventh International Conference on Teaching Statistics (ICOTS7) (pp. 1-6). IASE.

Burgess, T. (2009). Teacher knowledge and statistics: What types of knowledge are used in the primary classroom? The Mathematics Enthusiast, 6(1-2), 3-24.

Burgess, T. (2011). Teacher Knowledge of and for Statistical Investigations. En C. Batanero, G. Burrill y C. Reading (Eds.), Teaching statistics in school mathematics: Challenges for teaching and teacher education. A joint ICMI/IASE study. (pp. 259-270). Springer. https://doi.org/10.1007/978-94-007-1131-0_26

Burgess, T. (2012). How does teacher knowledge in statistics impact on teacher listening? En J. Dindyal, L.P. Cheng y S. Fong (Eds.), Mathematics education: Expanding horizons. Proceedings of the 35th annual conference of the Mathematics Education Research Group of Australasia (pp. 146-153). MERGA.

Burrill, G. y Biehler, R. (2011). Fundamental statistical ideas in the school curriculum and in training teachers. En C. Batanero, G. Burrill y C. Reading (Eds.), Teaching statistics in school mathematics: Challenges for teaching and teacher education (pp. 57-69). Springer. https://doi.org/10.1007/978-94-007-1131-0_10

Callingham, R. y Watson, J.M. (2011). Measuring levels of statistical pedagogical content knowledge. En C. Batanero, G. Burrill y C. Reading (Eds.), Teaching statistics in school mathematics: Challenges for teaching and teacher education. A joint ICMI/IASE study (pp. 283-293). Springer. https://doi.org/10.1007/978-94-007-1131-0_28

Callingham, R., Carmichael, C. y Watson, J.M. (2016). Explaining student achievement: The influence of teachers’ pedagogical content knowledge in statistics. International Journal of Science and Mathematics Education, 14, 1339-1357. https://doi.org/10.1007/s10763-015-9653-2

Carrillo, J., Climent, N., Montes, M., Contreras, L., Flores-Medrano, E., Escudero-Ávila, D., Vasco, D., Rojas, N., Flores, P., Aguilar-González, Á., Ribeiro, M. y Muñoz-Catalán, M.C. (2018). The Mathematics Teacher’s Specialised Knowledge (MTSK) model. Research in Mathematics Education, 20(3), 236-253. https://doi.org/10.1080/14794802.2018.1479981

Cohen, L., Manion, L. y Morrison, L. (2018). Research methods in education (8.ª ed.). Routledge. https://doi.org/10.4324/9781315456539

Comité Español de Matemáticas [CEMat] (2021). Bases para la elaboración de un currículo de Matemáticas en Educación no Universitaria. CEMat. https://hdl.handle.net/10481/101997

Comité Español de Matemáticas [CEMat] (2024). Estudio diagnóstico sobre la situación en competencia matemática. CEMat. https://hdl.handle.net/10481/101995

Estrella, S., Olfos, R. y Mena-Lorca, A. (2015). El conocimiento pedagógico del contenido de estadística en profesores de primaria. Educação e Pesquisa, 41(2), 477-493. https://doi.org/10.1590/S1517-97022015041858

Fernández, M.S., Pomilio, C., Cueto, G., Filloy, J., González-Arzac, A., Lois-Milevicich, J. y Pérez, A. (2020). Improving skills to teach statistics in secondary school through activity-based workshops. Statistics Education Research Journal, 19(1), 106-119. https://doi.org/10.52041/serj.v19i1.124

Franco, J. y Alsina, Á. (2022a). El conocimiento del profesorado de Educación Primaria para enseñar estadística y probabilidad: una revisión sistemática. Aula Abierta, 51(1), 7-16. https://doi.org/10.17811/rifie.51.1.2022.7-16

Franco, J. y Alsina, Á. (2022b). Conocimiento especializado del profesorado de Educación Primaria para enseñar estadística y probabilidad. Educación Matemática, 34(3), 65-96. https://doi.org/10.24844/EM3403.03

Gal, I. (2002). Adults’ Statistical literacy: Meanings, components, responsibilities. International Statistical Review, 70(1), 1-25. https://doi.org/10.1111/j.1751-5823.2002.tb00336.x

Gal, I. (2005). Towards ‘probability literacy’ for all citizens. En G. Jones (Ed.), Exploring probability in school: Challenges for teaching and learning (pp. 43-71). Springer. https://doi.org/10.1007/0-387-24530-8_3

Gal, I. (2012). Developing probability literacy: needs and pressures stemming from frameworks of adult competencies and mathematics curricula. En S. J. Cho (Ed.), Proceedings of the 12th International Congress on Mathematical Education (pp. 1-7). Springer.

García-Alonso, I., Vásquez, C. y Alsina, Á. (2025). Panorama curricular de la alfabetización temprana en estadística y probabilidad. Profesorado, Revista de Currículum y Formación del Profesorado, 29(1), 265-294. https://doi.org/10.30827/profesorado.v29i1.30849X

Garfield, J. y Ben-Zvi, D. (2008a). Developing students’ statistical reasoning. Connecting research and teaching practice. Springer Science & Business Media.

Garfield, J. y Ben-Zvi, D. (2008b). Preparing school teachers to develop students’ statistical reasoning. En C. Batanero, G. Burrill, C. Reading y A. Rossman (Eds.), Proceedings of the ICMI Study 18 and 2008 IASE Round Table Conference (pp. 1-6). ICMI/IASE.

Garfield, J. y Ben-Zvi, D. (2009). Helping students develop statistical reasoning: Implementing a statistical reasoning learning environment. Teaching Statistics, 31(3), 72-77. https://doi.org/10.1111/j.1467-9639.2009.00363.x

Godino, J.D., Batanero, C. y Flores, P. (1999). El análisis didáctico del contenido matemático como recurso en la formación de profesores de matemáticas. En Departamento de Didáctica y Organización Escolar (Ed.), Homenaje al profesor Oscar Sáenz Barrio (pp. 165-185). Universidad de Granada.

Godino, J.D., Batanero, C. y Wilhelmi, M. (2008). Assessing and developing pedagogical content and statistical knowledge of primary school teachers through project work. En C. Batanero, G. Burrill, C. Reading y A. Rossman (Eds.), Proceedings of the ICMI Study 18 and 2008 IASE Round Table Conference (pp. 1-6). ICMI/IASE.

Groth, R. (2007). Toward a conceptualization of statistical knowledge for teaching. Journal for Research in Mathematics Education, 38(5), 427-437. https://doi.org/10.2307/30034960

Groth, R. (2012). The role of writing prompts in a statistical knowledge for teaching course. Teacher Educator, 1(1), 23-40. https://doi.org/10.5951/mathteaceduc.1.1.0023

Groth, R. (2013). Characterizing key developmental understandings and pedagogically powerful ideas within a statistical knowledge for teaching framework. Mathematical Thinking and Learning, 15(2), 121-145. https://doi.org/10.1080/10986065.2013.770718

Koleza, E. y Kontogianni, A. (2012). Statistics in primary education in Greece: How ready are primary teachers? En D. Ben-Zvi y K. Makar (Eds.), The Teaching and Learning of Statistics (pp. 2544-2553). Springer. https://doi.org/10.1007/978-3-319-23470-0_34

Moore, D.S. (1997). New pedagogy and new content: The case of statistics. International Statistical Review, 65(2), 123-137.

Moore, D.S. (1990). Uncertainty. En L.A. Steen (Ed.), On the shoulders of giants: new approaches to numeracy (pp. 95-137). National Academy Press.

Muñiz-Rodríguez, L. y Rodríguez-Muñiz, L.J. (2021). Análisis de la práctica docente en el ámbito de la educación estadística en educación secundaria. Paradigma, 41(e1), 191-220. https://doi.org/10.37618/PARADIGMA.1011-2251.2021.p191-220.id1023

Muñiz-Rodríguez, L., Rodríguez-Muñiz, L.J. y Alsina, Á. (2020). Deficits in the statistical and probabilistic literacy of citizens: Effects in a world in crisis. Mathematics, 8(11), 1872. https://doi.org/10.3390/math8111872

National Committee on Mathematical Requirements [NCMR] (1923). The reorganization of mathematics in secondary education. Mathematical Association of America.

National Council of Teachers of Mathematics [NCTM]. (1989). Curriculum and evaluation standards for school mathematics. NCTM.

National Council of Teachers of Mathematics [NCTM]. (2003). Principios y estándares para la educación matemática. Sociedad Andaluza de Educación Matemática Thales.

Pfannkuch, M. y Ben-Zvi, D. (2011). Developing teachers’ statistical thinking. En C. Batanero, G. Burrill y C. Reading (Eds.), Teaching statistics in school mathematics: Challenges for teaching and teacher education. A joint ICMIIASE study (pp. 323-333). Springer.

Rodríguez-Muñiz, L.J., Muñiz-Rodríguez, L., García-Alonso, I., López-Serentill, P., Vásquez, C. y Alsina, Á. (2022). Navigating between abstraction and context in secondary school statistics education. Culture and Education, 34(3), 689-725. https://doi.org/10.1080/11356405.2022.2058794

Schoen, R. C., LaVenia, M., Chicken, E., Razzouk, R., Kisa, Z. y Boylan, M. (2019). Increasing secondary-level teachers’ knowledge in statistics and probability: Results from a randomized controlled trial of a professional development program. Cogent Education, 6(1), 1613799. https://doi.org/10.1080/2331186X.2019.1613799

Siswono, T.Y.E., Kohar, A.W. y Hartono, S. (2018). Designing tasks to examine mathematical knowledge for teaching statistics for primary teachers. Journal of Physics Conference Series, 947(1), 1-6. https://doi.org/10.1088/1742-6596/947/1/012008

Vásquez, C. y Alsina, Á. (2023). Creencias del profesorado de educación primaria en torno a la enseñanza de la estadística. Revista Chilena de Educación Matemática, 15(3), 90-101. https://doi.org/10.46219/rechiem.v15i3.133

Vásquez, C. y Cabrera, G. (2022). La estadística y la probabilidad en los currículos de matemáticas de educación infantil y primaria de seis países representativos en el campo. Educación Matemática, 34(2), 245-274. https://doi.org/10.24844/EM3402.09

Vásquez, C. Díaz-Levicoy, D., Coronata, C., y Alsina, A. (2018). Alfabetización estadística y probabilística: primeros pasos para su desarrollo desde la Educación Infantil. Cadernos Cenpec, 8(1), 154-179.

Vásquez, C. y Alsina, Á. (2022). La estadística y la probabilidad en los currículos de infantil y primaria: implicaciones para la formación del profesorado. En A. Salcedo y D. Díaz-Levicoy (Eds.), Formación del Profesorado para Enseñar Estadística: Retos y Oportunidades (pp. 189-214). Universidad Católica del Maule.

Vidal-Szabó, P. y Estrella, S. (2020). Extensión del modelo MTSK al dominio estadístico. En Y. Morales-López y Á. Ruíz (Eds.), Educación Matemática en las Américas 2019 (pp. 1036-1042). Comité Interamericano de Educación Matemática.

Vidal-Szabó, P. y Estrella, S. (2023). Conocimiento Especializado de Profesores sobre las Características del Aprendizaje de la Estadística en Educación Básica, bajo la Taxonomía SOLO. Revista de Educación Estadística, 2(1), 1-25. https://doi.org/10.29035/redes.2.1.3

Watson, J.M., Callingham, R. y Donne, J. (2008). Proportional reasoning: Student knowledge and teachers’ Pedagogical Content Knowledge. En M. Goos, R. Brown y K. Makar (Eds.), Navigating currents and charting directions: Proceedings of the 31st Annual Conference of the Mathematics Education Research Group of Australasia (Vol. 1, pp. 563-571). MERGA.

Watson, J.M., Callingham, R. y Donne, J. (2008). Proportional reasoning: Student knowledge and teachers’ Pedagogical Content Knowledge. En M. Goos, R. Brown y K. Makar (Eds.), Navigating currents and charting directions: Proceedings of the 31st Annual Conference of the Mathematics Education Research Group of Australasia (Vol. 1, pp. 563-571). MERGA.

Watson, J.M., Callingham, R. y Nathan, E. (2009). Probing teachers’ Pedagogical Content Knowledge in statistics: «How will Tom get to school tomorrow?». En R. Hunter, B. Bicknell y T. Burgess (Eds.), Crossing divides: Proceedings of the 32nd annual conference of the Mathematics Education Research Group of Australasia (Vol. 2, pp. 563-570). MERGA.

Watson, J.M. (2001). Profiling teachers’ competence and confidence to teach particular mathematics topics: The case of chance and data. Journal of Mathematics Teacher Education, 4, 305-337. https://doi.org/10.1023/A:1013383110860

Wild, C. y Pfannkuch, M. (1999). Statistical thinking in empirical enquiry. International Statistical Review, 67(3), 223-248. https://doi.org/10.1111/j.1751-5823.1999.tb00442.x

Yañez, J. (2016). El conocimiento especializado del profesor de matemática sobre la resolución de problemas de optimización de funciones aplicando el concepto de derivada. Una investigación acción. [Tesis de Doctorado, Pontificia Universidad Católica Valparaíso].

 

Como citar:

Alsina, Á., Vásquez, C., Rodríguez-Muñiz, L.J. y Sánchez, E. (2025). Explorando el desarrollo profesional sobre educación estadística del profesorado en activo. Revista de Educación Estadística, 4, 1-32. https://doi.org/10.29035/redes.4.1.6

 

 

 

 

Esta obra está bajo una licencia de Creative Commons
Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional.

 

 

 

1. 1 *Autor de correspondencia: angel.alsina@udg.edu (Á. Alsina)

   https://orcid.org/0000-0001-8506-1838 (angel.alsina@udg.edu).

2. 2 https://orcid.org/0000-0002-5056-5208 (cavasque@uc.cl).

3. 3 https://orcid.org/0000-0001-8702-8361 (luisj@uniovi.es).

4. 4 https://orcid.org/0000-0002-8995-7962 (esanchez@cinvestav.mx).