|
|
Revista de Educación Estadística Vol. 3, pp. 1-17, ene. 2024 - dic. 2024 ISSN 2810-6164 |
DOI: https://doi.org/10.29035/redes.3.1.3
ALCANCES Y LIMITACIONES CURRICULARES PARA EL DESARROLLO DEL PENSAMIENTO ESTOCÁSTICO EN ESTUDIANTES MEXICANOS DE BACHILLERATO
Âmbitos e limitações curriculares para o raciocínio estatístico de alunos mexicanos do ensino secundário
Curricular scopes and limitations for statistical reasoning of Mexican high school students
Saúl Elizarraras Baena1
Escuela Normal Superior de México (Ciudad de México)
Resumen
El objetivo de esta investigación educativa es analizar el Programa de Estudios sobre Pensamiento matemático 1 que se imparte en el currículo de Bachillerato General en México, en el cual se incluye un solo curso para lo correspondiente a temas de Probabilidad, Estadística descriptiva y Estadística inferencial. Se asume que esta investigación es de tipo cualitativo (Eisner, 1998), cuyo método es el análisis del contenido (Martínez, 2019) y se complementa con la perspectiva de Ojeda (2006). Este curso, de manera inédita, se imparte en primer semestre, cuya razón se debe a que se le considera de manera instrumental como recurso cognitivo para las demás Unidades Académicas Curriculares (UAC) y se encuentra enmarcado en el Marco Curricular Común de la Educación Media Superior (MCCEMS. Si bien es cierto que, en el programa de estudios vigente para bachillerato general (SEP, 2023), se incluye a la Probabilidad y a la Estadística de manera un poco más amplia que en el programa de estudios de 2017 (SEP, 2017); no obstante, se le destinan sólo 64 horas para todo el semestre, por lo que se promete muy difícil que se adquieran los aprendizajes comprometidos. En general, un curso es insuficiente para desarrollar el pensamiento estocástico en estudiantes de bachillerato. Ahora bien, el análisis de algunas de las actividades propuestas en el libro de texto es menester su replanteamiento con la finalidad de que pueda advertirse y comprenderse de manera clara la idea de azar.
Palabras clave: Currículo, Bachillerato, Estudiantes, Pensamiento, Estocástico.
Resumo
O objetivo desta pesquisa educacional é analisar o Programa de Estudos sobre Pensamento Matemático 1 que é ministrado no currículo do Bacharelado Geral no México, que inclui um único curso correspondente aos tópicos de Probabilidade, Estatística Descritiva e Estatística Inferencial. Supõe-se que esta pesquisa seja qualitativa (Eisner, 1998), cujo método é a análise de conteúdo (Martínez, 2019) e é complementada pela perspectiva de Ojeda (2006). Esta unidade curricular, de forma inédita, é ministrada no primeiro semestre, pelo que é considerada instrumentalmente como recurso cognitivo para as restantes Unidades Académicas Curriculares (UAC) e enquadra-se no Quadro Curricular Comum do Ensino Secundário Superior. (MCCEMS. Embora seja verdade que, no atual programa de estudos para o bacharelado geral (SEP, 2023), Probabilidade e Estatística estão incluídas de forma um pouco mais ampla do que no programa de estudos de 2017 (SEP, 2017); no entanto, apenas 64 horas são alocado para todo o semestre, por isso promete-se que será muito difícil adquirir o aprendizado comprometido. Em geral, um curso é insuficiente para desenvolver o pensamento estocástico em alunos do ensino médio. Agora, a análise de algumas das atividades propostas no livro didático exige repensar para que a ideia de acaso possa ser claramente percebida e compreendida.
Palavras-chave: Currículo, Bacharelato, Estudantes, Pensamento, Estocástico
Abstract
The objective of this educational research is to analyze the Study Program on Mathematical Thinking 1 that is taught in the General Baccalaureate curriculum in Mexico, which includes a single course corresponding to topics of Probability, Descriptive Statistics and Inferential Statistics. It is assumed that this research is qualitative (Eisner, 1998), whose method is content analysis (Martínez, 2019) and is complemented by the perspective of Ojeda (2006). This course, in an unprecedented way, is taught in the first semester, the reason for which is that it is considered instrumentally as a cognitive resource for the other Curricular Academic Units (UAC) and is framed in the Common Curricular Framework of Secondary Education Higher (MCCEMS. Although it is true that, in the current study program for general baccalaureate (SEP, 2023), Probability and Statistics are included a little more broadly than in the 2017 study program (SEP, 2017); however, only 64 hours are allocated for the entire semester, so it is promised that it will be very difficult for the committed learning to be acquired. In general, one course is insufficient to develop stochastic thinking in high school students. Now, the analysis of some of the activities proposed in the textbook requires rethinking so that the idea of chance can be clearly noticed and understood.
Keywords: Curriculum, High School, Students, Thinking, Stochastic.
Recibido: 11/12/2023 - Aceptado: 05/04/2024
1. INTRODUCCIÓN
En el presente artículo, se analiza el programa de estudios vigente para el bachillerato general de México (Secretaría de Educación Pública [SEP], 2023a) con la finalidad de valorar sus alcances y limitaciones curriculares para el desarrollo del pensamiento estocástico de estudiantes mexicanos de bachillerato general.
En el marco de la propuesta institucional, se proponen sólo tres cursos denominados como Pensamiento matemático, durante los tres años de bachillerato, los cuales forman parte del currículum fundamental y se conciben como recursos sociocognitivos definidos como aprendizajes articuladores, cuyo papel transversal es lograr los aprendizajes de trayectoria.
Para quien escribe estas líneas, el desarrollo del pensamiento estocástico es un proceso gradual y sistemático, por lo que este curso debería ser ampliado a por lo menos otro semestre y trabajarlo con las cien horas clase semana mes tal y como se consideraban en los programas de estudio anteriores.
Si bien es cierto que con el enfoque actual se debe promover de forma preponderante el humanismo con visión de solidaridad; no obstante, el desarrollo de competencias para el trabajo sigue siendo parte de la formación de los estudiantes de bachillerato. Para lograr este propósito, la comunidad tiene que ser el centro en lugar del individuo, y para ello, se debe desarrollar el pensamiento crítico con fines de transformación social, es decir, identificar y analizar aquellas situaciones o causas que inciden en las desigualdades e injusticias sociales con objeto de que la escuela y la comunidad puedan intervenir en forma conjunta para cambiar las condiciones sociales antes descritas (Diario Oficial de la Federación [DOF], 2019).
En esta investigación, se toman como punto de referencia, algunos estudios que se han llevado a cabo de forma previa, los cuales refieren a la comprensión de ideas fundamentales de estocásticos de estudiantes de quinto semestre de bachillerato general (Elizarraras, 2021); también se reconocen las aportaciones que se han dado a conocer en investigaciones que plantean innovaciones curriculares mediante la relación entre física moderna y la probabilidad en el bachillerato del Instituto Politécnico Nacional (Ávila y Suárez, 2021) o incluso, de la interpretación de una situación binomial por estudiantes de bachillerato, desde un acercamiento a la comprensión del enfoque frecuencial, al realizar el lanzamiento a una canasta de baloncesto (Begué et al., 2021).
Estos estudios dan la pauta para mostrar interés en el análisis del programa sintético que se plantea para bachillerato general y de un libro de texto que se utilizan como medios para el desarrollo del pensamiento estocástico, por lo que aquí se plantea la pregunta de investigación: ¿cuáles son los alcances y limitaciones curriculares para el desarrollo del pensamiento estocástico en estudiantes de primer semestre de bachillerato general cuando se utiliza como medio el programa de estudios?
2. PERSPECTIVA TEÓRICA
Se presentan aspectos epistemológicos, sociales y cognitivos que devienen en criterios de análisis.
2.1. Aspectos epistemológicos
Desde una perspectiva epistemológica, Heitele (1975) enuncia diez ideas fundamentales de estocásticos que pueden ayudar a construir un currículo coherente para temas de Estadística y Probabilidad.
1) Medida de probabilidad. Consiste en normar nuestras creencias, a los eventos imposibles se les asigna la probabilidad de cero y a los eventos seguros la probabilidad de uno; todos los eventos posibles de un fenómeno aleatorio se encuentran comprendidos en el intervalo cerrado [0, 1].
2) Espacio muestra. También conocido como espacio muestra, compuesto por todos y cada uno de los eventos que pertenecen a un fenómeno aleatorio.
3) Regla de la adición. Consiste en obtener nuevas probabilidades a partir de las iniciales, es decir, estimar la probabilidad de eventos compuestos a partir de eventos elementales.
4) Independencia. Se le expresa por la regla del producto y comúnmente se le hace referencia cuando la ocurrencia de un evento no afecta la ocurrencia de otro.
5) Equidistribución y simetría. También se le puede conocer como equiprobabilidad cuando ninguno de los eventos se privilegia sobre los otros y de forma interrelacionada, la simetría emerge cuando la equidistribución no es evidente desde el principio.
6) Combinatoria. Se le concibe más allá de ser un auxiliar para la probabilidad, ya que más que ser simplemente algoritmos estándar para calcular campos de probabilidad de experimentos aleatorios complejos, suministran una entrada sencilla, en particular en su forma icónica y activa.
7) Modelo de urna y simulación. Su importancia radica en el hecho de que permite estimular procesos aleatorios complejos mediante una sucesión de urnas que modelan fenómenos aleatorios que por su naturaleza podrían ser muy difícil de estudiar en condiciones reales.
8) Variable aleatoria. Es una función cuyo espacio muestra asigna valores numéricos correspondientes a un fenómeno aleatorio, según la equidistribución.
9) Ley de los grandes números. De manera general, se le plantea como a mayor número de repeticiones de un fenómeno aleatorio, mayor aproximación a la probabilidad de los eventos que lo conforman. Más importante aún es precisar que esta idea está en la base de todas las aplicaciones de probabilidad.
10) Muestra. Su importancia es que nuestros conocimientos y juicios se basan en partes de una población.
Estas ideas se conciben en una espiral curricular que tiene como punto de partida un plano intuitivo, el cual avanza hacia un plano formal, por lo que no tienen un carácter estructural. El autor enfatiza que pueden ser utilizadas para elaborar currículo coherente de estocásticos.
2.2. Aspectos sociales
Para Steinbring (2005), el aprendizaje de los estudiantes es un objetivo a largo plazo, toda vez que la práctica de la enseñanza y el aprendizaje de las matemáticas se caracterizan por una gran variedad de construcciones e interpretaciones matemáticas. Para ello, propone el triángulo epistemológico en el que se encuentran interrelacionados el objeto, el concepto y el signo. El primero, es producto de la actividad intelectual, el segundo es la definición de la cosa y el tercero es la representación abstracta en la cual se encuentra interrelacionado el significado y el significante.
2.3. Aspectos cognitivos
Fischbein (1975) enfatiza que la enseñanza puede contribuir en la adquisición temprana de intuiciones correctas sobre estocásticos, lo cual es sumamente importante debido a que a mayor edad se vuelven más difíciles de erradicar. El autor define a las intuiciones como adquisiciones cognitivas que intervienen directamente en las acciones prácticas o mentales, en virtud de sus características globales, inmediatas, estructurales, extrapolatorias y autoevidentes.
Frawley (1999) enfatiza que nada es completamente social ni totalmente individual, ya que la mente social y la mente computacional confluyen simultáneamente mediante la interacción que se da entre sus pares quienes ponen en juego el lenguaje y el pensamiento en un contexto específico; por lo tanto, considera al ser humano tanto máquina como persona; de esta manera, el autor caracteriza tres tipos de subjetividad: el procesamiento no consciente, la conciencia y la metaconciencia.
3. MÉTODO
Esta investigación educativa tiene carácter cualitativo desde la perspectiva de Eisner (1998); en particular, el autor pone especial atención en la crítica educativa cuya finalidad es la mejora del proceso educativo. Así, Eisner (1998) puntualiza que la crítica educativa no sólo debe dirigirse a quienes se encargan de la enseñanza, sino también a los administradores de las escuelas y a los responsables de la política educativa.
En concordancia con Eisner (1998), el crítico educativo debe tener experiencia en la enseñanza para que sus opiniones se basen en conocimientos y experiencias; mientras que si se trata de las personas que administran las escuelas, se espera que estén visitando las aulas de forma constante con objeto de brindar acompañamiento pedagógico y sensibilizarse de los apoyos que debe otorgar para que se alcancen los propósitos de estudio y en lo que corresponde a los responsables de la política educativa se espera que tomen mejores decisiones y lleven a cabo acciones basadas en el funcionamiento de las escuelas.
Complementariamente, Eisner (1998) plantea que la validez de nuestros juicios e interpretaciones dependen de la corroboración estructural, la validez consensual y la adecuación referencial. Con la primera característica, se considera que la credibilidad y confianza de las observaciones o interpretaciones, dependen la confluencia de evidencias. En cuanto a la segunda característica, implica un acuerdo entre diversas personas competentes de que son correctas la descripción, la interpretación, evaluación y temática de una situación educativa. Respecto a la tercera característica, se destaca que la percepción e interpretación de las cualidades correspondientes al proceso educativo cuyo propósito es aumentar la comprensión humana a través de la crítica educativa.
Ahora bien, Ojeda (2006) señala que cuando se conjuga docencia e investigación en lo que denomina aula normal, se presenta una estrecha relación con los modos y los medios que el investigador utiliza para guiar la enseñanza del tema de estudio. En este sentido, ha propuesto un órgano operativo de la investigación en estocásticos, en el cual considera los criterios siguientes: ideas fundamentales de estocásticos, otros conceptos matemáticos implicados, registros semióticos de la información y términos que orientan el pensamiento de lo posible, es decir, aquellos vocablos que por su naturaleza aluden a la idea de azar, por ejemplo, probable, posible, incertidumbre, etcétera; los cuales permiten la identificación y el análisis de aquellos términos que hacen referencia a aspectos de corte determinista.
4. ANÁLISIS E INTERPRETACIÓN DE RESULTADOS
En este apartado, se presenta el análisis del Programa sintético de Pensamiento matemático 1, incluyendo los aspectos que se le relacionan en el Acuerdo número 09/08/23. Posteriormente, a modo de ejemplo, una propuesta una propuesta de trabajo que se plantea en un libro de texto (Ferrusca y Mondragón, 2023).
4.1. Análisis del Programa sintético de Pensamiento matemático 1 (Estocásticos)
En los segundo y tercer párrafos del Artículo 9 del ACUERDO número 09/08/23 por el que se establece y regula el Marco Curricular Común de la Educación Media Superior, se precisa la función y los alcances de los recursos sociocognitivos, a saber:
La función de los recursos sociocognitivos en el proceso de aprendizaje es ampliar, potenciar y consolidar el Conocimiento de la experiencia; permiten aprovechar y aplicar los conocimientos de las Áreas de conocimiento (ciencias naturales, experimentales y tecnología, ciencias sociales y humanidades).
Asimismo, los recursos sociocognitivos contribuyen a desarrollar capacidades, destrezas, habilidades, actitudes y Valores en las y los estudiantes, brindando la posibilidad de construir la propia experiencia, para que sepan qué hacer con el Conocimiento que tienen, sepan actuar, entendiendo lo que hacen, comprendiendo cómo participar y colaborar, asumiendo la responsabilidad de las acciones realizadas, sus implicaciones y consecuencias, y transformando los contextos locales y comunitarios en pro del bien común. (SEP, 2023b; p. 9).
En la Figura 1, se muestra la organización educativa del Marco Curricular Común de la Educación Media Superior (MCCEMS). Como se puede identificar, se divide en tres tipos de currículum: fundamental, laboral y ampliado. En el primer caso, se clasifican en recursos sociocognitivos y Áreas de conocimiento; en el segundo, se consideran las competencias laborales (básicas y extendidas) y en el tercero, se incluyen los recursos socioemocionales y los ámbitos de la formación socioemocional.
De manera específica, en el artículo 11 del Acuerdo número 09/08/23 se define al pensamiento matemático como un recurso sociocognitivo y se indica todo lo que involucra (sic):
Artículo 11. Pensamiento matemático es un recurso sociocognitivo que involucra diversas actividades desde la ejecución de operaciones y el desarrollo de procedimientos y algoritmos hasta los procesos mentales abstractos que se dan cuando el sujeto participa del quehacer matemático, al resolver problemas, usar o crear modelos, y le dan la posibilidad de elaborar tanto conjeturas como argumentos; organizar, sustentar y comunicar sus ideas.
El recurso sociocognitivo de Pensamiento matemático se integra de las siguientes Categorías: Procedural, Procesos de razonamiento, Solución de problemas y modelación, e Interacción y lenguaje algebraico. (SEP, 2023b; p. 9)}
De las cuatro categorías que se consideran para el desarrollo del pensamiento matemático, sólo en dos se puede identificar alguna relación con lo correspondiente a la Probabilidad y la Estadística, en la primera categoría con la subcategoría de Manejo de Datos e Incertidumbre se incluyen temáticas como la enumeración, elementos descriptivos y cálculo combinatorio; mientras que, en la segunda categoría, con el Pensamiento aleatorio, los sistemas de datos, tratamiento de incertidumbre y azar.
Otro concepto que es importante de incluir como parte de este análisis es el de progresiones, ya que cada uno de los tres programas que corresponden al desarrollo del Pensamiento matemático se encuentran organizadas bajo esta idea. En la fracción XXVI del artículo 3 del Acuerdo 09/08/23 se establece la definición que oficialmente se ha emitido al respecto, a saber: “A la descripción secuencial de aprendizajes de conceptos, Categorías y Subcategorías y relaciones entre ellos, que llevarán a los estudiantes a desarrollar conocimientos y habilidades de forma gradual.” (SEP, 2023b, p. 6)
Si bien es cierto que institucionalmente se considera que las progresiones son un modelo flexible que ofrece libertad al docente para adaptar estrategias de acuerdo con el contexto respectivo (SEP, 2023b), también es importante precisar que no es trivial ni inmediato el hecho de que se pretenda el desarrollo de relaciones (de lo más simple a lo más complejo) construidas desde la inter y multidisciplinar y, cuando sea posible la transversalidad mediante la integración de categorías y conceptos.
Figura 1
Organización Educativa del Marco Curricular de la Educación Media Superior.
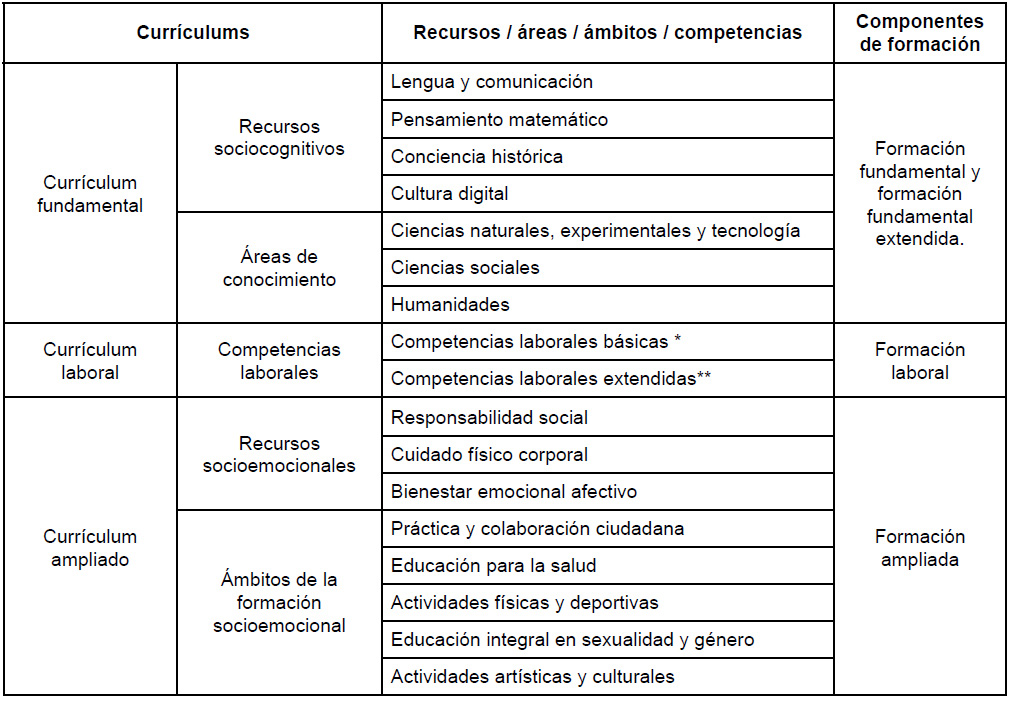
Fuente: SEP (2023b, p. 8).
De modo específico, el programa de Estudios para el curso de Pensamiento matemático 1, se compone de quince progresiones, las cuales se enuncian e interpretan en términos del órgano operativo para la investigación en estocásticos (Ojeda, 2006). En cada progresión, se especifican algunas de las cuatro categorías que se proponen en el programa de estudios y las correspondientes metas de aprendizaje (CnMn), en este sentido, se reconocen cuatro categorías, a saber: procedural, procesos de razonamiento, solución de problemas y modelación e interacción y lenguaje matemático. De estas categorías se desprenden las metas de aprendizaje correspondientes.
En la primera progresión no se identificaron ideas fundamentales de estocásticos, tampoco otros conceptos matemáticos ni la especificación de algún registro semiótico de la información, sólo términos que orientan el pensamiento de lo posible, tales como: decisiones, recolección, organización y datos.
1. Discute la importancia de la toma razonada de decisiones, tanto a nivel personal como colectivo, utilizando ejemplos reales o ficticios que sean significativos para las y los estudiantes y en los que se valore la recolección y organización de datos (C2M1).
En la segunda progresión se identificaron las siguientes ideas fundamentales de estocásticos: medida de la probabilidad, espacio muestra, modelo de urna y simulación, variable aleatoria, muestra y ley de los grandes números. Por otra parte, no se identificaron otros conceptos matemáticos ni la especificación de algún registro semiótico, sólo términos que orientan el pensamiento de lo posible, tales como: incertidumbre, variabilidad, datos, simulaciones, frecuencia, evento, ocurrir, probabilidad y suceda.
2. Identifica la incertidumbre como consecuencia de la variabilidad y a través de la consulta de datos o simulaciones, considera la frecuencia con la que un evento puede ocurrir con la finalidad de tener más información sobre la probabilidad de que dicho evento suceda (C2M1, C2M2).
En la tercera progresión se identificaron las siguientes ideas fundamentales de estocásticos: equidistribución y simetría, modelo de urna y simulación, muestra, ley de los grandes números; respecto a otros conceptos matemáticos sólo se hace alusión al de número; no se alude a algún registro semiótico de la información y se enuncian términos que orientan el pensamiento de lo posible, tales como: equiprobabilidad, repeticiones, simulación, frecuencia, evento y probabilidad teórica.
3. Identifica la equiprobabilidad como una hipótesis que, en caso de que se pueda asumir, facilita el estudio de la probabilidad y observa que cuando se incrementa el número de repeticiones de una simulación, la frecuencia del evento estudiado tiende a su probabilidad teórica (C1M1, C3M1, C4M1).
En la cuarta progresión se reconocieron las ideas fundamentales de estocásticos siguientes: medida de la probabilidad, espacio muestra, regla de la adición, regla del producto e independencia y combinatoria; con relación a otros conceptos matemáticos también se específica el caso de número y se descarta algún registro semiótico de la información, sólo términos que orientan el pensamiento de lo posible, tales como: conteo, combinaciones, ordenaciones, repetición, casos posibles, favorables y eventos.
4. Elige una técnica de conteo (listados, diagramas de árbol, combinaciones, ordenaciones con repetición, ordenaciones sin repetición, etc.) para calcular el número total de casos posibles y casos favorables para eventos simples con la finalidad de hallar su probabilidad y con ello generar una mayor conciencia en la toma de decisiones (C1M2, C1M3, C2M3)
En la quinta progresión se identificaron las ideas fundamentales de estocásticos: medida de la probabilidad, regla de la adición y la regla del producto e independencia. No se incluyen otros conceptos matemáticos ni algún registro semiótico de la información, sólo términos que orientan el pensamiento de lo posible, tales como: Probabilidad, evento, excluyentes, independientes y condicionales.
5. Observa cómo la probabilidad de un evento puede actualizarse cuando se obtiene más información al respecto y considera eventos excluyentes e independientes para emplearlos en la determinación de probabilidades condicionales. (C2M4)
En la sexta progresión, sólo se identificaron ideas fundamentales de estocásticos como: muestra y variable aleatoria, no se identificaron otros conceptos matemáticos ni la especificación de algún registro semiótico de la información, sólo términos que orientan el pensamiento de lo posible, tales como: recolectar, información, datos y variables.
6. Selecciona una problemática o situación de interés, con la finalidad de recolectar información y datos de fuentes confiables e identifica las variables relevantes para su estudio. (C1M1, C4M2)
En la séptima progresión no se identificaron ideas fundamentales de estocásticos, tampoco otros conceptos matemáticos, sólo registros semióticos de la información, tales como: gráficas de barras, gráficos de puntos e histogramas; mientras que respecto a términos que orientan el pensamiento de lo posible, sólo el de datos.
7. Analiza datos categóricos y cuantitativos de alguna problemática o situación de interés para el estudiantado, a través de algunas de sus representaciones gráficas más sencillas como las gráficas de barras (variables cualitativas) o gráficos de puntos e histogramas (variables cuantitativas). (C2M2)
En la octava progresión sólo se incluye la idea de independencia como parte de las ideas fundamentales de estocásticos, no hubo otros conceptos matemáticos ni algún registro semiótico de la información, sólo términos que orientan el pensamiento de lo posible, tales como: variables e independientes.
8. Analiza cómo se relacionan entre sí dos o más variables categóricas a través del estudio de alguna problemática o fenómeno de interés para el estudiantado, con la finalidad de identificar si dichas variables son independientes. (C2M3)
En la novena progresión no hubo ideas fundamentales de estocásticos ni otros conceptos matemáticos, tampoco algún registro semiótico de la información, sólo términos que orientan el pensamiento de lo posible, tales como: correlación y variables.
9. Analiza dos o más variables cuantitativas a través del estudio de alguna problemática o fenómenos de interés para el estudiantado, con la finalidad de identificar si existe correlación entre dichas variables. (C1M3, C2M4)
En la décima progresión no hubo ideas fundamentales de estocásticos ni otros conceptos matemáticos, tampoco algún registro semiótico de la información, sólo términos que orientan el pensamiento de lo posible, tales como: estadísticas y variables.
10. Cuestiona afirmaciones estadísticas y gráficas, considerando valores atípicos (en el caso de variables cuantitativas) y la posibilidad de que existan factores o variables de confusión. (C4M2)
En la onceava progresión sólo se identifica una idea fundamental de estocásticos: muestra, no hubo otros conceptos matemáticos ni algún registro semiótico de la información, sólo términos que orientan el pensamiento de lo posible, tales como: imposibilidad, población, muestreo, aleatoriedad y muestra.
11. Identifica, ante la imposibilidad de estudiar la totalidad de una población, la opción de extraer información de ésta a través del empleo de técnicas de muestreo, en particular, valora la importancia de la aleatoriedad al momento de tomar una muestra. (C3M3)
En la doceava progresión no se identificaron ideas fundamentales de estocásticos ni otros conceptos matemáticos, tampoco la especificación de algún registro semiótico de la información, sólo términos que orientan el pensamiento de lo posible, tales como: observaciones y experimentos.
12. Valora las ventajas y limitaciones de los estudios observacionales y los compara con el diseño de experimentos, a través de la revisión de algunos ejemplos tomados de diversas fuentes. (C4M1)
En la treceava progresión no se identificaron ideas fundamentales de estocásticos ni otros conceptos matemáticos, tampoco algún registro semiótico de la información, sólo términos que orientan el pensamiento de lo posible, tales como: medidas de tendencia central (moda, mediana y media) y medidas de dispersión (desviación estándar, varianza, rango intercuartil, etc.).
13. Describe un fenómeno, problemática o situación de interés para el estudiantado utilizando las medidas de tendencia central (media, mediana y moda) y de dispersión (desviación estándar, varianza, rango intercuartil, etc.) adecuadas al contexto y valora que tipo de conclusiones puede extraer a partir de dicha información. (C2M4, C3M3)
En la catorceava progresión se identificaron las siguientes ideas fundamentales de estocásticos: medida de probabilidad, espacio muestra, variable aleatoria, muestra y ley de los grandes números; no hubo otros conceptos matemáticos ni algún registro semiótico de la información, sólo términos que orientan el pensamiento de lo posible: evento, aleatorio, distribución, normal, probabilidad, evento y suceda.
14. Explica un evento aleatorio cuyo comportamiento puede describirse a través del estudio de la distribución normal y calcula la probabilidad de que dicho evento suceda. (C3M3, C4M3)
En la quinceava progresión se identificaron las siguientes ideas fundamentales de estocásticos: variable aleatoria, muestra y ley de los grandes números; no hubo otros conceptos matemáticos ni la especificación de algún registro semiótico de la información, sólo términos que orientan el pensamiento de lo posible, tales como: posibilidad, inferencias, estadística inferencial y modelarse.
15. Valora la posibilidad de hacer inferencias a partir de la revisión de algunas propiedades de la distribución normal y del sentido de la estadística inferencial para considerar algunos fenómenos que pueden modelarse con dicha distribución. (C2M4, C3M4, C1M3)
Si bien es cierto que las diez ideas fundamentales se incluyen de manera general en las quince progresiones, se debe hacer hincapié en que no se les identifica de forma interrelacionada en cada progresión. Respecto a los otros conceptos matemáticos son excluidos; mientras que los registros semióticos propuestos son escasos y no se les otorga la importancia que tienen para que se pueda utilizar de manera estratégica en la comprensión de la idea de azar.
Ahora bien, estas quince progresiones deben dosificarse en tres evaluaciones parciales durante el semestre, por lo que se espera que, en cada una, se desarrollen cinco progresiones, aproximadamente, una por semana (cuatro horas clase semana mes, 64 horas en todo el semestre).
4.2. Propuesta de trabajo para la Progresión de Aprendizaje 2 en un libro de texto
En el libro de texto de Ferrusca y Mondragón (2023) se plantea una propuesta para la segunda progresión de aprendizaje, en la cual se consideran como contenidos principales los siguientes: Diagramas de Venn, Eventos aleatorios y Cálculo de la probabilidad frecuencial.
En cuanto al primer contenido, se inicia con la definición de Diagrama de Venn y se propone la resolución de un problema contenido en una única situación relacionada con clases de regularización de Inglés y Matemáticas que son ofrecidas por una maestra. La situación planteada es la siguiente:
“La maestra Pula está ofreciendo clases de regularización de Inglés y Matemáticas en línea y por las tardes, en un horario de 5:00 a 6:00 y de 6:00 a 7:00. Fueron 10 los estudiantes interesados que se registraron, pero sólo cinco se conectaron a dichas clases: dos de ellos toman las dos asignaturas, tres asisten a la clase de Ingles y cuatro a la de Matemáticas.” (p. 26).
Posteriormente, se representa el diagrama de Venn y se formulan algunas preguntas reflexivas. Si bien es cierto que se propone un Código QR para la construcción de un Diagrama de Venn, también es importante señalar que se encuentra al final de la hoja y no se le vincula de forma directa con la actividad.
En la Figura 2, se muestran las preguntas reflexivas y el diagrama de Venn completado incorrectamente, ya que si cada estrella representa a un estudiante no se corresponden con los diez estudiantes referidos.
Figura 2
Diagrama de Venn y preguntas reflexivas sobre la situación planteada.
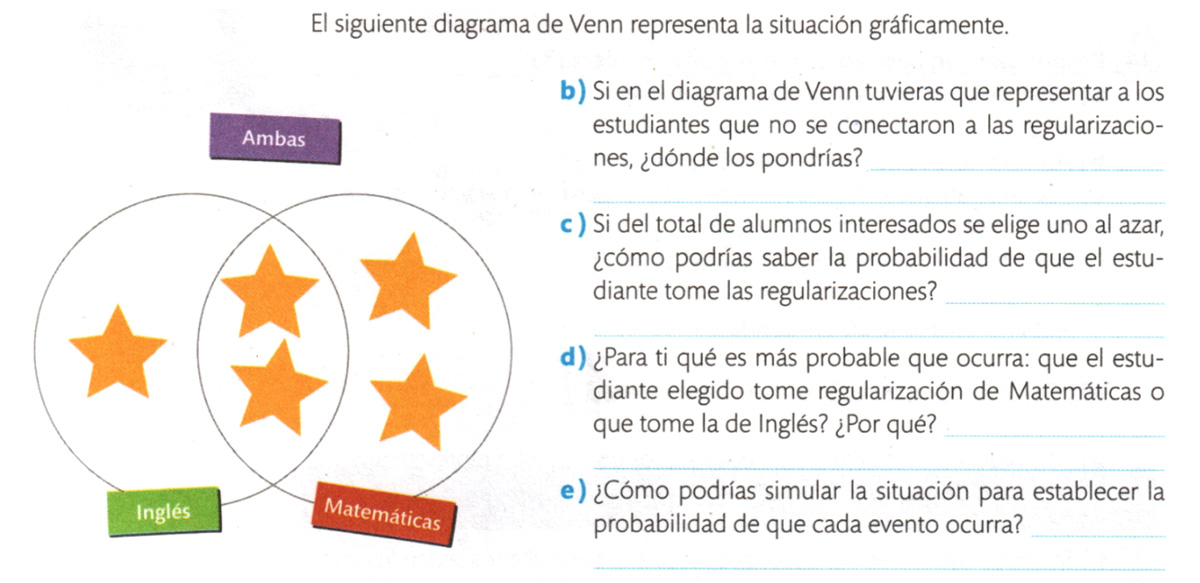
Fuente: Imagen recuperada del libro de texto de Ferrusca y Mondragón (2023, p. 26).
El segundo tema (eventos aleatorios) también inicia con la definición del concepto que ya en sí mismo es redundante porque el sólo término de eventos incluye lo aleatorio. A continuación, se cita lo presentado en el libro: “Un evento aleatorio es acontecimiento de un hecho en proceso o que está por venir. Se dice que es aleatorio porque no es posible determinar con exactitud qué sucederá.” (p. 27).
Enseguida, la situación que se propone hace referencia al lanzamiento de un dado con figuras geométricas en lugar de números o puntos y se plantea la hipotética obtención de los resultados luego de lanzarlo diez veces; en un segundo momento, se plantea hipotéticamente que se obtuvieron resultados al lanzar doscientas veces el dado y se presentan en una tabla, lo único que debe hacerse es el cálculo de la frecuencia relativa y contestar una pregunta reflexiva. En la Figura 3, se muestra la situación en forma completa.
Figura 3
Situación hipotética planteada para los resultados obtenidos al lanzar 200 veces el dado.

Fuente: Imagen recuperada del libro de texto de Ferrusca y Mondragón (2023, p. 28).
A modo de complemento, se pide que se reflexione cuando un evento tiene mayor o menor probabilidad a partir de la misma situación del lanzamiento de un dado y al final, se solicita la realización del lanzamiento del dado en trescientas ocasiones. Este orden de las actividades y el número de veces que se debe lanzar el dado, pueden ser insuficientes para comprender el enfoque frecuencial como un acercamiento natural a la comprensión de la idea de azar (Gigerenzer y Hoffrage, 995); por el contrario, se debería proponer en primer lugar, el lanzamiento de un número suficiente de veces el dado y ya después, situaciones como la mostrada en la figura 3.
Otro aspecto que debe destacarse con el uso de este libro de texto es que la probabilidad se le define como un campo de las matemáticas que estudia sucesos o fenómenos e incluso, experimentos aleatorios. Es evidente que el uso de estos términos es indistinto y que debe haber mayor claridad para coadyuvar en la advertencia de la idea de azar y con ello, en el desarrollo del pensamiento estocástico. Además, se utiliza de forma inapropiada el término experimento, ya que hace evoca situaciones de tipo determinista en las cuales los posibles resultados se pueden conocer con certeza. Tampoco se explica de forma clara la idea de que, a mayor número de repeticiones de un fenómeno aleatorio, mayor aproximación a la probabilidad de ocurrencia de cada uno de los eventos que lo conforman:
Entre más veces se lleva a cabo un experimento aleatorio, más regulares son los resultados; por ejemplo, cuántas más veces se lance un dado, más veces saldrá cada número y la cantidad de ocasiones en las que esto ocurra será más parecida. (Ferrusco y Mondragón, 2023; p. 29).
Con referencia al tercer contenido (Cálculo de la probabilidad frecuencial), la propuesta de trabajo es la misma, primero situaciones hipotéticas y de forma seguida, se debe realizar cincuenta veces el lanzamiento de dos dados ordinarios numerados del uno al seis. En la figura 4, se muestra la introducción del contenido con un ejemplo que hacen referencia a la frecuencia relativa, expresada de forma exclusiva e incorrecta en porcentaje y excluyendo su representación en forma decimal.
Figura 4
Introducción y situación propuesta para trabajar el contenido de Cálculo de la probabilidad frecuencial.

Fuente: Imagen recuperada del libro de texto de Ferrusca y Mondragón (2023, p. 29).
Aunado a lo antes expuesto, la frecuencia relativa no es propiamente la probabilidad frecuencial. Aquí se hace referencia al enfoque frecuencial de la probabilidad porque es una manera suigéneris para estimar la probabilidad de un evento correspondientea un fenómeno aleatorio en particular.
Si bien es cierto que este tema se complementa con otras actividades que hacen uso de la tecnología mediante el acceso a otro código QR y mediante el uso de GeoGebra, el número de repeticiones debería ser mayor para que se pueda tener más claridad en el acercamiento a la comprensión de las ideas fundamentales de estocásticos de muestra y ley de los grandes números. Además, no se omite señalar que no todos los estudiantes mexicanos tienen acceso a celular e internet; incluso, ni el profesorado tiene acceso ni domino pleno con el uso de la tecnología, por lo que, a la fecha, se reconocen retos múltiples, pero muy complicados por la infraestructura tan diversa que hay en las escuelas.
5. A MODO DE CONCLUSIONES
Uno de los alcances del programa de estudios de Pensamiento matemático I es que se incluyen todas las ideas fundamentales de estocásticos, aunque no de forma interrelacionada ni sistemática, ya que sus propósitos son muy ambiciosos para tan poco tiempo que se le destina al semestre (64 horas en total). Respecto a otros conceptos matemáticos sólo hace explícito el de número y en el caso de registros semióticos de la información, se incluyen gráficas y diagramas de árbol, pero se excluye a la lengua natural y el uso explícito de tablas. Con referencia a los términos que orientan el pensamiento de lo posible se pudieron identificar diversos, solo es cuestionable el de experimento de la progresión número doce porque evoca a situaciones de tipo determinista.
Una limitación es que se pudo identificar que las quince progresiones incluyen temas relacionados con tres cursos, a saber: Probabilidad, Estadística descriptiva y Estadística inferencial. En este sentido, el tiempo resulta insuficiente para lograr un estudio reflexivo y a profundidad de estos tópicos.
Aunado a lo anterior, la comprensión de ideas fundamentales requiere de tiempo, por lo que se promete difícil lograr el propósito central que es reconocer la incertidumbre para actuar en un mundo complejo y globalizado, caracterizado por la presencia de fenómenos aleatorios y deterministas.
Con relación al libro de texto analizado, es sumamente importante que sea revisado minuciosamente por especialistas en el área con la finalidad de que se puedan proponer actividades de manera adecuada y hacer uso de conceptos en forma apropiada, con la finalidad de que pueda favorecer de manera amplia los aprendizajes de la población estudiantil.
Derivado de lo anterior, la formación docente sigue siendo un asunto pendiente en la agenda de las políticas públicas en educación matemática, así como una necesidad imperante para que el magisterio que se dedica a la enseñanza de las Matemáticas pueda discernir respecto a la pertinencia del uso del libro de texto como apoyo para el proceso de enseñanza y del de aprendizaje.
REFERENCIAS BIBLIOGRÁFICAS
Ávila, G. y Suárez, L. (2021). Una innovación curricular de la relación entre Física moderna y la Probabilidad en el bachillerato del Instituto Politécnico Nacional. En J.D. Zacarías (Ed.), Innovación en los Procesos de Enseñanza y Aprendizaje de lo Estadístico y lo Estocástico (pp. 1-18). Benemérita Universidad Autónoma de Puebla.
Begué, N., Díaz-Levicoy, D., Batanero, C. y Gea, M.M. (2021). Lanzamiento a una canasta de baloncesto: interpretación de una situación binomial por estudiantes de Bachillerato. En J.D. Zacarías (Ed.), Innovación en los Procesos de Enseñanza y Aprendizaje de lo Estadístico y lo Estocástico (pp. 19-35). Benemérita Universidad Autónoma de Puebla.
DOF (2019). Ley General de Educación. Cámara de Diputados.
Eisner, E. (1998). El ojo ilustrado. Indagación cualitativa y mejora de la práctica educativa. Paidós.
Elizarraras, S. (2021). Enseñanza y comprensión sobre ideas fundamentales de estocásticos en bachillerato: Condiciones iniciales. En J.D. Zacarías (Ed.), Innovación en los Procesos de Enseñanza y Aprendizaje de lo Estadístico y lo Estocástico (pp. 77-99). Benemérita Universidad Autónoma de Puebla
Ferrusca, A. y Mondragón, A. (2023). Pensamiento Matemático 1. Bachillerato. Esfinge.
Fischbein, E. (1975). The intuitive Sources of Probabilistic Thinking. Reidel.
Frawley, W. (1999). Vygotsky y la ciencia cognitiva. Paidós.
Gigerenzer, G. y Hoffrage, U. (1995). How to Improve Bayesian Reasoning Without Instruction. Frequency Formats. Psychological Review, 102, 684-704.
Heitele, D. (1975). An epistemological View on Fundamental Stochastic Ideas. Educational Studies in Mathematics, 6, 187-205.
Martínez, F. (2019). El nuevo oficio del investigador educativo. Una introducción metodológica. Universidad Autónoma de Aguascalientes.
Ojeda, A.M. (2006). Estrategia para un perfil nuevo de docencia: un ensayo en la enseñanza de estocásticos. En E Filloy (Ed.), Matemática Educativa, treinta años: una mirada fugaz, una mirada externa y comprensiva, una mirada actual (pp. 195-214). Santillana y Centro de Investigación y de Estudios Avanzados.
SEP (2017). Programa de estudios. Matemáticas I. Primer semestre. Dirección General de Bachillerato de la Secretaría de Educación Pública.
SEP (2023a). Progresiones de aprendizaje del recurso sociocognitivo Pensamiento matemático. Secretaría de Educación Pública.
SEP (2023b). ACUERDO número 09/08/23 por el que se establece y regula el Marco Curricular Común de la Educación Media Superior. Diario Oficial de la Federación.
Steinbring, H. (2005). The Construction of New Mathematical Knowledge in Classroom Interaction. An Epistemological Perspective. Springer.
Como citar:
Elizarraras, S. (2024). Alcances y limitaciones curriculares para el desarrollo del pensamiento estocástico en estudiantes mexicanos de bachillerato. Revista de Educación Estadística, 3, 1-17. https://doi.org/10.29035/redes.3.1.3

Esta obra está bajo una licencia de Creative Commons
Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional.
1*Autor de correspondencia: sauleliba@gmail.com (S. Elizarraras)
http://orcid.org/0000-0002-9623-3452 (sauleliba@gmail.com).
