|
|
Revista de Educación Estadística Vol. 3, pp. 1-20, ene. 2024 - dic. 2024 ISSN 2810-6164 |
DOI: https://doi.org/10.29035/redes.3.1.4
O BRINCAR E O LETRAMENTO ESTATÍSTICO: UM POSSÍVEL CENÁRIO PARA INVESTIGAÇÃO?
Juego y Alfabetización Estadística: ¿un posible escenario de investigación?
Games and Statistical Literacy: a possible Landscapes of Investigation?
Pedro Henrique Barcarolo1
Universidade de São Paulo (São Paulo, Brasil)
Raquel Milani2
Universidade de São Paulo (São Paulo, Brasil)
Resumo
Este texto apresenta uma investigação, a qual objetivou analisar as potencialidades de brincadeiras promoverem o Letramento Estatístico. Para tal, aponta referenciais teóricos acerca de Brincadeiras e Letramento Estatístico relacionado cenários para investigação. A partir de tais marcos, esta pesquisa tem um caráter qualitativo e transcorre sob o delineamento de pesquisa-ação. O corpus é composto pelo relato de experiência considerando a observação participante e notas de campo do professor-pesquisador, considerando os momentos de grupos de discussão e o desenvolvimento da atividade. A pesquisa foi aplicada em uma escola municipal de São Paulo – SP, com uma turma de 7º ano. A partir disso, foi possível constatar que as brincadeiras além de apresentarem potenciais lúdicos e motivadores, ainda podem auxiliar na promoção do Letramento Estatístico e da criação de Cenários para Investigação. Assim, acredita-se que as brincadeiras mediadas em prol da estatística, auxiliam na construção de cidadãos críticos, proporcionando o empoderamento nas tomadas de decisões.
Palavras-chave: Brincadeiras, Letramento Estatístico, Cenários para investigação.
Resumen
Este texto presenta una investigación que tuvo como objetivo analizar el potencial de los juegos para promover la Alfabetización Estadística. Para ello, señala referentes teóricos sobre Juego y Alfabetización Estadística relacionados con escenarios para la investigación. A partir de estos hitos, esta investigación tiene un carácter cualitativo y se desarrolla bajo el diseño de investigación acción. El corpus está compuesto por observación participante y notas de campo del docente-investigador, considerando momentos de discusión grupal y el desarrollo de la actividad. La investigación se realizó en una escuela municipal de São Paulo – SP, con una clase de 7º grado. A partir de esto, se pudo verificar que los juegos, además de presentar potencial lúdico y motivador, también pueden ayudar a promover la Alfabetización Estadística y la creación de Escenarios para la Investigación. Así, se cree que los juegos mediados a favor de la estadística ayudan en la construcción de ciudadanos críticos, brindando empoderamiento en la toma de decisiones.
Palabras clave: Juegos, Alfabetización Estadística, Escenarios para la investigación.
Abstract
This text presents an investigation aimed at analyzing the potential of games in promoting Statistical Literacy. It provides theoretical references about games and Statistical Literacy related to investigative scenarios. Based on these frameworks, this research is qualitative in nature and follows an action research design. The corpus consists of participant observation and field notes by the teacher-researcher, considering moments of discussion groups and activity development. The research was conducted in a public school in São Paulo - SP, with a 7th-grade class. From this, it was possible to verify that games, besides presenting ludic and motivating potentials, can also assist in promoting Statistical Literacy and the creation of Investigative Scenarios. Therefore, it is believed that games mediated in favor of statistics aid in the construction of critical citizens, empowering them in decision-making processes.
Keywords: Games, Statistical Literacy, landscapes of investigation.
Recibido: 11/12/2023 - Aceptado: 20/05/2024
1. INTRODUÇÃO
A Estatística atualmente pode ser entendida como uma ciência que busca coletar, organizar, analisar e interpretar dados a fim de subsidiar a tomada de decisão (Larson e Farber, 2004). Sua crescente presença na sociedade através das mídias e decisões político-sociais, mostram a relevância de construir cidadãos letrados em Estatística, capazes de ler, compreender, analisar e ter senso crítico acerca das informações que são transmitidas a sociedade. Ao considerar tal pressuposto, torna-se relevante pensar em estratégias e metodologias que promovam tal letramento. Assim, este texto apresenta um recorte de uma pesquisa realizada para mestrado acadêmico em Educação, que ainda está em andamento. O trabalho realizado tem como objetivo analisar a potencialidade de brincadeiras promoverem o Letramento Estatístico.
Autores como Gal (2021) entendem o Letramento Estatístico como uma capacidade que ultrapassa os limites do conhecimento sobre estatística, onde o cidadão deve apresentar requisitos atinentes à conteúdos estatísticos e capacidades relacionadas com a postura em relação a leitura, compreensão, interpretação, avaliação e argumentação de forma crítica das informações estatísticas que lhe são apresentadas. Logo, o Letramento Estatístico está relacionado ao pensamento crítico dos cidadãos. Esses entendimentos podem se relacionar diretamente com a ideia de materacia3 apresentada por Skovsmose (2008), que defende a capacidade de um cidadão interpretar e agir de forma crítica em uma situação social e política estruturada pela Matemática.
Para promover os entendimentos quanto ao Letramento Estatístico, será considerar o brincar como um recurso pedagógico que pode estimular e proporcionar meios de aprendizagem. Kishimoto (2010) entende que esses estímulos, de aprendizagem, vêm por intermédio de habilidades relacionadas ao poder de tomar decisões, expressão de sentimentos e valores, conhecimento de contexto e de solucionar e criar problemas. Além disso, a autora destaca que a brincadeira é uma ação lúdica, emanente do brincante, que gera prazer, alegria e envolvimento de forma voluntária nas tomadas de decisões.
Diante deste contexto, inicialmente será apresentado os referenciais teóricos fundamentadores da pesquisa, atinentes ao Letramento Estatístico relacionado com os cenários para investigação e por último as Brincadeiras. Nos aspectos metodológicos será descrita a atividade desenvolvida, bem como as ações metodológicas que possibilitaram a realização desta pesquisa. A seguir serão apresentados e discutidos os dados produzidos, seguidos das considerações finais
2. APORTES TEÓRICOS
Para iniciar a discussão, vamos explorar o entendimento de Gal (2021) sobre o Letramento Estatístico, que vai além do simples conhecimento de conceitos estatísticos e matemáticos. Embora esses conceitos sejam componentes importantes da formação cidadã, isoladamente não são suficientes para alcançar esse letramento. O autor argumenta que são necessárias tanto a motivação quanto a capacidade de acessar, compreender, interpretar, avaliar criticamente e, quando apropriado, expressar opiniões sobre mensagens estatísticas (Gal, 2002, p. 2). É importante ressaltar que, embora a Estatística seja uma ciência independente (Larson e Farber, 2004), no contexto da Educação Básica, podemos considerá-la como parte da Matemática, já que cabe ao professor de matemática a abordagem dessa ciência em sala de aula.
Essa perspectiva está correlacionada com a teoria da materacia apresentada por Skovsmose (2008), que preconiza não apenas a habilidade de executar cálculos e técnicas, mas também competências para interpretar e atuar em contextos sociais e políticos influenciados pela Matemática. Nesse mesmo sentido, Gal (2021) idealiza um cidadão crítico capaz de agir e tomar decisões na sociedade com base em informações estatísticas. Essa abordagem se assemelha ao conceito de Letramento Estatístico, pois ambos visam à “capacidade de ler e interpretar situações sociais, culturais, políticas, econômicas e compreender essas situações com habilidades para empreender ações transformadoras” (Skovsmose, 2009, p. 111).
Embora para Skvosmose (2000) acredite que não exista uma receita ou passo a passo para um cenário para investigação, iremos considerar os requisitos e critérios propostos ao Letramento Estatístico. Segundo Gal (2002) para um cidadão ser considerado letrado em estatística, o mesmo deve apresentar cinco requisitos que englobam: perceber por que os dados são necessários e como podem ser produzidos; familiaridade com conceitos e ideias básicos relacionados à estatística descritiva; familiaridade com conceitos e ideias básicos relacionados às apresentações gráficas e tabulares; compreender noções básicas de probabilidade; entender como o processo inferencial é alcançado (Gal, 2002, p.10). Além disso, dispõe dois critérios que relacionam a criticidade, leitura, interpretação, argumentação e posicionamento crítico frente às informações estatísticas que o são apresentadas.
Para incentivar o enfoque de tal criticidade, Penteado e Skovsmose (2022) enfatizam a importância da presença de outros ambientes de aprendizagem na educação, considerando uma abordagem de investigação. Para os autores, é importante criar Cenários para Investigação (CI), que se diferenciam fortemente dos paradigmas baseados em exercícios, onde o professor expõe o conteúdo de forma expositiva e fornece aos alunos listas de exercícios. A transição do paradigma de exercícios para cenários de investigação é um movimento que mobiliza estruturas de risco, contudo propicia novas possibilidades. O CI é um ambiente onde o diálogo é de extrema importância, não existem respostas prontas e o professor convida os alunos a emergirem em uma investigação para buscar sanar suas inquietações sobre determinado tema. Penteado e Skovsmose (2022) acreditam que para trabalhar com cenários para investigação, o educador tem que estar preparado para o imprevisível. Além disso, tem que se pautar no diálogo, pois para o autor este desempenha um papel fundamental no estabelecimento de uma atividade crítica.
Para promover tal Cenário para Investigação, será utilizado o brincar como recurso pedagógico potencializador para que realizar o convite aos alunos. Segundo o entendimento de Kishimoto (2010), o brincar é uma ação livre, imanente da criança, sem horários e momentos definidos para ter início. Está ligado à sua essência lúdica e sentimental, que não necessita de algum resultado explícito, podendo envolver, relaxar, desenvolver, ensinar e introduzir a criança no mundo imaginário (Kishimoto, 2010). Assim sendo, como afirma Kishimoto (2010) o brincar tem a prioridade das crianças, sendo a atividade principal do dia a dia, que possuem flexibilidade para ensaiar novas combinações de ideias e de comportamentos.
Podemos observar que a brincadeira está intrinsecamente ligada à subjetividade e à ludicidade. Neste contexto, compreendemos a ludicidade conforme Luckesi (2005), que a define como algo vinculado aos sentimentos, atitudes, prazer e atratividade para o sujeito. Este aspecto varia de indivíduo para indivíduo, uma vez que o que é lúdico e prazeroso para um, pode não ter o mesmo apelo para outro. Deste modo, podemos considerar que o que é uma brincadeira para uma criança, não necessariamente é uma brincadeira a outra. Afinal, o modo de brincar existe em cada criança por natureza (Samuelson e Pramling, 2014).
Samuelson e Pramling (2014) ainda destacam a brincadeira como uma maneira diferente de aprender, onde todas as ações que os brincantes realizam enquanto brincam, os levam a aprender alguma coisa. Contudo é “importante dar voz e autonomia à criança, para que ela tome a decisão sobre o seu brincar, usando seu conhecimento e experiência.” (Garvey, 2015). Seguindo tais entendimentos, a seguir descreveremos os aspectos metodológicos considerados nessa pesquisa.
3. ASPECTOS METODOLÓGICOS
Esta pesquisa se caracteriza como qualitativa (Minayo, 2009) e desdobra-se sob o delineamento de pesquisa-ação. As ações realizadas em sala de aula pelo professor (também autor do texto) foram realizadas com uma turma do sétimo ano do Ensino Fundamental de uma Escola Municipal de São Paulo – SP, a qual o pesquisador estava atuando como professor titular da turma.
Como em uma pesquisa-ação pretende-se encontrar as evidências “a respeito de suas práticas e pressupostos críticos, crenças e valores subjacentes a elas” (Elliot, 2000, p. 209) foram ponderados um conjunto de técnicas e instrumentos de coleta de dados propostos por Coutinho et al (2009) para uma pesquisa-ação. Neste texto apresentaremos parte dos dados coletados, bem como os resultados da pesquisa, considerando que a mesma ainda se encontra em andamento. Assim sendo, as técnicas de Coutinho et al (2009) que iremos considerar são: Grupos de discussão, que são realizadas de forma coletiva com o corpus de pesquisa, por meio da interatividade participantes; A observação Participante, onde o investigador está imbricado no contexto e tem como intencionalidade compreender determinado fenômeno; e as Notas de campo, relacionadas a observação da prática educativa, abrindo a flexibilidade e improviso.
Para melhor entendermos o processo, a seguir descreveremos a brincadeira utilizada na atividade.
3.1. A Brincadeira Rio Vermelho
Para a implementação desta pesquisa-ação, foram considerados os pressupostos teóricos acerca do brincar. Como todo brincar possui regras implícitas e/ou explícitas (Kishimoto, 2010), iremos elucidar a organização da brincadeira que foi levantada pelos próprios alunos. Por ser uma brincadeira da tradição, as regras do brincar podem variar conforme a regionalidade, por esse motivo a seguir iremos descrever como foi brincado pelo grupo corpus de pesquisa. A brincadeira foi organizada dentro de um espaço determinado por duas áreas nas extremidades (áreas seguras), deixando um espaço no meio, delimitado por linhas, para que as crianças “atravessarem” de um lado para o outro. Um aluno deveria se posicionar na área central (entre as duas linhas), o qual foi chamado de “Dono do Rio Vermelho”. O objetivo dos participantes é atravessar de um lado seguro para o outro lado, também seguro, sem serem pegos pelo dono do rio.
Para atravessar o espaço existia uma regra: O dono do rio (pegador) escolhe uma cor, a partir disso, os demais brincantes que estiverem nas áreas seguras buscam tal cor solicitada em suas peças de roupas. Quem possuir alguma peça de roupa na cor escolhida, pode atravessar para a outra área segura (outro lado) sem ser pega pelo dono do rio. Contudo, quem não tiver a cor escolhida deverá correr para o outro lado desviando do pegador. O objetivo do dono do Rio é pegar o maior número de pessoas possíveis. Se o brincante que está atravessando for pego, deverá ficar no lugar exato em que foi segurado pelo dono do Rio Vermelho e poderá auxiliá-lo a pegar os demais colegas, se alguém passar por sua volta. Um aspecto importante a ponderar é que após escolhida a cor, primeiro passam os brincantes que possuem a cor e os demais que não tiverem, aguardam para atravessar juntos.
3.2. A atividade
A atividade foi dividida em três momentos, uma roda de conversa inicial, a construção das estatísticas e uma roda de conversa de fechamento. A seguir descreveremos como os processos foram produzidos os longo das oficinas.
3.2.1. Rodas de conversa
Para iniciar a atividade, todos os alunos foram convidados a brincar coletivamente de forma livre, sem nenhuma interferência do professor. Após o término da brincadeira livre, realizamos uma roda de conversa em que foram levantamos questionamentos a fim de destacar aspectos lúdicos, possíveis pensamentos estatísticos e, além disso, levantar hipóteses para instigar nossas próximas etapas da atividade. A mesma roda de conversa, foi realizada no fechamento da atividade. Contudo, desta vez, nesta rodada os questionamentos tinham a intencionalidade de perceber se o processo foi lúdico e se foi possível evidenciar o potencial da brincadeira com a estatística. Estes momentos foram gravados, entretanto, por este texto se tratar de resultados de uma pesquisa de mestrado, iremos considerar apenas a observação e as notas de campos tomadas pelo professor-pesquisador. Os questionamentos levantados tanto na roda indicial, quanto na de fechamento, estão descritos na Tabela 1.
Tabela 1
Questionamentos levantados nas rodas de conversa
|
Roda de conversa inicial |
Roda de conversa de fechamento |
|
• Qual foi a estratégia usada pelos pegadores (donos do Rio Vermelho)? • Vocês Consideram que foi a melhor estratégia? • Alguém pensou em outra estratégia? Quais? • O que aconteceria se quiséssemos descobrir qual foi o grupo que mais sobreviveu ou o grupo que menos sobreviveu? • Quais estratégias poderíamos utilizar para isso? • Para além do tempo, quais possíveis relações poderíamos considerar? • Foi divertido para vocês a brincadeira? • Você se sentiu envolvido? • Você acredita que é possível aprender brincando? |
• O que você considera que aprendeu com a atividade? • Como foi vivenciar esse processo investigativo? • Construir tabelas, gráficos, medidas de tendencia central, além disso pensar nas estratégias, auxiliou na forma de pensar e visualizar a brincadeira? Por quê? • Foi divertido? • Você acredita que é possível aprender brincando? |
3.2.2. Construindo as estatísticas
Entre as rodas de conversa foi realizado a atividade principal. Nela voltamos a brincar de Rio Vermelho. Contudo desta vez, dividimos a turma igualmente em três equipes de sete alunos. Cada equipe de alunos foi livre para brincar, tendo apenas uma condição: coletar os dados de suas estratégias no início e no final de cada turno da brincadeira. Para isso, uma prancheta com uma planilha foi fornecida para cada grupo. O professor deixou livre para que os alunos decidissem como coletariam as informações. Dois grupos preferiram que o pegador fornecesse os dados e o professor apenas o anotasse na planilha. O outro grupo, contava com uma aluna que estava lesionada e não podia correr ou fazer movimentos bruscos, por esse motivo, a aluna prontamente se disponibilizou a tomar nota para seu grupo, mesmo querendo brincar.
Para que todos os grupos brincassem foi necessária uma hora de aula, sem necessidade de tempo extra. Os grupos brincaram um de cada vez, ou seja, enquanto um grupo estava brincando os demais o observavam. Após o término de todos os turnos de cada grupo, foi instigado aos pegadores (donos do Rio Vermelho) que tomassem nota, atrás da tabela, de qual estratégia utilizaram para escolher a cor. Nos próximos quatro encontros, voltamos à sala de aula reunidos nos mesmos grupos, para construir as ideias dos cinco requisitos apresentados por Gal (2002). Em um encontro refletimos conjuntamente exercendo a escuta e diálogo acerca dos dados coletados. No encontro seguinte os alunos em grupos construíram gráficos de tripla entrada, solicitando o diálogo com o professor quando necessário. No terceiro encontro foi construído as ideias das medidas de tendência central a partir de um mapa mental. No quatro e último encontro, foi apresentado as estatísticas das brincadeiras e refletido acerca dos dados e probabilidades que estavam sendo apresentados. Assim sendo, a coleta de dados de todo caminho trilhado na construção das estatísticas, se deu por meio das anotações do professor e observação dos debates. A seguir, serão apresentados e discutidos os dados levantados nas rodas de conversa considerando todo o processo da pesquisa.
4. APRESENTAÇÃO E DISCUSSÃO DOS RESULTADOS
Nesta sessão será apresentado um relato da experiência apresentando os dados da pesquisa, considerando a observação e narrativa do pesquisador. Por se tratar de um recorte de uma pesquisa de mestrado, a pesquisa ainda está em processo de conclusão e em sua integra apresentará por outros aspectos metodológicos os resultados. Assim, nesse texto apresentaremos os resultados divididos em três momentos, no primeiro contaremos como se iniciou a brincadeira, passamos a construção das estatísticas e finalizamos com o desfecho.
4.1 Iniciando a brincadeira
Como descrito anteriormente, no primeiro momento, os alunos foram convidados a brincar livremente da brincadeira de escolha deles (Rio Vermelho). Os alunos brincaram duas vezes, trocando de pegador entre o processo. Durante o desenvolvimento, observamos outros indícios de construção de conhecimento, que extrapolam apenas a utilização do corpo, estímulo, convívio e interação com os colegas, tomada de decisão e entre outras possibilidades do brincar. Foi possível perceber certa impregnação de conceitos estatísticos e probabilísticos no processo do brincar. Esse movimento se mostrou fluido e imante da criança envolvida na brincadeira.
Em cada turno ao escolher uma cor, o pegador levava em consideração cores frequentes nas roupas dos colegas ou cores mais “improváveis” de algum colega estar utilizando. Embora no momento este processo não fosse muito claro aos alunos, esse movimento de observação e eleição de uma cor, partindo de certa frequência, tem relação com estatística descritiva. Um conceito que é possível destacar é a medida de tendência central moda. Essa medida representa a variável mais frequente no conjunto, associado ao que “mais se repete”. Além disso, também foi possível perceber a mobilização de noções básicas de probabilidade em duas formas. Primeiramente, parte dos alunos externalizaram uns aos outros que a quantidade de roupas utilizadas ou a quantidade de cor que a roupa tiver, seria maior a chance de passarem em segurança. Esses pontos foram possíveis perceber em falas como “Minha meia é colorida, tem todas as cores, nunca vou ser pega”. Outro ponto, foi relacionar as “chances” de passar para o outro lado sem ser pego, com a quantidade de colegas pegos ao longo da brincadeira. Ou seja, quanto mais colegas eram pegos, mais difícil os alunos achavam de atravessar.
Figura 1
Atravessando o Rio Vermelho

Após a brincadeira terminar, foi realizada uma roda de conversa a fim de discutirmos os questionamentos planejados anteriormente, na Tabela 1. Quando questionados em relação às estratégias utilizadas pelos pegadores, os alunos pontuaram que, por vezes, os pegadores não pensavam em alguma estratégia para escolher a cor. Um dos brincantes relatou que escolhia cores “mais difíceis” de se ter em roupas. As estratégias em suma ocorriam de forma inconsciente. Entretanto, ao convidá-los a refletir acerca das estratégias postas, os alunos encontraram outros meios possíveis para se utilizar. Como contar a quantidade de pessoas que utilizam certa cor para escolhê-la. Quando questionados em relação à divisão de grupos, os alunos prontamente contestaram que as estratégias seriam diferentes, afinal segundo eles, cada pegador pensa e age de forma diferente.
Quando questionados qual brincadeira (distinguindo os pegadores) durou mais tempo, todos os alunos concordaram que foi a brincadeira em que um aluno A foi o pegador. Em sequência, ao instigar os alunos a pensarem em estratégias que poderíamos utilizar para encontrarmos qual brincadeira durou mais tempo, grande parte dos alunos pensaram em cronometrar o tempo. Então foram convidados a pensar em outras estratégias, sem utilizar o tempo. Nisso, os alunos pensaram em gravar vídeo das brincadeiras e depois compará-las, observar qual foi o pegador que pegou mais colegas nas primeiras rodadas e também calcular o tempo, baseado em “estatísticas”. Quando questionados o que seriam essas “estatísticas”, nenhum aluno não soube responder, ou seja, pensavam em como solucionar, porém não sabiam como chegar no resultado proposto. Esses momentos mostram a importância da estatística para a percepção do mundo, até mesmo em brincadeiras. Afinal, a brincadeira a qual eles acreditavam durar mais tempo, foi a brincadeira mais rápida.
Quando referido ao lúdico, os alunos, em um contexto geral, consideraram que se divertiram participando da brincadeira. Notoriamente, todos estudantes se envolveram e demonstraram satisfação e felicidade ao brincar. Uma aluna que estava lesionada e optou por assistir a brincadeira, relatou que gostaria de ter brincado e, por isso, não foi divertido. Outra aluna relatou que além de divertido, foi importante para perceber que outras pessoas estavam utilizando as mesmas cores de roupas que ela. A fim de concluir a roda de conversa, foi questionado se os alunos acreditavam que era possível aprender brincando. As respostas dividiram opiniões, parte acreditava que sim, outra parte acreditava que não. Um aluno relatou que em sua opinião “os professores de matemática conseguem estragar a graça dos jogos e brincadeiras que são divertidos”, relatando exemplos relacionados a jogos de tabuleiro e videogame. Para o estudante os professores utilizam tais jogos apenas com o intuito de ensinar algo, deixando de lado o aspecto de diversão que o jogo pode proporcionar. Contudo, ao questionar se a atividade da brincadeira tinha “perdido a graça”, o aluno contestou dizendo “não, mas na próxima aula vai perder”, fazendo referência ao fato de utilizar a brincadeira só com o intuito de ensinar algo. Esta questão foi refeita no fechamento da atividade. O aluno em questão, problematizou “alguns professores” (terminologia utilizada pelo estudante) costumam passar “Pedrinho tem 6670 laranjas em um carro”, sendo nesse momento em que “se perde a graça”. Essa observação apresenta relação aos ambientes de aprendizagem com referência à semirrealidade.
Embora não tenha sido destacado anteriormente, a brincadeira possibilitou o diálogo entre professor e alunos, onde ao serem instigados quanto suas vivências, possibilitou ao professor realizar um convite para um cenário de investigação sobre “O que são essas estatísticas?”. O convite foi aceito pelos alunos quando se motivaram e perceberam que a estatística poderia auxiliá-los em descobrir qual brincadeira durou mais tempo. Após terminar a roda de conversa, no encontro seguinte foram construídas as estatísticas. Estas estão descritas na próxima seção.
4.2. Construindo as estatísticas
No encontro após a roda de conversa, os alunos foram divididos em três grupos, cada um composto por sete alunos. O objetivo desse momento era coletar dados para posteriormente construir as estatísticas. A cada rodada, registrava-se a cor escolhida, o número de colegas com a mesma cor, aqueles que passaram sem serem pegos e quantos foram pegos. Cada grupo participou de uma rodada, variando o número total de rodadas de acordo com o jogador designado. Os dados coletados foram registrados nas tabelas (Figura 2). Durante o processo, foi evidente a presença de ludicidade em todos os momentos, e a coleta de dados ocorreu de maneira fluída. Após a coleta de dados, os grupos discutiram e elaboraram as estatísticas. A seguir, abordarei os possíveis dados relacionados à promoção do Letramento Estatístico, retomando os requisitos e critérios estabelecidos por Gal (2002).
Figura 2
Tabela com os dados coletados
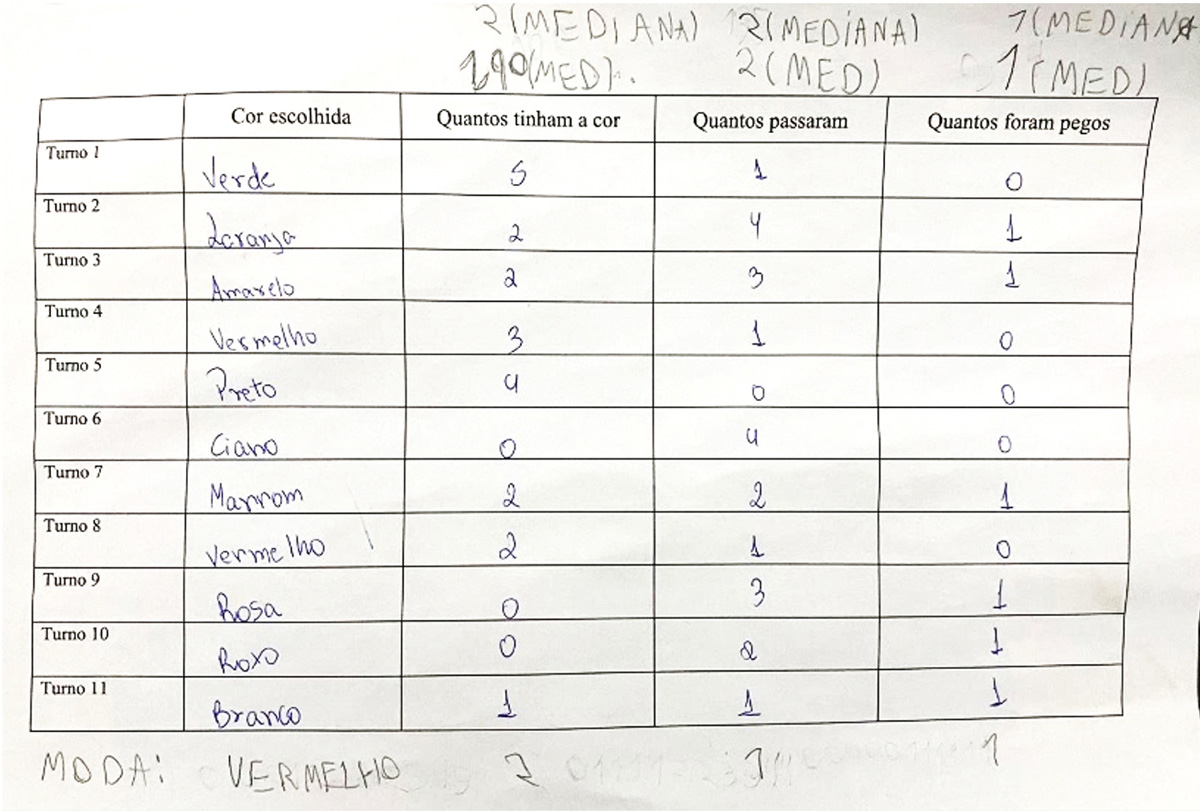
4.2.1. Saber por que os dados são necessários e como os dados podem ser produzidos
Esse requisito traz como evidência dois parâmetros. No primeiro, os alunos demonstraram compreender a importância dos dados quando surgiu o cenário investigativo pautado na estatística. Os alunos tinham como objetivo encontrar qual método poderia ser utilizado para descobrir qual a brincadeira durou mais tempo. Embora alguns alunos cogitassem a ideia de utilizar a estatística para solucionar o problema, ainda assim não demonstravam saber como realizar o processo. Esse movimento pode ter auxiliado na compreensão da necessidade dos dados, afinal como Gal (2002) destaca, é importante a pessoa estar ciente da contribuição de um método de produção de dados, os alunos perceberam que seria necessário “anotar” as informações para dar seguimento a atividade.
No segundo parâmetro, proporcionar a vivência dos alunos produzirem e serem os próprios dados, demonstrou que além de possibilitar o entendimento de como o processo de coleta de dados pode funcionar, também deu sentido ao processo educativo, pontos esses imprescindíveis a Gal (2002). Afinal, abordava uma referência a sua realidade (Skovsmose, 2000), de algo que ele estava motivado a participar. Os alunos notoriamente se envolveram plenamente nessa etapa, pois demandou discussão, ouvir e falar sobre os dados das tabelas com os colegas de seus grupos. Além disso, todos os grupos convidaram o professor para participar das conversas, debatendo e analisando todas as anotações realizadas por rodadas, como demonstra a Figura 3.
Figura 3
Alunos debatendo a coleta de dados

4.2.2. Familiaridade com termos básicos e ideias relacionadas a estatísticas descritivas
Para a discussão deste requisito, que é pautado nas medidas de tendência central, podemos nos valer das construções realizadas pelos alunos durante os encontros. Separados em grupos, nos mesmos que foram realizadas as brincadeiras, os alunos receberam um mapa mental (Figura 4) acerca das medidas de tendência central. Como o contexto da escola incentiva a pesquisa, os alunos já têm o costume de receber a atividade e de forma autônoma pesquisar e debater entre eles o assunto. Após este movimento, chamam o professor para mediar a conversa com o intuito de compartilhar os pensamentos e decidirem qual caminho seguiriam. Em contexto geral, os alunos tiveram facilidade para realizar os cálculos. Porém, foram necessários muitos debates, a fim de compreender os aspectos teóricos por traz das medidas. A moda e a mediana foram as medidas que os alunos apresentaram mais facilidade em compreender como encontram e o que o valor representa. A média foi a medida que necessitou de maior ênfase, nesse momento foram necessários outros exemplos para elucidar os pensamentos. Junto com o professor, foram construídas a média, moda e mediana das idades do grupo, refletindo acerca da variabilidade conforme os dados se modificam.
Figura 4
Mapa mental disponibilizado para os alunos
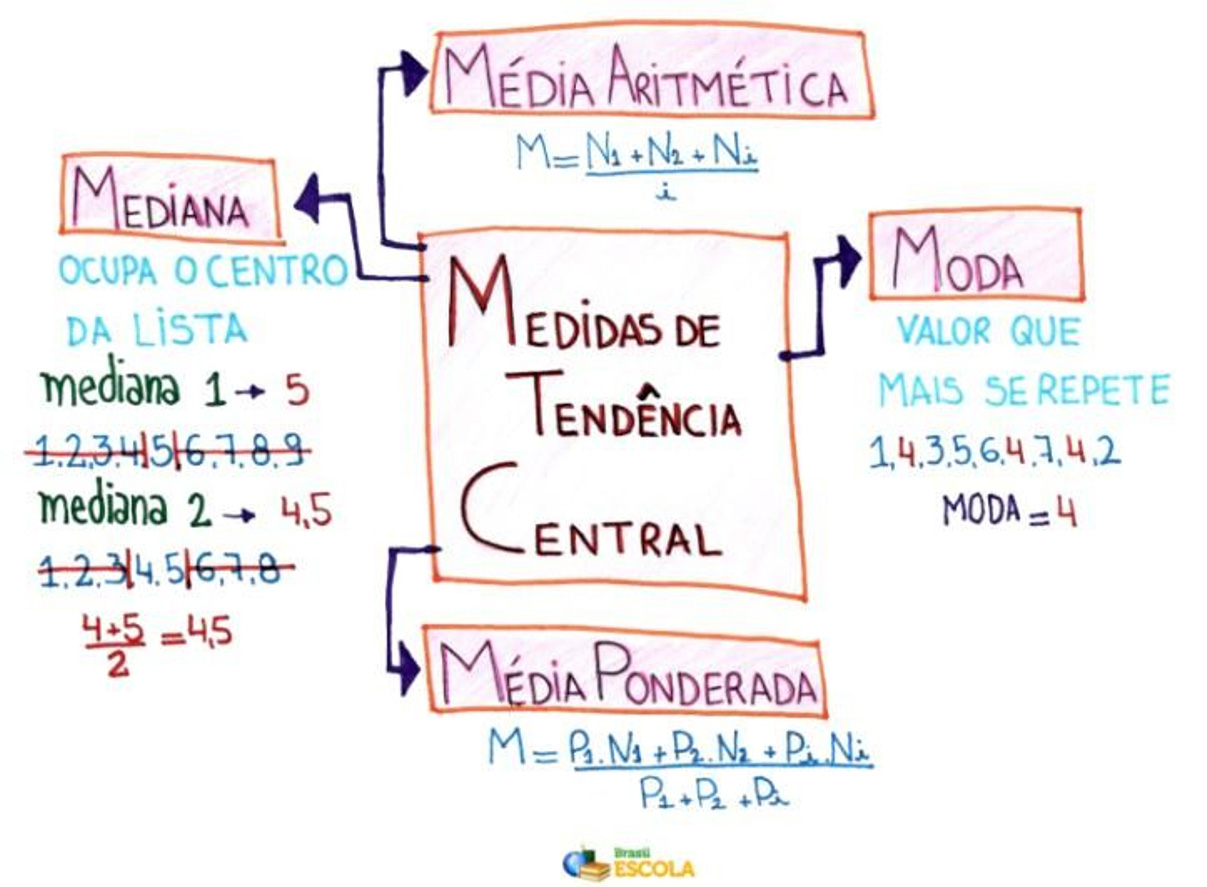
Fonte: Brasil Escola
Após compreendido os conceitos, os alunos iniciaram a construção da moda, média e mediana dos dados coletados em suas brincadeiras. Essas medidas de tendência central são indicadas como um dos principais conceitos para a promoção do requisito, segundo Gal (2002). Como anteriormente os alunos sanaram muitos questionamentos e dúvidas, esse momento ocorreu de forma fluida. Houve poucas dúvidas, o professor manteve a postura de mediador e orientador da aprendizagem. Após terminado os cálculos, foi orientado que os alunos organizassem em uma tabela as medidas encontradas em relação às variáveis selecionadas por eles. Esse material (Figura 5) serviu como suporte para a construção dos cartazes que serão descritos futuramente.
Figura 5
Anotações dos alunos realizando os cálculos das medidas de tendência central
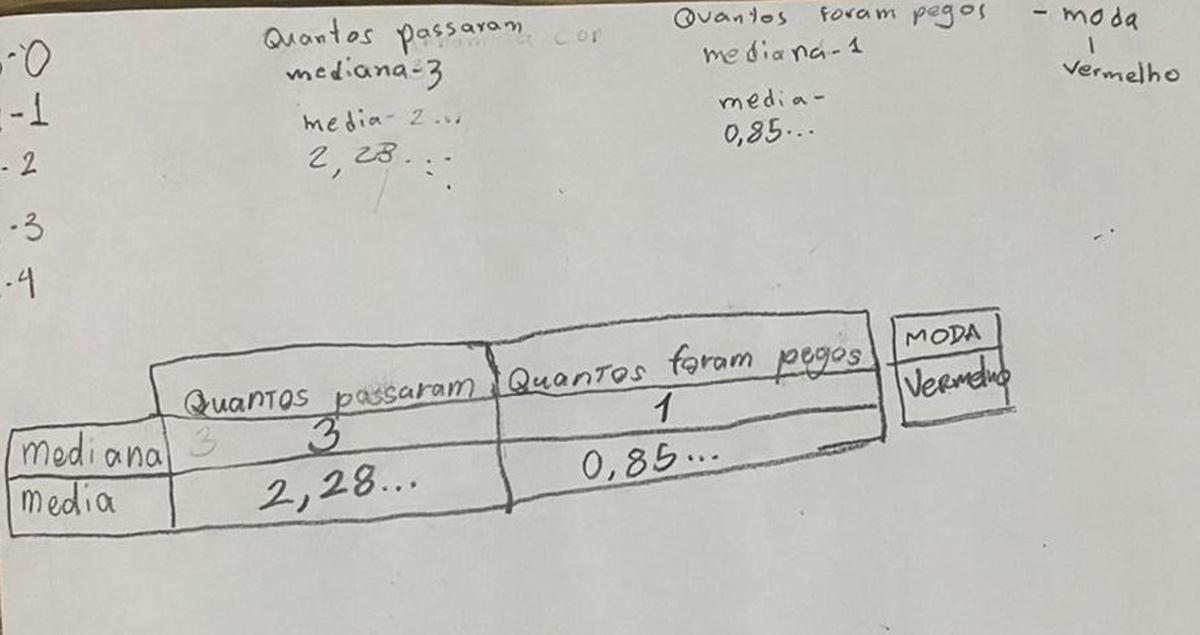
4.2.3. Familiaridade com termos básicos e ideias relacionadas a exibições gráficas e tabulares
Para a construção de gráficos, em um primeiro momento, foi realizada uma discussão acerca dos gráficos apresentados nas mídias de forma inadequada. Era projetado um gráfico e instigado “O que aconteceria se tivéssemos que tomar alguma decisão pautada nesse gráfico?”. Os alunos se mostraram muito entusiasmados em buscar entender os gráficos e possivelmente encontrar erros. A cada gráfico debatíamos o que ele estava querendo dizer e qual seria o jeito mais adequado de apresentá-lo. Ao final, concluímos que todos os gráficos apresentavam certos elementos em comum e com isso delimitamos os elementos principais que compõem um gráfico.
Após essa construção de conhecimento coletiva acerca dos gráficos, foi proposto a construção de um gráfico que poderia ter de duas a três entradas, considerando os dados produzidos pelos alunos nas tabelas. Os alunos tinham como missão apresentar aos colegas as estatísticas de seus grupos para relacionar com a duração das brincadeiras. Dois dos três grupos escolheram realizar um gráfico de três entradas, cruzando a variável cor com a quantidade que tinham a cor, quantos não tinham a cor e quantos foram pegos. O outro grupo escolheu cruzar a cor com quantos tinham a cor e quantos foram pegos. Assim como no processo das medidas de tendência central, os alunos apresentavam certa autonomia em construir os gráficos em um papel craft. O professor atuava como mediador e circulava entre os grupos gerando debates e possíveis alterações em relação à construção gráfica.
Cada grupo decidiu as características de seus gráficos, respeitando seus elementos, porém todos os grupos construíram gráficos de colunas. No mesmo cartaz construíram uma tabela contendo as medidas de tendência central encontradas anteriormente. Notoriamente os alunos pareciam se divertir, por meio da interação e animação ao longo do processo de construção, dividindo funções e colaborando em grupo. Essa construção conversa com a ideia de Gal (2002), já que para esse requisito o autor entende que o cidadão deve saber que os dados podem ser apresentados ou relatados em gráficos e tabulares, realizando também a leitura e interpretação dos dados apresentados nele.
O processo de construção dos cartazes está ilustrado na Figura 6 e os cartazes construídos na Figura 7.
Figura 6
Processo de criação em grupo dos gráficos

Figura 7
Cartazes
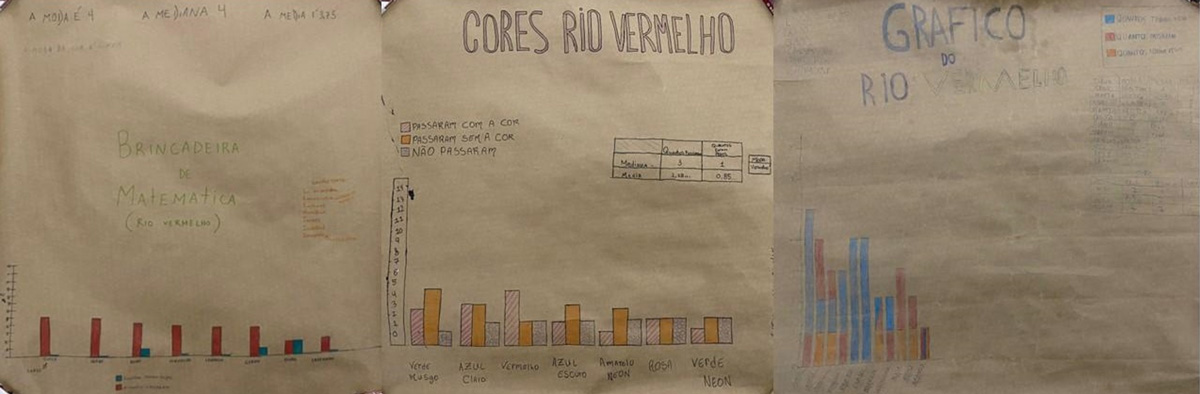
4.2.4. Compreender noções básicas de probabilidade
A promoção do quarto requisito está relacionada com as discussões acerca das ideias do acaso. Após finalizado os cartazes, os alunos organizaram-se em seus grupos com o intuito de realizar uma apresentação das estatísticas para seus colegas. Após o encerramento de cada apresentação, o professor gerava debates envolvendo a palavra “chance”, que se demonstrou habitual para os alunos. Afinal, como Gal (2002) afirma, ideias relacionadas ao acaso e eventos aleatórios, fazem parte deste requisito. Ao longo do processo, os alunos demonstraram certo interesse em refletir sobre as chances de certas situações acontecerem. Partindo disso, foi pensado acerca da chance de uma cor ser escolhida, as chances de ser pego, o que aconteceria se o número de brincantes fosse menor e outras pautas que surgiram ao longo do debate. As classificações pautavam em muito provável, improvável, talvez aconteça e outros sinônimos abordados pelos alunos. Embora não se intencionasse realizar o cálculo de probabilidade, os alunos demonstraram certo interesse e se motivaram com o tema. Esse movimento gerou um cenário de investigação acerca da probabilidade, que foi realizado posteriormente a aplicação da atividade de pesquisa.
4.2.5. Saber como conclusões ou inferências estatísticas são alcançadas
A promoção do quinto requisito engloba todo o processo de construção das estatísticas. Os alunos brincaram, produziram e coletaram dados, analisaram as medidas de tendência central e frequências, refletiram sobre o acaso e por fim apresentaram suas estatísticas (Figura 8). Para a apresentação os alunos, em grupos, expuseram seus cartazes aos demais colegas e apresentaram suas análises em relação aos dados. Realizaram a leitura dos gráficos, medidas de tendência central e também suas conclusões em relação ao processo. Durante os debates, após a apresentação, os alunos pautaram as discussões a partir de suas visões e dados produzidos.
A turma concluiu que, embora os dados fossem apresentados de formas diferentes, os gráficos mostravam a mesma intencionalidade, especificados nas mesmas variáveis. Também perceberam que o modo utilizado para a apresentação indica a interpretação dos dados para tentar descobrir qual brincadeira durou mais tempo. Segundo os alunos, essa interpretação é pessoal e pode variar dependendo do entendimento da pessoa que estiver lendo. Porém, concluíram que o grupo B teria o menor tempo, pois contaram com menos rodadas e mais pessoas pegas ao longo de cada turno. Esse processo de discussão e busca por respostas, conversam com o entendimento de Gal (2002) quanto ao requisito, pois para o autor os alunos dem ter a noção de como os dados são analisados (através das medidas e gráficos) e as conclusões alcançadas (como o grupo com o menor tempo), além de estarem atentos a possíveis erros e manipulações que os colegas poderiam cometer ou realizar.
Figura 8
Apresentação dos grupos

Ao longo de todo o processo de construção dos dados, os alunos se mostraram argumentativos e analíticos. Apontavam erros e indicavam melhorias. Ao observar todos os momentos, foi possível destacar que os alunos buscaram uma postura ativa durante a aplicação da atividade. Também colaboraram com opiniões e argumentos pautados nos dados que foram coletados. Esses apontamentos podem estar relacionados às duas capacidades abordadas por Gal (2002), segundo as quais um cidadão deve interpretar e avaliar criticamente informações estatísticas e discutir ou comunicar suas reações a tais informações.
Ao ponderar todos os pontos levantados nessa etapa, podemos considerar a potencialidade de promover o letramento estatístico por meio de brincadeiras. A seguir, será descrito o fechamento da atividade.
4.3. Desfecho da atividade
Após a finalização das apresentações e debates, realizamos nossa última roda de conversa acerca da atividade. Nela os alunos conversaram acerca do que aprenderam, pontuando com maior frequência gráficos e as medidas de tendência central. Em um contexto geral, todos externalizaram ter gostado da atividade, principalmente dos momentos de construir gráficos e de brincar. Segundo seus discursos, os alunos gostaram da ideia de envolver a matemática com brincadeira, para eles foi importante brincar e mesmo assim descobrir mais coisas de matemática e se divertindo. Uma aluna enfatizou não acreditar que tinha estudado com a brincadeira Rio Vermelho. Após tais relatos, voltei a perguntar se a matemática tinha “estragado a brincadeira” como eles disseram na primeira roda de conversa. Os alunos disseram que não estragou a brincadeira e que acharam interessante brincar e depois estudar matemática embasada na vivência.
Além dos aspectos levantados, os alunos também perceberam que a estatística pode ser utilizada ao longo da brincadeira, a fim de auxiliá-los no processo do brincar. De acordo com seus pensamentos, o pegador pode valer-se da frequência ou moda das cores para pensar em sua estratégia. Como exemplo, escolher a cor que mais se repete (moda) para que passe em segurança um número maior de pessoas, para que o pegador possa focar em pegar o grupo menor na travessia. Por fim, o que antes estavam divididos, agora todos os alunos passaram a acreditar que é possível aprender brincando, basta saber mediar o processo educativo.
5. CONSIDERAÇÕES FINAIS
Nesta pesquisa, buscou-se analisar, por meio de uma pesquisa-ação, a potencialidade de brincadeiras promoverem o Letramento Estatístico. Para isso, foi aplicada uma atividade com uma turma do 7º ano do Ensino Fundamental. A brincadeira utilizada foi a do Rio Vermelho. A coleta de dados se deu por meio de rodas de conversa, observação participante e notas de campo do professor-pesquisador.
Durante a pesquisa, ficou evidente que as brincadeiras podem ser aliadas significativas na criação de cenários para investigação. Além disso, quando mediadas por meio do diálogo, escuta, criticidade e trabalho em grupo, conforme discutido por Skovsmose (2008), acredita-se que seja possível promover o Letramento Estatístico. Isso ocorre porque os alunos passam a compreender como os dados são produzidos e sua importância, ganham familiaridade com gráficos, tabelas e medidas de tendência central, discutem sobre noções de acaso e compreendem como o processo inferencial pode ser alcançado, conforme enfatizado por Gal (2002). Assim, as brincadeiras não apenas movimentam o corpo, mas também auxiliam na interação social, divertem e motivam os alunos no processo de aprendizagem.
Após brincar livremente, construir estatísticas e refletir acerca do processo, foi possível perceber que os alunos se tornaram mais críticos seja nas brincadeiras, como também em outros contextos. As brincadeiras abrem caminhos a serem instigados, cabe ao professor realizar o convite no momento oportuno para que os alunos se sintam instigados a aceitá-lo. não estragou e que acharam interessante brincar e depois estudar matemática embasada na vivência.
Assim, por se tratar de considerações iniciais dos dados coletados para uma pesquisa de mestrado, ainda será acrescentado: novos pensadores no referencial teórico; construção dos episódios por meio dos discursos com a transcrição dos áudios; apresentar os dados produzidos nos vídeos e áudios, bem como a análise deles; acrescentar novas reflexões. Estas serão apresentadas na integra, com mais detalhes na produção cientifica final do autor desse texto.
REFERENCIAS
Coutinho, C. Souza, A., Dias, A., Bessa, F., Ferreira, M. e Vieira, S. (2009). Investigação-acção: metodologia preferencial nas práticas educativas. Psicologia, Educação e Cultura, 13(2), 445-479.
Elliot, J. (1991). Action research for educational change. Open University Press.
Gal, I. (2002). Adult numeracy development: theory, research, practice. Hampton Press.
Gal, I. (2021). Promoting statistical literacy: Challenges and reflections with a Brazilian perspective. En C. Monterio y L. Carvalho (Eds.), Temas emergentes em letramento estatístico (pp. 37-59). UFPE.
Garvey, C. (2015). A brincadeira: a criança em desenvolvimento. Editora Vozes.
Kishimoto, T. (2010). Brinquedo e brincadeiras na educação Infantil. I Seminário Nacional: Currículo em Movimento - Perspectivas Atuais (pp. 1-20). Ministério da Educação.
Larson, R. e Farber, B. (2004). Estatística Aplicada. Pearson Prentice Hall.
Luckesi, C. (2005). Brincar III: a criança e sua poética. (Material obtido através do website de Cipriano Carlos Luckesi).
Minayo, M. (2009). O desafio da Pesquisa Social. En M. Minayo (Ed.), Pesquisa Social: teoria, método e criatividade (pp. 9-29). Vozes.
Penteado, M. e Skovsmose, O. (2022). Entering Landscapes of Investigation. En M. Penteado e O. Skovsmose (Eds.), Landscapes of Investigation (pp. 1-20). Open Book Publishers.
Samuelson, I. e Pramling, N. (2015). Children´s Play and Learning and Developmental Pedagogy. En L. Brooker, M. Blaise e S. Edwards (Eds.), The SAGE Handbook of Play and Learning in Early Childhood. SAGE Publishing.
Skovsmose, O. (2000). Cenários de investigação. BOLEMA, Boletim de Educação Matemática, 13(14), 66-91.
Skovsmose, O. (2008). Desafios da reflexão em educação matemática crítica. Papirus.
Como citar:
Barcarolo, P. y Milani, R. (2024). O brincar e o letramento estatístico: um possível cenário para investigação? Revista de Educación Estadística, 3, 1-20. https://doi.org/10.29035/redes.3.1.4

Esta obra está bajo una licencia de Creative Commons
Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional.
1*Autor de correspondencia: barcarolopedro@gmail.com (P. Barcarolo)
https://orcid.org/0000-0003-1001-6164 (barcarolopedro@gmail.com).
3 Também apresentada como matemacia em outras obras de Skovsmose.
