Revista de Educación Estadística https://revistaeduest.ucm.cl/ Vol. 3, pp. 1-25, ene. 2024 - dic. 2024 ISSN 2810-6164

DOI: https://doi.org/10.29035/redes.3.1.2

 

ESTRATEGIAS METODOLÓGICAS PARA MEJORAR EL CONOCIMIENTO ESPECIALIZADO SOBRE LA ENSEÑANZA DE LA ESTADÍSTICA

Estratégias metodológicas para melhorar o conhecimento especializado sobre o ensino de estatística

Methodological strategies for improving specialized knowledge on teaching of statistics

Joan Franco Seguí1

Universitat de Girona (Girona, España)

Ángel Alsina2

Universitat de Girona (Girona, España)

 

Resumen

A partir de los resultados de una investigación previa en la que, desde el modelo Mathematical Teacher’ Specialized Knowledge (MTSK), se ha analizado el conocimiento especializado del profesorado de educación primaria sobre la enseñanza de la estadística, se ofrecen distintas estrategias metodológicas con el propósito de enlazar dichos resultados con la práctica escolar. Para cada subdominio de conocimiento, primero se presenta una breve descripción y una síntesis de los principales resultados del estudio preliminar y, seguidamente, se ofrecen distintas estrategias metodológicas contextualizadas a partir de un proceso de formación o una actividad en particular, para que el profesorado pueda llevar a cabo una mejora en la planificación y gestión de las tareas estadísticas y una enseñanza más eficaz. Se concluye que el uso de distintas metodologías (Lesson Study, Flipped Classroom, reflexión sobre la práctica, diseño de tareas, entre otras) puede contribuir a mejorar el conocimiento especializado del profesorado para enseñar estadística y, por consiguiente, mejorar el desarrollo de la alfabetización estadística del alumnado de educación primaria.

Palabras clave: Enseñanza de la estadística, Conocimiento especializado del profesorado de matemáticas, Estrategias metodológicas, Educación primaria.

 

Resumo

Com base nos resultados de uma investigação anterior em que, a partir do modelo Mathematical Teacher’s Specialized Knowledge (MTSK), foi analisado o conhecimento especializado dos professores do ensino básico sobre o ensino da estatística, são propostas diferentes estratégias metodológicas com o objetivo de relacionar estes resultados com a prática escolar. Para cada subdomínio do conhecimento, começa-se por apresentar uma breve descrição e uma síntese dos principais resultados do estudo preliminar e, em seguida, são propostas diferentes estratégias metodológicas contextualizadas a partir de um determinado processo ou atividade de formação, a fim de permitir que os professores melhorem o planeamento e a gestão das tarefas estatísticas e ensinem mais eficazmente. Conclui-se que a utilização de diferentes metodologias (Lesson Study, Flipped Classroom, reflexão sobre a prática, desenho de tarefas, entre outras) pode contribuir para melhorar o conhecimento especializado dos professores para ensinar estatística e, consequentemente, melhorar o desenvolvimento da literacia estatística nos alunos do ensino básico.

Palavras-chave: Ensino da estatística, Conhecimento especializado dos professores de matemática, Estratégias metodológicas, Ensino básico.

 

Abstract

Based on the results of a previous research in which, from the Mathematical Teacher’s Specialized Knowledge (MTSK) model, the specialized knowledge of primary school teachers on the teaching of statistics has been analyzed, different methodological strategies are offered with the aim of linking these results with school practice. For each sub-domain of knowledge, first a brief description and a synthesis of the main findings of the preliminary study is presented, and then different methodological strategies contextualized from a particular training process or activity are offered to enable teachers to improve the planning and management of statistical tasks and to teach more effectively. It is concluded that the use of different methodologies (Lesson Study, Flipped Classroom, reflection on practice, task design, among others) can contribute to improve teachers’ specialized knowledge to teach statistics and, consequently, improve the development of statistical literacy in primary school students.

Keywords: Statistics teaching, Specialized knowledge of mathematics teachers, Methodological strategies, Primary education.

Recibido: 05/12/2023 - Aceptado: 20/04/2024

 

1. INTRODUCCIÓN

Las investigaciones sobre el conocimiento del profesorado han ido en auge desde los planteamientos de Shulman (1987), que pretendía determinar el “conocimiento base” requerido para la enseñanza con la finalidad de explicar y describir los componentes del conocimiento profesional. A partir de sus planteamientos, han ido surgiendo distintos modelos sobre el conocimiento del profesorado para enseñar matemáticas, como el Mathematical Knowledge for Teaching (MKT) de Ball et al. (2008), el modelo de Conocimientos y Competencias Didáctico-Matemáticas (CCDM) de Godino et al. (2017) o el Mathematical Teacher’s Specialized Knowledge (MTSK) de Carrillo et al. (2018), entre otros.

Este artículo se focaliza en el conocimiento del profesorado para enseñar estadística, pues diversos investigadores han constatado la importancia de este tema y la escasa preparación del profesorado (Bakker et al., 2021). En esta misma línea, una revisión de la literatura científica realizada por Franco y Alsina (2022a) ha evidenciado las dificultades del profesorado de educación primaria para enseñar estadística (e.g., Estrella et al., 2015; Koleza y Kontogianni, 2012; Siswono et al., 2018; Watson et al., 2008), al sentirse poco preparados para resolver las posibles dificultades del alumnado (Batanero, 2009). Estos datos confirman la necesidad de abordar esta problemática para promover una construcción significativa del conocimiento estadístico en las aulas de educación primaria. En este sentido, aquí se asume que además de comunicar los resultados de investigaciones en congresos o revistas científicas de impacto internacional, surge la necesidad de ofrecer orientaciones didácticas en revistas y/o libros de divulgación para que el profesorado en activo pueda llegar a ellos con más facilidad (Vásquez y Alsina, 2022). Esta transferencia puede contribuir a la mejora de las prácticas de enseñanza.

Desde este marco, el trabajo que se presenta parte de los resultados del estudio de Franco y Alsina (2024), en el que se han analizado los conocimientos del profesorado de educación primaria para enseñar estadística. Con este propósito, los autores diseñaron y validaron previamente el cuestionario MTSK-Estocástico/Estadística (Franco y Alsina, 2023) para analizar los conocimientos del profesorado desde los dominios y subdominios del modelo MTSK (Carrillo et al., 2018). Adicionalmente, se han considerado también los planteamientos del Enfoque de Itinerarios de Enseñanza de las Matemáticas (EIEM) propuesto por Alsina (2018, 2019, 2020). Este enfoque propone secuencias de enseñanza intencionadas que contemplan tres niveles: informal (situaciones cotidianas y recursos manipulativos), intermedio (juegos, recursos tecnológicos) y formal (recursos gráficos y literarios), aspecto que ha sido considerado en los diversos ítems del cuestionario.

Con el objetivo de tratar de enlazar los resultados obtenidos en esta investigación con los conocimientos del profesorado de educación primaria para enseñar estadística, en lo que sigue se considera la siguiente estructura para cada uno de los subdominios del MTSK: primero se describe sintéticamente cada subdominio y los principales resultados obtenidos; y, luego, se ofrecen orientaciones didácticas para mejorar las prácticas de enseñanza con base en los resultados obtenidos.

 

2. CONOCIMIENTO DE LOS TEMAS (KoT)

 

2.1. Descripción del subdominio y principales resultados

 

De modo general, dentro de la agenda de investigación en educación matemática sobre el conocimiento del profesorado para enseñar matemáticas, se asume que el profesorado debe conocer los contenidos que enseña al alumnado. Para describir qué y cómo conoce el profesorado los contenidos, en el modelo MTSK se considera el subdominio KoT, que implica saber los contenidos matemáticos y sus significados fundamentados (Flores-Medrano et al., 2014). En este sentido, el profesorado debe tener un nivel de profundización, organización y estructuración superior al que tendrá el alumnado, para poder realizar una enseñanza de manera eficaz. El modelo MTSK recoge cinco categorías para caracterizar el KoT: 1) Fenomenología, en otras palabras, el conjunto de situaciones en las que el profesorado ubica el tema y el conocimiento de los usos y aplicaciones del tema (Liñán et al., 2016); 2) Propiedades y sus fundamentos, se incluyen tanto los procesos matemáticos que enuncian propiedades, teoremas… como sus demostraciones y todo lo referente a la axiomática; 3) Registros de representación, hace referencia al conocimiento que tiene el profesorado sobre las distintas formas de representar el tema (numérica, gráfica, verbal, …) ; 4) Definiciones, se considera el conocimiento de las distintas propiedades que hacen definible a un objeto determinado (Flores-Medrano et al., 2014); y, 5) Procedimientos, se incluye el conocimiento de algoritmos, su utilización y sus fundamentos.

En Franco y Alsina (2022b) se caracterizó el KoT para enseñar estadística, dando lugar al Conocimiento de los Temas Estadísticos (CTE). En este sentido, los autores argumentan que el profesorado debe comprender la terminología básica (población, muestra, variable estadística, entre otras) y comprenderla en un contexto para, posteriormente, cuestionar las afirmaciones hechas sin una justificación estadística adecuada (Watson, 1997; Franco y Alsina, 2022b). Además, el profesorado debe comprender por qué se necesitan datos; estar familiarizado con términos e ideas básicas de la estadística descriptiva y con gráficos y tablas; comprender las nociones de probabilidad; y, finalmente, saber llegar a inferencias estadísticas (Gal, 2002; Burrill y Biehler, 2011; Franco y Alsina, 2022b).

En el estudio de Franco y Alsina (2024), se investigó el CTE a partir del cuestionario previamente validado MTSK-Estocástico/Estadística (Franco y Alsina, 2023). Los resultados obtenidos revelan que el profesorado desconoce algunos de los contenidos estadísticos que debe enseñar a su alumnado, presentando un conocimiento deficiente y, en algunos casos, muy deficiente, pues la puntuación media es de 41,6 sobre 100. A partir de estos datos, se evidencia que los participantes no tienen el nivel de profundización y organización de los temas que deberían tener para enseñar de manera eficaz la estadística. Con relación a los contextos de enseñanza propuestos por el EIEM, en este subdominio de conocimiento se han identificado mejores puntuaciones en los ítems involucrados con los juegos, pero preocupan las bajas puntuaciones en los ítems con situaciones reales, pues algunos autores manifiestan la necesidad de usar contextos reales, significativos y motivadores para el alumnado para promover una enseñanza eficaz de los contenidos de estadística (Alsina, 2020; Alsina et al., 2020).

 

2.2. Estrategias metodológicas

 

Las bajas puntuaciones identificadas en relación con el CTE pueden deberse a la poca formación inicial sobre estadística (Franklin y Mewborn, 2006); en otras palabras, no han recibido una formación adecuada para realizar una enseñanza eficaz en las aulas (Vásquez y Alsina, 2015; Batanero, 2001). En este sentido, se propone diseñar programas de formación que promuevan el CTE a partir de la creación de entornos de aprendizaje, estrategia que se centra en desarrollar prácticas de instrucción para la clase de matemáticas a partir de juegos de rol, creación de cuentos, diseño de tareas matemáticas, etc., con la finalidad de enriquecer el proceso de enseñanza-aprendizaje y avanzar hacia la identificación de las cinco categorías que caracterizan el KoT y, por extensión, el CTE (Fenomenología, propiedades y sus fundamentos, representación, definiciones y procedimientos). Por ejemplo, Marimón et al., (2021) muestran que, a partir de un proceso de formación en el que los futuros docentes elaboran secuencias didácticas, progresivamente movilizan una mejor competencia de análisis didáctico.

A continuación, a modo de ejemplo, se describe un juego de rol como estrategia para la creación de un entorno de aprendizaje, con el objeto de simular la enseñanza de la estadística entre los distintos participantes (en este caso, podría ser necesario grabar el desarrollo del juego de rol para un posterior análisis). La representación del juego de rol consiste en la simulación de una clase de sexto de primaria donde asisten los estudiantes y un docente que, a partir de una situación planteada, debe resolver las dudas del alumnado. Teniendo en cuenta los colectivos implicados, se definen distintos roles que son asignados a distintos grupos de participantes, de entre tres y cuatro miembros. En este sentido, la clase contará con dos estudiantes con altas capacidades, dos estudiantes NESE (Necesidades Específicas de Soporte Educativo), tres con muchas dificultades y diez que van siguiendo la clase. Además, los docentes que no participan del juego de rol son los observadores del juego. El formador plantea la siguiente situación ficticia:

En una clase de 30 estudiantes se les preguntó cuántas horas al día pasan en línea. Los resultados se muestran en la Tabla 1:

 

Tabla 1

Datos de las horas que pasan en línea

Horas en línea	Estudiantes
1	5
2	7
3	8
4	6
5 o más	4

 

Con la finalidad de indagar acerca del CET, se solicita que realicen cálculos de la media, mediana y moda del número de horas que el alumnado pasa en línea, para después analizar la variabilidad de los datos obtenidos.

Ante esta situación, el participante que tiene el rol de docente debe ir resolviendo las distintas dudas que puede tener el alumnado. En este sentido, a los participantes con rol de estudiante se les proporcionan distintas preguntas que pueden ir haciendo durante el transcurso del juego, destacando que pueden añadir o eliminar según vean conveniente.

Posibles preguntas:

• ¿Cuál es la diferencia entre la media, la mediana y la moda?

• ¿Qué es la desviación estándar y cómo se calcula?

• ¿Qué es la correlación estadística y cómo se mide?, ¿en los datos proporcionados, existe correlación entre las horas en línea y el número de estudiantes?

• ¿Qué registros de representación identificas en la actividad?, ¿Resultan ser favorables para el tema?

• ¿Qué definiciones y propiedades encuentras en la actividad?, ¿Son correctas?

Al terminar la escenificación, es importante sintetizar y clarificar el registro de los observadores, las dudas que han registrado, los comentarios y/o aciertos que han percibido durante el transcurso del juego. Una vez terminado el debate, se proporciona la grabación en vídeo del juego al participante con rol de docente para que observe y analice su escenificación y, por tanto, su explicación de las distintas dudas que han ido surgiendo. Este punto es muy importante ya que, de acuerdo con Korthagen (2001), el profesorado debería disponer de criterios para saber cuándo, qué y por qué algo es conveniente y deberían reflexionar sobre ello: en el caso del juego, las distintas explicaciones realizadas y la solución de las dificultades que se ha encontrado durante el proceso de enseñanza-aprendizaje.

 

3. CONOCIMIENTO DE LA ESTRUCTURA MATEMÁTICA (KSM)

 

3.1. Descripción del subdominio y principales resultados

 

En el modelo MTSK, el Conocimiento de la Estructura Matemática hace referencia a las distintas conexiones matemáticas que permiten al profesorado comprender y desarrollar conceptos más avanzados desde una perspectiva elemental y conceptos básicos mediante una visión avanzada (Aguilar et al., 2013). En este sentido, las distintas conexiones promueven que el profesorado comprenda en mayor medida las matemáticas, desde la perspectiva de una mayor adquisición de contenido y su posterior organización. En definitiva, este subdominio aborda las conexiones transversales a partir de una vinculación epistemológica entre los distintos conceptos (Muñoz-Catalán et al., 2015).

Considerando la caracterización del Conocimiento de la Estructura Estadística (CEE) de Franco y Alsina (2022b), el profesorado debería considerar las distintas medidas (centro, dispersión, forma, entre otras) y las distintas representaciones bajo un determinado contexto (Vidal-Szabó y Estrella, 2019). Además, es importante que el profesorado realice conexiones entre la estadística y la probabilidad mediante el muestreo de un estudio inferencial. En otras palabras, al recoger datos de una parte de la población, a partir de la estimación y contraste de hipótesis, los resultados pueden generalizarse a la población a través de una investigación inferencial. Finalmente, el profesorado debe tener en cuenta la estabilidad que adquieren las frecuencias relativas asociadas a cualquier suceso cuando se aumenta el número de repeticiones (Ley de los Grandes Números) fundamentado en el enfoque frecuencial de la probabilidad (Canal y Jaimes, 2013)

En la investigación realizada por Franco y Alsina (2024), los datos del CEE son muy deficientes, al tener una puntuación media de las puntuaciones normadas de 36,6 sobre 100. De estos resultados se puede inferir que el profesorado tiene serias dificultades para realizar conexiones de los conceptos básicos con los más avanzados. Respecto al papel de los contextos de enseñanza propuestos por el EIEM, los resultados de la investigación previa manifiestan que el profesorado obtiene mejores puntuaciones en ítems en los que hay involucrados juegos, mientras que las puntuaciones más bajas se obtienen en los ítems diseñados a partir de contextos reales.

 

3.2. Estrategias metodológicas

 

Desde una perspectiva genérica, es imprescindible proponer actividades en las que existan una amplia variedad de conexiones o herramientas para garantizar que los estudiantes puedan conectar los conocimientos previos con los nuevos y reorganizar y construir nuevos aprendizajes.

Ante los débiles resultados con relación al CEE, se propone diseñar un proceso formativo de distintos módulos que centrará la atención en la profundización sobre el contenido estadístico implicado en la realización de los procesos del ciclo de investigación estadística: resolución de problemas, formulación de preguntas, la recogida de datos, el análisis de los datos y la interpretación de los resultados.

A modo de ejemplo, se desarrolla un módulo formativo a partir del realizado por Azcárate y Cardeñoso (2011), estructurado en seis módulos:

• En los módulos 1-3, la atención se centra en la profundización sobre el contenido estadístico y las distintas conexiones entre los contenidos estadísticos y matemáticos implicados en la resolución de problemas, en la formulación de preguntas, la recogida de datos, el análisis de los datos y la interpretación de los resultados.

• En los módulos 4- 6, el foco se centra en la aplicación en el aula para trabajar las distintas conexiones para obtener una mayor adquisición y mejor organización del contenido. El profesorado, a partir de los módulos 1-3, en el módulo 4 debe personalizar y ampliar los materiales que se presentan y diseñar su propio escenario; en el módulo 5, los aplica en su propia aula con el apoyo del equipo de formadores; y, por último, una vez se ha implementado la tarea o actividad diseñada, en el módulo 6 se realiza la evaluación del proceso de enseñanza en el aula a partir de la metodología de la reflexión sobre la práctica, para que el profesorado pueda cuestionar sus propias actividades y estrategias, identificar fortalezas y debilidades, desarrollar nuevas habilidades y conocimientos. Desde esta perspectiva, la destrucción, la co-construcción y la reconstrucción de conocimientos son procesos fundamentales que permiten adquirir consciencia de qué conocimientos (en nuestro caso, sobre el CEE) son un impedimento para la construcción de su identidad personal, compartirlo en comunidades de práctica y, posteriormente, transformarlo en conocimiento profesional (Melief et al., 2010).

Para promover estos procesos de deconstrucción, co-construcción y reconstrucción del CEE, en el contexto de un problema real que permita reconocer el tipo de variables en juego se pueden plantear preguntas como las siguientes:

• ¿En qué consiste la estadística descriptiva?

• ¿En qué consiste la inferencia estadística?

• ¿Qué es la regresión lineal?

• ¿Qué es mejor, tener buenos datos o buenos modelos? Y, ¿cómo se define “bueno”?

• ¿Qué es una “distribución normal”?

• ¿Identificas nociones o conceptos en la actividad que se complementen entre sí?

• ¿Cómo evoluciona el concepto de media hasta llegar a sexto de primaria?

 

4. CONOCIMIENTO DE LA ENSEÑANZA DE LAS MATEMÁTICAS (KMT)

 

4.1. Descripción del subdominio y principales resultados

 

En el MTSK (Carrillo et al., 2018), el Conocimiento de la Enseñanza de las Matemáticas (KMT) incluye las distintas estrategias que el profesorado puede considerar en el proceso de enseñanza-aprendizaje y, de esta forma, fomentar un desarrollo de las matemáticas procedimentales o conceptuales (Flores-Medrano et al., 2013). En este subdominio, se incluyen los conocimientos de recursos materiales o virtuales, el conocimiento de estrategias de enseñanza (técnicas, tareas y ejemplos) y, finalmente, el conocimiento de teorías personales o formales de enseñanza (Montes et al., 2019).

En Franco y Alsina (2022b) se adapta el subdominio KMT a la enseñanza de la estadística, denominándolo Conocimiento de la Enseñanza de la Estadística (CENE). Según Gal (2002), el profesorado debe centrar la enseñanza de la estadística desde dos factores interrelacionados: 1) capacidad para interpretar y evaluar críticamente los datos estadísticos; 2) Capacidad de discutir o comunicar sus opiniones sobre informaciones estadísticas. Más adelante, en el informe Statistical Education of Teachers de la American Statistical Association (ASA, 2015), se indica que el profesorado debe: dar sentido a los problemas; dar estrategias para razonar de forma abstracta y en presencia de la variabilidad y permitir la variabilidad en los datos en relación con un contexto particular; guiar en la construcción de argumentos viables y ser crítico con el razonamiento del resto; y dotar de estrategias con el objetivo de que el alumnado utilice las herramientas adecuadas para resolver un problema estadístico; entre otras recomendaciones. Adicionalmente, es conveniente resaltar que en la literatura existen otros referentes que guían la enseñanza de la estadística, como el informe GAISE II (Bargagliotti et al., 2020), en el que se indican distintos factores para promover la alfabetización estadística del alumnado desde el marco de la resolución de problemas: 1) Formular preguntas de investigación estadística; 2) Recopilar/considerar datos; 3) Analizar datos; 4) Interpretar datos.

Desde esta perspectiva, en la investigación de Franco y Alsina (2024) se analiza el conocimiento del profesorado con relación al subdominio CENE, obteniendo un conocimiento bajo al obtener una puntuación media de las puntuaciones normadas de 41,6 sobre 100. Por otra parte, respecto a los contextos de enseñanza involucrados en los distintos ítems del cuestionario, el profesorado presenta mejores puntuaciones en el contexto de los juegos seguido de los recursos tecnológicos; en cambio, muestran más dificultades para contextualizar los problemas a partir de situaciones reales, al ser el contexto en el que obtienen menor porcentaje de respuestas correctas.

 

4.2. Estrategias metodológicas

 

Desde una perspectiva general, diversos autores señalan que la enseñanza de la estadística y, en consecuencia, el desarrollo de procedimientos y estrategias para resolver tareas estadísticas debe realizarse desde las primeras edades con el objetivo de alfabetizar estadísticamente al alumnado (e.g., Alsina, 2021; Batanero, 2013; Bryant y Nunes, 2012; Fryre et al., 2013; NCTM, 2003). Por consiguiente, es necesario reorientar la enseñanza de la estadística hacia una enseñanza que permita ofrecer oportunidades para que los estudiantes desarrollen, desde edades tempranas, la capacidad para interpretar y evaluar críticamente la información estadística, los argumentos apoyados en datos o los fenómenos estocásticos que las personas pueden encontrar en diversos contextos, incluyendo los medios de comunicación (Gal, 2002). Desde este marco, se propone como estrategia metodológica el diseño de tareas y, más concretamente, una situación de aprendizaje a partir del juego. El objetivo de la sesión es trabajar los contenidos estadísticos a partir de un torneo de Jenga (Figura 1).

 

Figura 1

Juego Jenga

La dinámica del juego consiste en ir moviendo bloques de la torre de la parte inferior a la parte superior sin que se caiga. Una vez eliminado un jugador, anota en la pizarra el número de resultados obtenidos, donde el ítem partida corresponde a los juegos realizados y movimientos al número de veces que ha conseguido coger una pieza sin tirar el bloque, quedando una tabla similar a la siguiente (Tabla 2):

 

Tabla 2

Recuento de datos

Partida	Movimientos
1	7
2	5
3	8

 

Ante esta situación, se pregunta al profesorado: a partir de la Jenga, ¿el juego sirve para trabajar la estadística?; en caso afirmativo, ¿qué conceptos y/o contenidos se pueden trabajar con relación a la enseñanza de la estadística?; ¿conoces un juego mejor?, ¿cuál?; ¿qué otras estrategias, a partir del juego, conoces para enseñar estadística?

A partir de estas preguntas iniciales, se les pide que piensen distintas estrategias y recursos para enseñar estadística con la finalidad que diseñen una tarea para, posteriormente, aplicarla en el aula con la supervisión de un formador. En este sentido, a partir del diálogo y la reflexión grupal, las preguntas anteriores pueden servir de guía para descubrir qué estrategias o soluciones son adecuadas para la enseñanza de la estadística.

Es importante destacar que, si basamos el aprendizaje de la estadística en actividades constructivas y lúdicas, puede ser una experiencia motivadora para el alumnado (Muñiz-Rodríguez et al., 2014). Por consiguiente, el profesorado no solo debe conocer el contenido estadístico que va a enseñar, sino también las distintas formas de implementar tareas para que el alumnado construya el conocimiento (Ribeiro et al., 2021).

 

5. CONOCIMIENTO DE LA PRÁCTICA MATEMÁTICA (KPM)

 

5.1. Descripción del subdominio y principales resultados

 

El Conocimiento de la Práctica Matemática (KPM), de acuerdo con Carrillo et al. (2018) hace referencia a los conocimientos del profesorado sobre las formas de crear o producir en matemáticas, considerando los aspectos de la comunicación matemática, el razonamiento y la prueba ligados a un tema matemático específico o general; es decir, consiste en saber qué es definir y cómo usar definiciones (Aguilar et al., 2013).

En Franco y Alsina (2022b), se caracteriza el KPM a la enseñanza de la estadística, denominándolo Conocimiento de la Práctica Estadística (CPE). Desde esta perspectiva, se focaliza en cómo se hace estadística, cómo se valida, se resuelven problemas, se comunican ideas estadísticas, etcétera. En este sentido, Wild y Pfannkuch (1999) ofrecen una perspectiva centrada en la resolución de problemas a partir del ciclo de investigación estadística: Problema (definir el problema); Plan (sistema de medición, diseño de muestreo, gestión de datos, análisis); Datos (recopilación, gestión y análisis de datos); Análisis (exploración de datos, análisis planificados y no planificados, generación de hipótesis); y, Conclusiones (interpretación, conclusiones, nuevas ideas). Desde esta perspectiva, a continuación, se describen algunas estrategias metodológicas para contribuir a la mejora de este conocimiento.

 

5.2. Estrategias metodológicas

 

Se presenta una propuesta enmarcada dentro de la metodología de Lesson Study, al ser un método de formación continua y de desarrollo profesional docente basado en la colaboración, siendo un factor clave en la mejora de la enseñanza de las matemáticas (Fernández y Yoshida, 2004). Esta metodología consiste en un proceso cíclico donde el profesorado trabaja en colaboración para, de acuerdo con Perry y Lewis (2009): a) Formular objetivos en colaboración para el aprendizaje y desarrollo a largo plazo de la población estudiantil; b) Planear una “lección n a investigar” diseñada para llevar a la práctica los objetivos; c) Implementar la lección gestionada por un miembro del equipo, reuniendo las evidencias sobre el aprendizaje y el desarrollo del estudiantado; y, d) Reflexionar y discutir sobre las evidencias reunidas durante la clase con la finalidad de mejorar la lección, la unidad de aprendizaje y la enseñanza.

Considerando que existen evidencias de la mejora de la formación docente a partir de esta metodología, como por ejemplo Fang y Lee (2010), que muestran la mejora significativa del desarrollo del conocimiento pedagógico del contenido, a continuación, se adapta la experiencia de Lesson Study llevada a cabo por Estrella et al. (2022) compuesta por ocho sesiones, orientada a la anticipación, acción y reflexión (Figura 2).

 

Figura 2

Modelo de Lesson Study de ocho sesiones (Estrella et al., 2022)

 

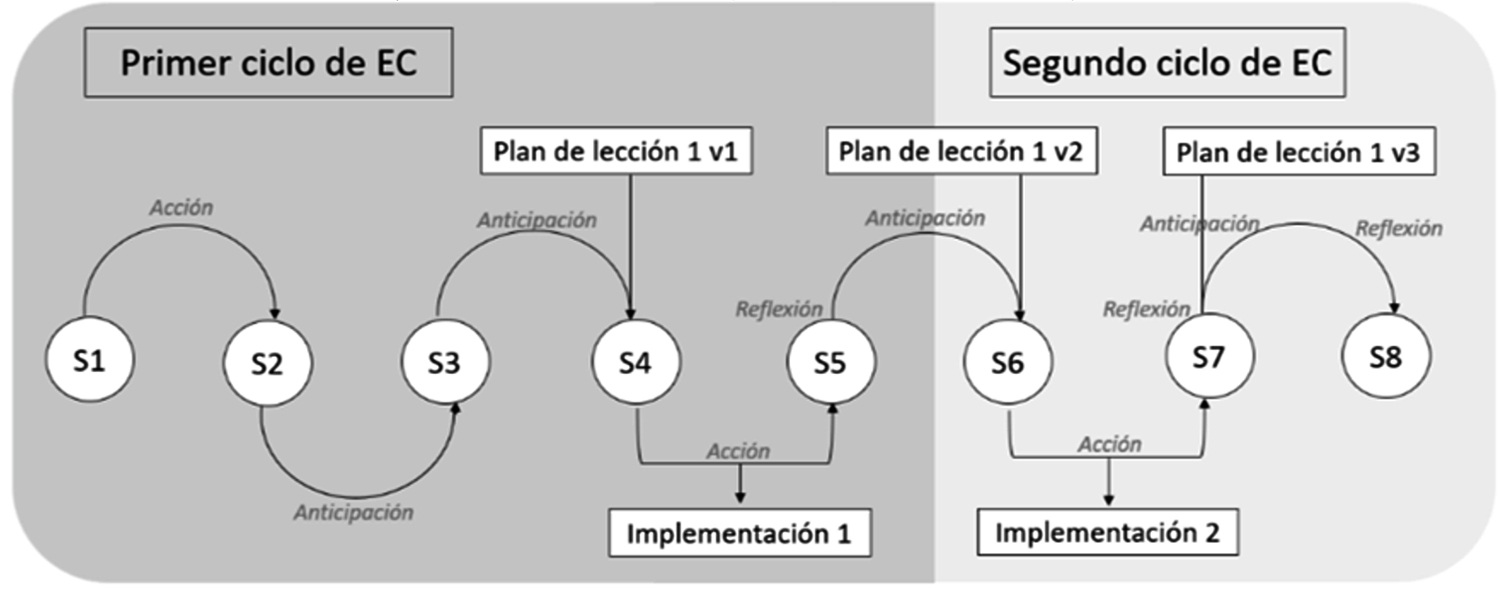
Como parte del proceso, el profesorado participante del curso de formación debe comenzar con la exploración y terminar con la presentación de sus productos a la clase. Se ponen en juego habilidades de modelación, que incluyen la capacidad para identificar preguntas relevantes, las relaciones en un contexto real, interpretar y dar solución al problema, entre otras. En otras palabras, durante las cuatro primeras sesiones se diseña un plan de acción situado en el enfoque de resolución de problemas; entre las sesiones 4 y 5 se implementa la primera versión del plan de la lección; en las sesiones 5 y 6 se sigue un proceso de mejora del plan de la lección para obtener una segunda versión mejorada entre las sesiones 6 y 7. En la sesión 7 se realiza una reformulación del plan anterior para alcanzar un plan de lección final. Finalmente, en la sesión 8 se finaliza con reflexiones acerca del proceso experimentado con el Lesson Study.

Siguiendo este modelo, se propone que los objetivos de aprendizaje correspondan a la representación y formalización del conocimiento estadístico a partir de representaciones de datos en estadística y la toma de decisiones en el análisis de datos en un caso asociado al Covid 19 que afectó a la población mundial en marzo del 2020. Por consiguiente, se presenta a los participantes una pirámide de población con los casos de COVID-19 confirmados en Galicia (España) hasta el 13 de agosto, ordenados por sexo y grupos de edad (Figura 3).

 

Figura 3

Pirámide población casos COVID-19

 

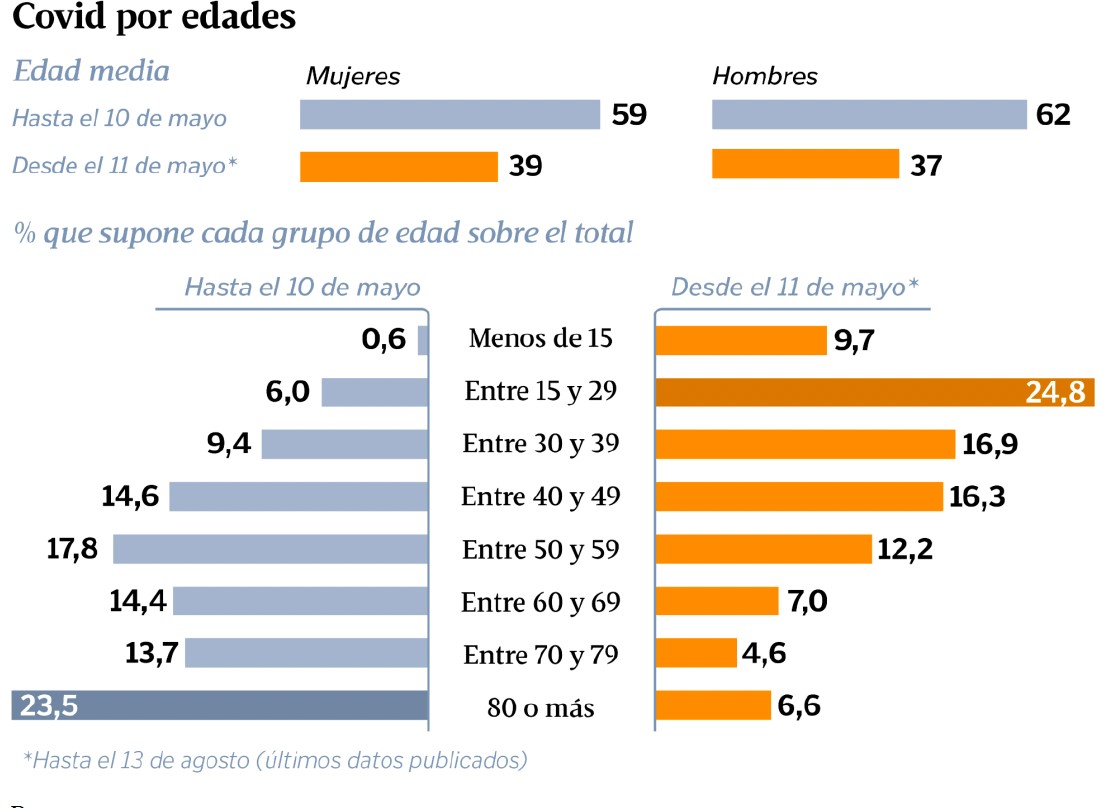
Posteriormente, después de dejar un espacio para la observación del gráfico y el posterior diálogo entre iguales, a partir de equipos cooperativos se pide que cada grupo elabore una situación de aprendizaje para, posteriormente, implementarla en una clase de educación primaria. Ante esta situación, los integrantes de los equipos cooperativos deben considerar distintas estrategias, realizar un diálogo y llegar a una conclusión para solucionar los posibles problemas del alumnado. Una vez diseñada e implementada la situación de aprendizaje, cada grupo debe analizar, consensuar y evaluar la práctica docente. Es importante destacar que, en muchas ocasiones, las creencias del profesorado determinan las decisiones que se toman durante el proceso de enseñanza-aprendizaje que se realiza en el aula (Olfos et al., 2015); por este motivo, es necesario disponer de situaciones colaborativas entre el profesorado para intercambiar opiniones y reflexiones acerca del profesorado experimentado y las distintas soluciones que se dan.

 

6. CONOCIMIENTO DE LAS CARACTERÍSTICAS DE APRENDIZAJE DE LAS MATEMÁTICAS (KFLM)

 

6.1. Descripción del subdominio y principales resultados

 

De acuerdo con Escudero y Carrillo (2014) este conocimiento hace referencia al conocimiento del profesorado sobre las características de aprendizaje inherentes a un determinado contenido matemático y al conocimiento de las teorías de aprendizaje de las matemáticas adquiridas a lo largo de la experiencia profesional desarrollando la construcción del conocimiento matemático. Además, según Carrillo et al. (2018), este subdominio incluye las características del proceso de comprensión de los estudiantes sobre los distintos contenidos matemáticos, considerando los errores, dificultades u obstáculos que el alumnado pueda tener en el proceso de enseñanza aprendizaje de las matemáticas. En otras palabras, se focaliza en las características de aprendizaje derivadas de la interacción del contenido matemático como objeto de aprendizaje, considerando el proceso de aprendizaje del alumnado como parte de este subdominio (Escudero y Carrillo, 2014; Sosa et al., 2013).

Desde este prisma, el Conocimiento de las Características de Aprendizaje de la Estadística (CCAE) requiere comprender los distintos contenidos y el lenguaje asociado a cada concepto estadístico, así como considerar los posibles errores o dificultades en el proceso de aprendizaje del alumnado (Franco y Alsina, 2022b). Por tanto, el profesorado debe conocer cómo el alumnado construye los significados desde los datos y qué tipos de representaciones producen cuando se enfrentan a una tarea basada en estos contenidos (Molina-Portillo et al., 2023). En definitiva, el profesorado debe dar significado estadístico a los comentarios y reflexiones del alumnado, aunque contenga errores, profundizando sobre el conocimiento estadístico (Ribeiro et al., 2021).

Los resultados del CCAE obtenidos en el estudio de Franco y Alsina (2024) muestran una dificultad muy pronunciada del profesorado para anticiparse a los posibles errores o dificultades que el alumnado puede llegar a presentar en su proceso de enseñanza-aprendizaje de la estadística, al obtener una puntuación media de las puntuaciones normadas de 27,07 sobre 100. Asimismo, respecto al papel que juegan los contextos de enseñanza en este tipo de conocimiento, el estudio revela que el profesorado tiene mayores dificultades en las situaciones donde se involucran los contextos reales, mientras que se desenvuelven algo mejor en las situaciones relacionadas con juegos y recursos gráficos.

 

6.2. Estrategias metodológicas

Para mejorar el CCAE del profesorado, se propone utilizar la estrategia metodológica Flipped Classroom en una situación de aprendizaje que se relacione con la estadística, al ser una metodología que da prioridad al autoaprendizaje, a la reflexión y proporciona una construcción activa del conocimiento (Andía et al., 2020). Además, de acuerdo con Tourón y Santiago (2015) la Flipped Classroom aporta los siguientes beneficios:

• Permite atender las diferencias individuales.

• El profesorado tiene la oportunidad de compartir información y conocimientos entre iguales, con el alumnado, con las familias y el resto de la comunidad educativa.

• El alumnado dispone de la posibilidad de acceder tantas veces como necesite a los contenidos facilitados por su profesorado.

• Aumenta las posibilidades del aprendizaje colaborativo.

• Favorece la autonomía y autorregulación del aprendizaje.

A continuación, a modo de ejemplo, se adapta la experiencia de formación propuesta por Sánchez-Cruzado y Sánchez-Compaña (2020).

En primer lugar, es necesario seleccionar qué contenidos se pretender trabajar: en nuestro caso, las medidas relacionadas con el análisis de datos y el pensamiento estadístico elemental. Desde esta perspectiva, se propone un trabajo en grupos reducidos que tienen como objetivo analizar las variables aleatorias cualitativas y cuantitativas de dos estudios estadísticos que sean de su interés (según las motivaciones y gustos del alumnado, se propone unas opciones u otras). Está actividad tiene como finalidad aprender los conceptos y contenidos estadísticos de forma práctica. Una vez elegido el tema, se crea un cuestionario, de forma conjunta y consensuada con todos los grupos, para obtener variables para los análisis estadísticos. Cada estudiante debe traer un mínimo de respuestas al cuestionario para, en la posterior sesión de clase, poner en común los datos, repartirlos y analizarlos en profundidad. Además, como trabajo individual, se proporciona al alumnado algunos vídeos teóricos sobre el aprendizaje de la estadística con el objetivo de dar herramientas y estrategias al alumnado para elaborar dichos análisis. Una vez en el aula, el alumnado tiene la posibilidad de preguntar dudas sobre conceptos y contenidos estadísticos que no entienda. En este sentido, el profesorado debe ser el guía en todo momento del aprendizaje del alumnado, observar y ver cómo aprenden y que dificultades obtienen en el proceso de aprendizaje. Es importante que el alumnado sea consciente que es un agente activo en ese proceso.

Al terminar la propuesta y, por tanto, el análisis del estudio del tema elegido, el docente, juntamente con el alumnado debe generar un debate sobre la importancia de la educación estadística, que errores, dificultades y obstáculos han tenido en su aprendizaje dando forma a sus vivencias durante el transcurso de la clase invertida.

Una vez finalizada la clase, a modo de sugerencia, el profesorado puede realizar un DAFO (Dificultades, Amenazas, Fortalezas y Oportunidades) del aprendizaje del alumnado, para ser consciente de como aprende el alumnado y, para posteriores ocasiones, tener estos aspectos en cuenta para realizar una enseñanza eficaz de la estadística.

 

7. CONOCIMIENTO DE LOS ESTÁNDARES DE APRENDIZAJE DE LAS MATEMÁTICAS (KMLS)

 

7.1. Descripción del subdominio y principales resultados

 

El Conocimiento de los Estándares de Aprendizaje de las Matemáticas (KMLS) hace referencia a los grados de profundidad de conocimiento del currículo de matemáticas junto con las indicaciones de asociaciones profesionales como el NCTM (2003) o las investigaciones científicas que tratan la materia (e.g., Carrillo et al., 2018; Muñoz-Catalán et al., 2015). En otras palabras, se refiere a los contenidos que el alumnado puede comprender en un curso escolar determinado y las informaciones provenientes de investigaciones (Aguilar et al., 2013). A modo de ejemplo, el Proyecto GAISE II (Bargagliotti et al., 2020) y los organismos NCTM (2003) y CCSSM (2012) incluyen las siguientes recomendaciones para desarrollar el pensamiento estadístico: 1) Entender qué comprende una pregunta estadística; 2) Saber cómo investigar preguntas estadísticas planteadas por profesores en un contexto de interés para jóvenes estudiantes; 3) Realizar un censo del aula para recoger datos y diseñar experimentos sencillos para comparar tratamientos; 4) Distinguir entre datos categóricos y numéricos; 5) Ordenar, clasificar y organizar datos; 6) Entender que los datos varían; 7) Entender el concepto de una distribución de datos y cómo describir características clave de esta distribución; 8) Comprender cómo representar distribuciones con tablas, imágenes, gráficos y resúmenes numéricos; 9) Comprender cómo comparar dos distribuciones; 10) Utilizar los datos para reconocer cuándo existe una asociación entre dos variables; 11) Comprender cómo inferir el análisis de los datos al aula desde la que se produjeron los datos y las limitaciones de este ámbito si queremos inferir más allá del aula.

Franco y Alsina (2022b) adaptan el KMLS a la enseñanza de la estadística dando lugar al Conocimiento de los Estándares de Aprendizaje de la Estadística (CEAE).

A partir de la investigación realizada por Franco y Alsina (2024) se deduce un conocimiento deficiente sobre el conocimiento de los estándares nacionales de aprendizaje de la estadística al obtener una puntuación media de las puntuaciones normadas de 33,87 sobre 100. Adicionalmente, el profesorado obtuvo las puntuaciones más bajas en los ítems relacionados con los recursos gráficos y las situaciones reales; en cambio, en similitud con otros subdominios, el profesorado se desenvuelve mejor en las situaciones que involucran los juegos y los recursos manipulativos.

 

7.2. Estrategias metodológicas

 

Considerando los datos indicados, se describe una actividad a partir de la metodología de la reflexión sobre la práctica, en la que a partir de un conjunto de buenas preguntas se pretende mejorar el CEAE del profesorado. Se opta por esta metodología ya que en distintos estudios previos se ha evidenciado su eficacia para mejorar la enseñanza de las matemáticas (e.g., Mabova et al., 2022; Pepin et al., 2017; Pourdavood y Yan, 2021)

A modo de ejemplo, una actividad que se puede realizar en la etapa de educación primaria (10-12 años) para enseñar contenidos estadísticos como la moda, la media, entre otros, es la siguiente: Se organiza la clase en grupos y se reparte un dado de seis caras (cada cara corresponde a un valor), una pizarra pequeña, y rotuladores. Cada componente del grupo realiza 10 tiradas y anota el resultado en una tabla (Tabla 3):

 

Tabla 3

Ejemplo de tabla para anotar los resultados

Resultados	Frecuencia
1	3
2	5
3	6
4	7
5	2
6	4

 

Una vez completada la tabla, el profesorado pide a cada grupo que realice un gráfico de barras con piezas de lego. A continuación, con el objetivo de analizar si existe un dominio del conocimiento sobre los conceptos relacionados con la estadística descriptiva, se abre un debate a partir de las siguientes preguntas:

• ¿Qué es la media?, ¿Cómo se calcula?

• ¿Se puede obtener una media aritmética para una variable nominal?, ¿Por qué?

• ¿Qué número se ha repetido más veces? Y, ¿el que menos?

• ¿Qué es la mediana?, ¿en qué situaciones se utiliza?

• ¿Cuál es la diferencia entre la media, la mediana y la moda?

• ¿Para qué nos sirve la moda?

• En el caso de lanzar dos dados de seis caras cada uno, ¿tendríamos los mismos resultados?, ¿por qué?

A través de este tipo de preguntas se busca promover el diálogo y, de esta forma, co-construir al concepto de media. Además, cabe destacar la importancia de diferenciar el concepto de media con el concepto de mediana, pues en muchos casos la confusión de estos conceptos lleva al error en un proceso de significación (Mayen et al., 2009)

A partir de este contexto, para promover el CEAE del profesorado, se propone debatir sobre las siguientes preguntas:

• ¿Qué conceptos y/o propiedades estadísticas deben usar los estudiantes para dar una solución correcta a este problema?

• ¿Qué intervenciones realizaría como docente para superar las dificultades del alumnado?

• ¿Con qué contenidos estadísticos podemos relacionar el contenido involucrado en este problema?

• A partir de la actividad anterior, ¿Cómo puede el profesorado evaluar el progreso del alumnado con relación a los estándares de aprendizaje?

• ¿Qué contenidos considera como mínimos para que el alumnado sea competente en estadística?

• ¿La actividad propuesta está acorde con el nivel de escolaridad del alumnado?

 

8. CONSIDERACIONES FINALES

 

En este artículo se han vinculado los resultados de una investigación previa sobre el conocimiento especializado del profesorado para enseñar estadística en educación primaria (Franco y Alsina, 2024) con diversas estrategias metodológicas asociadas al desarrollo profesional docente, con la finalidad de contribuir a la mejora de la práctica escolar.

Los resultados de dicha investigación han evidenciado importantes dificultades del profesorado en los distintos subdominios del MTSK (Carrillo et al., 2018) y en los distintos contextos de enseñanza involucrados: contextos reales, materiales manipulativos, juegos, recursos tecnológicos y recursos gráficos (Alsina, 2019, 2020).

Con el propósito de ayudar al profesorado de educación primaria a mejorar estos resultados, se han descrito distintas estrategias metodológicas para cada uno de los subdominios analizados:

• KoT/CTE: Este subdominio requiere conocer los contenidos estadísticos y sus significados fundamentados (Flores-Medrano et al., 2014) para enseñar estadística de manera eficaz. Para promover este subdominio de conocimiento, se ha descrito un juego de rol como estrategia metodológica: a partir de los distintos roles de cada participante en un hipotético programa de formación se ha impulsado la reflexión sobre contenidos de media, moda, mediana y variabilidad de datos, para tratar de promover una mejora en el sentido propuesto por Marimón et al. (2021).

• KSM/CEE: Este subdominio requiere conocer las distintas conexiones matemáticas y estadísticas para comprender y desarrollar conceptos más avanzados y obtener una mayor adquisición del contenido, abordando conexiones transversales a partir de una vinculación epistemológica de los conceptos (Aguilar et al., 2013; Muñoz-Catalán et al., 2015). Con la metodología de la reflexión de la práctica, se ha propuesto que el profesorado cuestione sus propias actividades y estrategias a partir de la destrucción, co-construcción y reconstrucción de conocimientos (Korthagen, 2001). Para ello, se han planteado una serie de preguntas para analizar las distintas conexiones que el profesorado pone en práctica en su proceso de enseñanza de la estadística.

• KMT/CENE: Este subdominio requiere conocer las distintas estrategias que el profesorado utiliza en el proceso de enseñanza-aprendizaje de la estadística como, por ejemplo, recursos materiales o visuales, conocimiento de estrategias de enseñanza y conocimiento de teorías personales o formales (Franco y Alsina, 2022b). Por consiguiente, se ha propuesto el diseño de tareas estadísticas a partir de una situación dada para que el profesorado piense distintas estrategias y recursos para enseñar estadística y las implemente en el aula con la supervisión de un formador.

• KPM/CPE: Este subdominio requiere conocer las distintas formas de crear o producir estadística, por ejemplo, en el marco de un ciclo de investigación estadístico (Wild and Pfannkuch, 1999). En este sentido, se ha propuesto la metodología Lesson Study (Fernández y Yoshida, 2004) para desarrollar conocimiento profesional sobre el proceso de enseñanza-aprendizaje de la representación y formalización del conocimiento estadístico a través de representaciones de datos y la toma de decisiones a partir de una pirámide de población de casos COVID-19. La finalidad de la actividad ha sido que los participantes consideren distintas estrategias para solucionar los posibles problemas del alumnado pues, como se ha argumentado con anterioridad, las creencias del profesorado pueden determinar las decisiones que se toman durante el proceso de enseñanza (Olfos et al., 2015).

• KFLM/CCAE: Este subdominio requiere conocer las características del proceso de comprensión de los estudiantes (Carrillo et al., 2018) considerando los distintos errores, dificultades u obstáculos que puedan tener durante el proceso de enseñanza-aprendizaje. Para mejorar este subdominio de conocimiento, se ha propuesto utilizar la metodología Flipped Classroom ya que, como se ha indicado, promueve el autoaprendizaje y proporciona una construcción activa del conocimiento (Andía et al., 2020).

• KMLS/CEAE: Este subdominio requiere conocer los distintos grados de profundidad del conocimiento del currículo. En este sentido, se han indicado recomendaciones de distintos organismos (e.g., CCSSM, 2015; NCTM, 2003) para desarrollar el pensamiento estadístico. Además, se ha descrito una actividad junto con el planteamiento de buenas preguntas para fomentar la mejora de este subdominio de conocimiento en un proceso formativo.

A modo de conclusión, pues, en este artículo se han ofrecido una variedad de estrategias metodológicas (Flipped Classroom, Lesson Study, reflexión de la práctica, creación de entorno de aprendizaje, entre otras) asociadas a cada uno de los subdominios de conocimiento del MTSK, con la finalidad de mejorar la enseñanza de la estadística. Cabe destacar que la selección de estas distintas estrategias se ha realizado con base en estudios preliminares que han evidenciado su eficacia en el desarrollo profesional docente, es decir, la adquisición por parte del profesorado de los conocimientos estadísticos, tanto didácticos como conceptuales, necesarios para desarrollar tareas que promuevan la alfabetización estadística en el alumnado de la etapa de educación primaria.

 

REFERENCIAS BIBLIOGRÁFICAS

Aguilar-González, Á., Carreño, E., Carrillo, J., Climent, N., Contreras, L. C., Escudero, D. I., Flores, E., Flores, P., Montes, M. y Rojas, N. (2013). El conocimiento especializado del profesor de matemáticas: MTSK. En CIBEM (Eds.), Actas del VII Congreso Iberoamericano de Educación Matemática (pp. 5063-5069). CIBEM.

Alsina, Á. (2018). Seis lecciones de educación matemática en tiempos de cambio. Itinerarios didácticos para aprender más y mejor. Padres y Maestros, 376, 13-20. https://doi.org/10.14422/pym.i376.y2018.002

Alsina, Á. (2019). Itinerarios didácticos para la enseñanza de las matemáticas (6-12 años). Graó. 

Alsina, Á. (2020). Enseñar estadística en Educación Primaria: primeras recomendaciones desde el Enfoque de los Itinerarios de Enseñanza de las Matemáticas En C. Ribeiro y A. Pavan (Eds.), Investigações hispanobrasileiras em Educação Estatística (pp. 107-112). Editora Akademy.

Alsina, Á. (2021). “Ça commence aujourd’hui”: alfabetización estadística y probabilística en la educación matemática infantil. PNA, 15(4), 243-266. https://doi.org/10.30827/pna.v15i4.21357

Alsina, Á., Vásquez, C., Muñiz-Rodríguez, L. y Rodríguez Muñiz, L. J. (2020). ¿Cómo promover la alfabetización estadística y probabilística en contexto? Estrategias y recursos a partir de la COVID-19 para Educación Primaria. Épsilon, 104, 99-128.

Andía, L. A., Santiago, R. y Sota, J. M. (2020). ¿Estamos técnicamente preparados para el flipped classroom? Un análisis de las competencias digitales de los profesores en España. Contextos Educativos. Revista de Educación, 25, 275-311. https://doi.org/10.18172/con.4218

Azcárate, P. y Cardeñoso, J. M. (2011). La Enseñanza de la Estadística a través de Escenarios: implicación en el desarrollo profesional. BOLEMA, Boletim de Educação Matemática, 24(40), 789-810.

Bakker, A., Cai, J y Zenger, L. (2021). Future themes of mathematics education research: an international survey before and during the pandemic. Educational Studies of Mathematics, 107(1), 1-24. https://doi.org/10.1007/s10649-021-10049-w

Ball, D., Thames, M.H. y Phelps, G. (2008). Content knowledge for teaching: What makes it special? Journal of Teacher Education, 59(5), 389-407. https://doi.org/10.1177/0022487108324554

Bargagliotti, A., Franklin, C., Arnold, P., Gould, R., Johnson, S., Perez, L. y Spangler, D. (2020). Pre-K-12 guidelines for assessment and instruction in statistics education II (GAISE II). American Statistical Association and National Council of Teachers of Mathematics.

Batanero, C. (2001). Didáctica de la Estadística. Grupo de Investigación en Educación Estadística.

Batanero, C. (2009). Retos para la formación estadística de los profesores. En J.A. Fernandes, F. Viseu, M.H. Martinho y P.F. Correia (Eds.), Actas do II Encontro de Probabilidade e Estatística_na_Scola (pp. 7-21). Universidade do Minho.

Batanero, C. (2013). La comprensión de la probabilidad en los niños. ¿Qué podemos aprender de la investigación? En J.A. Fernandes, P.F. Correia, M.H. Martinho y F. Viseu, (Eds.) Atas do III Encontro de Probabilidades e Estatítica na Escola (pp. 1-13). Universidade Do Minho.

Bryant, P. y Nunes, T. (2012). Children’s understanding of probability: A literature review. Nunffield Foundation.

Burrill, G. y Biehler, R. (2011). Fundamental statistical ideas in the school curriculum and in training teachers. En C. Batanero, G. Burrill y C. Reading (Eds.), Teaching statistics in school mathematics-Challenges for teaching and teacher education (p. 57-69). Springer. https://doi.org/10.1007/978-94-007-1131-0_10

Canal, Y. y Jaimes, É. (2013). Efectos de la simulación en la comprensión de la ley de los grandes números. Revista Integración, Temas de Matemáticas, 31(1), 69-86.

Carrillo, J., Climent, N., Montes, M., Contreras, L., Flores, E., Escudero, D. y Muñoz-Catalán, M. C. (2018). The mathematics teacher’s specialised knowledge (MTSK) model. Research in Mathematics Education, 20(3), 236-253. https://doi.org/10.1080/14794802.2018.1479981

Common Core State Standards for Mathematics [CCSSM] (2012). Common Core State Standards Initiative. CCSSO.

Escudero, D. y Carrillo, J. (2014). Knowledge of Features of Learning Mathematics as part of MTSK. En Proceedings PME, 306. PME

Estrella, S., Olfos, R. y Mena-Lorca, A. (2015). El conocimiento pedagógico del contenido de estadística en profesores de primaria. Educação e Pesquisa, 41(2), 477-493.
https://doi.org/10.1590/S151797022015041858

Estrella, S., Vidal-Szabó, P. y Morales, S. (2022). Enseñanza de la estadística en Chile con Lesson Study: innovaciones y buenas prácticas. En A. Salcedo y D. Díaz-Levicoy (Eds.), Formación del Profesorado para Enseñar Estadística: Retos y Oportunidades (pp.137-163). Centro de Investigación en Educación Matemática y Estadística.

Fang, Y. y Lee, C. (2010). Lesson Study and Instructional Improvement in Singapore. National Institution of Singapore.

Fernández, C. y Yoshida, M. (2004). Lesson study: A Japanese approach to improving mathematics teaching and learning. Routledge. https://doi.org/10.4324/9781410610867

Flores-Medrano, E., Escudero-Avila, D. I. y Aguilar-González, Á. (2013). Oportunidades que brindan algunos escenarios para mostrar evidencias del MTSK. En A. Berciano, G. Gutiérrez, A. Estepa y N. Climent (Eds.), Investigación en Educación Matemática XVII (pp. 275-282). SEIEM.

Flores-Medrano, E., Escudero-Ávila, D., Montes, M., Aguilar, A. y Carrillo, J. (2014). Nuestra modelación del conocimiento especializado del profesor de matemáticas, el MTSK. En J. Carrillo, L.C. Contreras, N. Climent, D. Escudero-Ávila, E. Flores-Medrano y M.A. Montes (Eds.), Un marco teórico para el conocimiento especializado del profesor de matemáticas (pp. 57-72). Universidad de Huelva.

Franco, J. y Alsina, Á. (2022a). El conocimiento del profesorado de Educación Primaria para enseñar estadística y probabilidad: una revisión sistemática. Aula Abierta, 51(1), 7-16. https://doi.org/10.17811/rifie.51

Franco, J. y Alsina, Á. (2022b). Conocimientos del profesorado para enseñar estadística y probabilidad. Educación Matemática, 34(3), 65-96. 

Franco, J. y Alsina, Á. (2023). Evaluando el conocimiento especializado para enseñar estadística y probabilidad: Elaboración y validación del Cuestionario MTSK-estocástico. Uniciencia, 37(1), 1-22. https://doi.org/10.15359/ru.37-1.5

Franco, J. y Alsina, Á. (2024). Specialized knowledge of in-service primary education teachers for teaching statistics. Manuscrito enviado para publicación.

Franklin, C. y Mewborn, D. (2006). The statistical education of PreK-12 teachers: A shared responsibility. En G. Burrill (Ed.), Thinking and reasoning with data and chance (pp. 335-344). NCTM.

Fryre, D., Baroody, A.J., Burchinal, M., Carver, S.M., Jordan, N.C. y McDowell, J. (2013). Teaching math to young children: A practice guide (NCEE 2014-4005). National Center for Education, Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education.

Gal, I. (2002). Adults’ statistical literacy: Meanings, components, responsibilities. International Statistical Review, 70(1), 1-25. https://doi.org/10.1111/j.1751-5823.2002.tb00336.x

Godino, J.D., Giacomone, B., Batanero, C. y Font, V. (2017). Enfoque ontosemiótico de los conocimientos y competencias del profesor de matemáticas. BOLEMA, Boletim de Educação Matemática, 31(57), 90-113. https://doi.org/10.1590/1980-4415v31n57a05

Koleza, E. y Kontogianni, A. (2012). Statistics in primary education in Greece: How ready are primary teachers? En D. Ben-Zvi y K. Makar (Eds.), The Teaching and Learning of Statistics (pp. 289-299). Springer. https://doi.org/10.1007/978-3-319-23470-0_34

Korthagen, F.A. (2001). Linking practice and theory. The pedagogy of realistic teacher education. Lawrence Erlbaum Associates.

Liñán, M.M., Contreras, L.C. y Barrera, V. (2016). Conocimiento de los Temas (KoT). En J. Carrillo, L.C. Contreras y M. Montes (Eds.), Reflexionando sobre el conocimiento del profesor. Actas de las II Jornadas del Seminario de Investigación de Didáctica de la Matemática de la Universidad de Huelva (pp.12 -20). SGSE.

Mabova, M.J., Jita, L.C. y Chimbi, G.T. (2022). Reaping the rewards of professional development: evidence from mathematics teachers’ pedagogical practices. International Journal of Instruction, 15(1), 873-890. https://doi.org/10.29333/iji.2022.15150a

Marimón, O., Diez-Palomar, J., Morales Maure, L. y Durán González, R. E. (2021). Evaluación de secuencias de aprendizaje de matemáticas usando la herramienta de los Criterios de Idoneidad Didáctica. Bolema: Boletim de Educação Matemática, 35, 1047-1072. https://doi.org/10.1590/1980-4415v35n70a23

Mayén, S., Díaz, C. y Batanero, C. (2009). Conflictos semióticos de estudiantes con el concepto de mediana. Statistics Education Research Journal, 8(2), 74-93.

Melief, K., Tigchelaar, A. y Korthagen, K. (2010). Aprender de la práctica. En O. Esteve, K. Melief y Á. Alsina (Eds.), Creando mi profesión. Una propuesta para el desarrollo profesional del profesorado (pp. 19-38). Octaedro.

Molina-Portillo, E., Contreras, J. M., Ruz, F. y Contreras, J. (2023). Transnumeration analysis linked to statistical literacy in prospective teachers. Profesorado, 27(1), 277-300. https://doi.org/10.30827/profesorado.v27i1.21488

Montes, M., Carrillo, J., Contreras, L. C., Liñán-García, M. M. y Barrera-Castarnado, V. J. (2019). Estructurando la formación inicial de profesores de matemáticas: una propuesta desde el modelo MTSK. En E. Badillo, N. Climent, C. Fernández y M. T. González (Eds.), Investigación sobre el profesor de matemáticas: formación, práctica de aula, conocimiento y competencia profesional (pp. 157-176). Ediciones Universidad Salamanca

Muñiz-Rodríguez, L., Alonso, P. y Rodríguez-Muñiz, L.J. (2014). El uso de los juegos como recurso didáctico para la enseñanza y el aprendizaje de las matemáticas: estudio de una experiencia innovadora. UNIÓN. Revista Iberoamericana de Educación Matemática, 39, 19-33.

Muñoz-Catalán, M. C., Contreras, L. C., Carrillo, J., Rojas, N., Montes, M. Á. y Climent, N. (2015). Conocimiento Especializado del Profesor de Matemáticas (MTSK): un modelo analítico para el estudio del conocimiento del profesor de matemáticas. La Gaceta de La Real Sociedad Matemática Española, 18(3), 1801-1817.

National Council of Teachers of Mathematics (2003). Principios y estándares para la educación matemática. Thales.

Olfos, R., Estrella, S. y Morales, S. (2015). Estudio de clases para la articulación de conocimientos en formación inicial. En R. Flores (Ed.), Acta Latinoamericana de Matemática Educativa, (pp. 1196-1202). Comité Latinoamericano de Matemática Educativa. 

Pepin, B., Xu, B., Trouche, L. y Wang, C. (2017). Developing a deeper understanding of mathematics teaching expertise: an examination of three Chinese mathematics teachers’ resource systems as windows into their work and expertise. Educational Studies in Mathematics, 94, 257-274. https://doi.org/10.1007/s10649-016-9727-2

Perry, R.R. y Lewis, C.C. (2009). What is successful adaptation of lesson study in the US? Journal of Educational Change, 10(4), 365-91. https://doi.org/10.1007/s10833-008-9069-7

Pourdavood, R. G. y Yan, M. (2021). Preparing Pre-service and In-service Teachers to teach mathematics and science using an integrated approach: the role of a six-week summer course. International Journal of Learning, Teaching and Educational Research, 20(1), 64-85. https://doi.org/10.26803/ijlter.20.1.4

Ribeiro, M., Almeida, A. y Mellone, M. (2021). Conceitualizando tarefas formativas para desenvolver as especificidades do conhecimento interpretativo e especializado do professor. Perspectivas da Educação Matemática, 14(35), 1-32. https://doi.org/10.46312/pem.v14i35.13263

Sánchez-Cruzado, C. y Sánchez-Compaña, M. T. (2020). El modelo flipped classroom, una forma de promover la autorregulación y la metacognición en el desarrollo de la educación estadística. Revista Interuniversitaria de Formación del Profesorado, 34(2), 121-142.

Shulman, L. (1987). Knowlendge and Teaching Fundations of the new reform. Harvard Educational Review, 52(1), 1-30.

Siswono, T. Y. E., Kohar, A. W. y Hartono, S. (2018). Designing Tasks to Examine Mathematical Knowledge for Teaching Statistics for Primary Teachers. Journal of Physics Conference Series, 947(1), 012008. https://doi.org/10.1088/1742-6596/947/1/012008

Sosa, L., Aguayo, L. M. y Huitrado, J. L. (2013). KFLM: Un entorno de aprendizaje para el profesor al analizar los errores de los estudiantes. En C. Dolores, M. S. García, J. A. Hernández, y L.Sosa (Eds.). Matemática Educativa: la formación de profesores (pp. 279-298). Díaz de Santos.

Tourón, J. y Santiago, R. (2015). El modelo Flipped Learning y el desarrollo del talento en la Escuela. Ministerio de Educación.

Vásquez, C. y Alsina, Á. (2022). Retos contemporáneos en la formación del profesorado: desarrollando competencias de sostenibilidad desde la educación estadística. Revista Científica Ecociencia, 9 (4), 111-132.

Vásquez, C. y Alsina, Á. (2015). El conocimiento del profesorado para enseñar probabilidad: Un análisis global desde el modelo del conocimiento didáctico-matemático. Avances de Investigación en Educación Matemática, 7, 27-48. https://doi.org/10.35763/aiem.v1i7.104

Vidal-Szabó, P. y Estrella, S. (2020). Extensión del modelo MTSK al dominio estadístico. En Y. Morales-López y A. Ruíz (Eds.), Educación Matemática en las américas 2019 (pp. 1036-1042). Comité Interamericano de Educación Matemática.

Watson, J.M., Callingham, R.A. y Donne, J.M. (2008). Establishing PCK for teaching statistics. En C. Batanero, G. Burrill, C. Reading y A. Rossman (Eds.), Joint ICMI/IASE Study: Teaching Mathematics Education. Challenges for Teaching and Teacher Education. Proceedings of the ICMI Study 18 (pp. 1-6). Springer

Watson, J. M. (1997). Assessing statistical thinking using the media. En I. Gal y J.B. Garfield (Eds.), The Assessment Challenge in Statistics Education (pp. 107-121) IOS Press and The International Statistical Institute.

Wild, C. y Pfannkuch, M. (1999). Statistical thinking in empirical enquiry. International Statistical Review, 67(3), 223-265. https://doi.org/10.1111/j.1751-5823.1999.tb00442.x

 

Como citar:

Seguí, J.F. y Alsina, Á. (2024). Estrategias metodológicas para mejorar el conocimiento especializado sobre la enseñanza de la estadística. Revista de Educación Estadística, 3, 1-25. https://doi.org/10.29035/redes.3.1.2

 

Esta obra está bajo una licencia de Creative Commons
Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional.

 

 

 

 

1. 1*Autor de correspondencia: joanfrancosegui@gmail.com (J.F. Seguí)

   https://orcid.org/0000-0002-4467-1469 (joanfrancosegui@gmail.com)

2. 2 https://orcid.org/0000-0001-8506-1838 (angel.alsina@udg.edu)