|
|
Revista de Educación Estadística Vol. 3, pp. 1-28, ene. 2024 - dic. 2024 ISSN 2810-6164 |
DOI: https://doi.org/10.29035/redes.3.1.1
RELACIÓN ENTRE LA CONSTRUCCIÓN DE ESPACIOS MUESTRALES Y EL RAZONAMIENTO PROPORCIONAL DE ESTUDIANTES COSTARRICENSES
Relação entre a construção de espaços amostrais e o raciocínio proporcional de estudantes da Costa Rica
Relating the construction of sample spaces and proportional reasoning in Costa Rican students
Luis A. Hernández-Solís1
Universidad Estatal a Distancia (Costa Rica)
Carmen Batanero2
Universidad de Granada (España)
María M. Gea3
Universidad de Granada (España)
Resumen
El objetivo del trabajo fue analizar la relación entre el nivel de razonamiento proporcional y la construcción del espacio muestral en estudiantes costarricenses. Para ello se utilizaron dos cuestionarios, cada uno con tres ítems de comparación de razones, que en conjunto consideran seis niveles diferentes de razonamiento proporcional. Además, los dos cuestionarios incluyeron dos ítems idénticos de construcción del espacio muestral compatible con un suceso seguro, equiprobable a su complementario e imposible. En las respuestas de 292 estudiantes de los cursos 6º a 10º (11-16 años) a estos cuestionarios se analiza el razonamiento proporcional mostrado y el tipo de suceso que tendría lugar según el espacio muestral construido. Los resultados indican que pocos estudiantes alcanzan el nivel más alto de razonamiento proporcional, aunque el porcentaje que lo consigue se incrementa con el curso. La construcción de espacios muestrales asociados a la obtención de un suceso imposible y seguro fue difícil y se observa una relación directa con el nivel de razonamiento proporcional, confirmada mediante la correlación entre el nivel de razonamiento proporcional y el número de espacios muestrales correctamente construidos.
Palabras clave: Probabilidad, Razonamiento, Evaluación.
Resumo
O objetivo do estudo foi analisar a relação entre o nível de raciocínio proporcional e a construção do espaço amostral em estudantes da Costa Rica. Para o efeito, foram utilizados dois questionários, cada um com três itens de comparação de razões, que no seu conjunto consideram seis níveis diferentes de raciocínio proporcional. Além disso, os dois questionários incluíam dois itens idênticos sobre a construção do espaço amostral compatível com um acontecimento certo, equiprovável ao seu complemento e impossível. As respostas de 292 alunos do 6º ao 10º ano (11 a 15 anos) a estes questionários analisam o raciocínio proporcional demonstrado e o tipo de acontecimento que ocorreria de acordo com o espaço de amostragem construído. Os resultados indicam que poucos alunos atingem o nível mais elevado de raciocínio proporcional, embora a proporção dos que o fazem aumente com o ano. A construção de espaços de amostra associados à realização de um acontecimento impossível e certo foi difícil e observa-se uma relação direta com o nível de raciocínio proporcional, confirmada pela correlação entre o nível de raciocínio proporcional e o número de espaços de amostra construídos corretamente.
Palavras-chave: Probabilidade, Raciocínio, Avaliação.
Abstract
The objective of this study was to analyze the relationship between the level of proportional reasoning and the construction of the sample space in Costa Rican students. For this purpose, two questionnaires were used, each with three ratio comparison items, which together consider six different levels of proportional reasoning. In addition, both questionnaires included two identical items on the construction of the sample space compatible with a certain, equiprobable to its complement and impossible event. In the responses of 292 students in grades 6-10 (11-15 years old) to these questionnaires we analyze the proportional reasoning shown and the type of event that would occur according to the constructed sample space. The results indicate that few students reach the highest level of proportional reasoning, although the proportion that reaches it increases with the course. The construction of sample spaces associated with the obtention of an impossible and certain event was difficult and a direct relationship with the level of proportional reasoning is observed, confirmed by the correlation between the level of proportional reasoning and the number of correctly constructed sample spaces.
Keywords: Probability, Reasoning, Assessment.
Recibido: 18/09/2023 - Aceptado: 16/11/2023
1. INTRODUCCIÓN
El espacio muestral (o conjunto de sucesos posibles del experimento aleatorio) es fundamental en el estudio de la probabilidad (Langrall y Mooney, 2005; Lima y Borba, 2021; Nunes et al., 2014), pues su composición se debe identificar para resolver cualquier problema probabilístico. En Costa Rica, se inicia su estudio en educación primaria (1º a 3º curso de Educación General Básica - EGB), al diferenciar situaciones aleatorias y seguras y clasificar los sucesos en más o menos probables. Conforme avanzan de curso, se continúa clasificando los sucesos en seguros, probables, equiprobables e imposibles y en 6º curso de EGB, analizan el espacio muestral para obtener la probabilidad de un suceso elemental. En 8º y 9º de EGB se retoman estos conceptos, y en 10º curso (Educación Diversificada, ED) se formalizan los axiomas básicos de probabilidades que se han venido trabajando en los años previos, introduciendo, además, la probabilidad de la unión de eventos (excluyentes y no excluyentes) y la probabilidad del complemento de un evento.
A pesar de su aparente sencillez, varias investigaciones (Chernoff, 2009; Chernoff y Zazkis, 2011; Hernández-Solís et al., 2021) informan de las dificultades del estudiantado con la identificación del espacio muestral, cuya construcción requiere del pensamiento multiplicativo y combinatorio (Zapata-Cardona, 2018), que se desarrolla lentamente, y se completa en la adolescencia (Batanero y Álvarez-Arroyo, 2023; Batanero et al., 1997; English, 2005). La asignación de probabilidades a los diferentes sucesos del espacio muestral, para determinar, por ejemplo, sucesos equiprobables, requiere igualmente del razonamiento proporcional, por lo que un nivel de razonamiento proporcional insuficiente podría dificultar la construcción y el trabajo con el espacio muestral.
El razonamiento proporcional ha recibido un gran interés en la investigación recogida, por ejemplo, en Ben-Chaim et al. (2012), Carpenter et al. (2012), Kieren (2020), Lamon (2007) o Van Dooren et al. (2018). El estudio del número racional se inicia en Costa Rica en la educación primaria, con el concepto de fracción, su lectura, escritura, representación gráfica, relación de orden, operaciones básicas, fracciones equivalentes y porcentajes. En 7º curso se trata la proporcionalidad inversa, en 8º el concepto de número racional y sus propiedades y en los siguientes cursos estos contenidos se aplican en la resolución de problemas (MEP, 2012).
En un trabajo previo (Batanero y Hernández-Solís, 2023) se llevó a cabo un estudio comparado del razonamiento proporcional en los cursos 6º a 9º de EGB y 10º de ED en Costa Rica y niveles escolares equivalentes en España. Por otro lado, Hernández-Solís et al. (2021) analizaron la construcción de espacio muestrales por una muestra estudiantes costarricenses de 6º curso de EGB. Sin embargo, no hemos encontrado estudios que analicen empíricamente la relación entre el razonamiento proporcional y la construcción del espacio muestral que corresponda a diversos tipos de sucesos en un experimento aleatorio. Para aportar información al respecto, en este trabajo analizamos la relación entre las respuestas a tareas de razonamiento proporcional y otras de construcción del espacio muestral por parte de los 292 estudiantes costarricenses de los cursos 6º a 10º que participaron en el estudio de Batanero y Hernández-Solís (2023).
La motivación para realizar el estudio es la relación entre la capacidad de construcción del espacio muestral, el razonamiento combinatorio (Batanero y Álvarez-Arroyo, 2023; Lockwood et al., 2020) y la resolución de problemas de probabilidad (Nunes et al., 2014; Langrall y Mooney, 2005), así como la existente entre la resolución de problemas de probabilidad y el razonamiento proporcional (Batanero y Hernández-Solís, 2023).
2. FUNDAMENTOS
El trabajo se basa en los niveles de razonamiento proporcional de Noelting (1980a; 1980b) y los antecedentes sobre comprensión del espacio muestral y lenguaje probabilístico, que se resumen a continuación.
2.1. Niveles de razonamiento proporcional de Noelting
Utilizaremos los niveles de Noelting (1980a; 1980b), quien analizó el razonamiento proporcional en problemas de comparación de mezclas de agua y zumo de naranja, según diferentes concentraciones: (a1, b1) y (a2, b2), donde el primer término de cada par (a) indica el número de vasos de zumo de limón y el segundo (b) el de vasos de agua en cada mezcla. Se ha elegido este tipo de problemas de comparación de razones, por estar muy relacionados con la comparación de probabilidades y por ser los utilizados por Noelting (1980a, 1980b) para describir los siguientes niveles de desarrollo del razonamiento proporcional:
• Nivel 0: Simbólico. Se resuelven los problemas en que solo hay que diferenciar los dos elementos en cada conjunto a comparar. Se resolverían problemas en que en una de las mezclas solo hubiese vasos de zumo de limón y en la otra únicamente vasos de agua.
• Nivel IA: Intuitivo inferior. Se solucionan los problemas en que los segundos términos de las fracciones (b1 y b2) son idénticos, comparando los primeros (a1 y a2). Es decir, cuando el número de vasos de agua es el mismo, basta comparar el número de vasos de zomo de limón. Un ejemplo, es el ítem 1 (Cuestionario A, Anexo).
• Nivel IB: Intuitivo medio. Se tiene éxito cuando los primeros términos de las fracciones (número de vasos de zomo de limón) son iguales (a1=a2), comparando los segundos (vasos de agua). Un ejemplo es el ítem 2 (Cuestionario B, Anexo).
• Nivel IC: Intuitivo superior. Se concibe la razón como un todo y se comparan las dos relaciones internas entre los términos de cada razón (a1<b1 y a2>b2; menos vasos de zumo que de agua en la primera mezcla y al contrario en la segunda) o entre ambas (a1<a2 y b1>b2; menos vasos de zumo en la primera mezcla y más vasos de agua en la segunda).
• Nivel IIA: Operacional concreta inferior. Se resuelven los problemas en los que los términos de cada razón son idénticos (clase de equivalencia de la unidad; a1/b1=a2/b2=1) es decir, igual número de vasos de zumo y de agua en cada mezcla. Estas relaciones deben tenerse en cuenta y se emplea la multiplicación o división. Un ejemplo es el ítem 3 (Cuestionario A, Anexo).
• Nivel IIB: Operacional concreta superior. Los problemas se caracterizan porque los términos de las dos razones entre vasos de zumo y de agua guardan la misma relación de proporcionalidad en cada mezcla (a1/b1 = a2/b2 = m/n); es decir, se presenta una clase de equivalencia diferente a la unidad. Un ejemplo es el ítem 4 (Cuestionario B, Anexo)
• Nivel IIIA: Operacional formal inferior. Dos de los cuatro términos de las razones son múltiplos, pero el resto no guarda la misma proporcionalidad. Surge una estrategia nueva, que combina multiplicación y suma. Por ejemplo, si m·a1=a2, y m·b1,>b2, entonces (a1, b1) < (a2, b2). Un ejemplo es el ítem 5 (Cuestionario A Anexo, en el que la relación de proporcionalidad entre vasos de zumo y de agua es diferente en cada mezcla)
• Nivel IIIB: Operacional concreta superior. Se resuelven problemas con fracciones cualesquiera, comparando dos razones equivalentes a las dadas en el problema, convirtiéndolas a denominador común. Un ejemplo sería el ítem 6 (Cuestionario B, Anexo).
La adquisición del razonamiento proporcional no se completa hasta el paso de las operaciones concretas a las operaciones formales (Butto et al., 2019; Lamon, 2007). Por otro lado, muchos estudiantes no resuelven las tareas que corresponden a su desarrollo lógico hasta varios años después (Van Dooren et al., 2018), incluso con instrucción (González-Forte, et al., 2022).
Otras investigaciones analizan el razonamiento proporcional de niños y niñas pequeños. Así, Boyer y Levine (2015) utilizaron problemas de mezcla similares a los del presente estudio, con niños y niñas de 8 y 10 años, quienes tuvieron mucha dificultad al tratar unidades discretas (vasos de zumo y de agua), mientras la mezcla es un continuo. Con 30 niños y niñas de 5 y 6 años, He et al. (2018) también emplearon problemas de mezclas, representándolas mediante rectángulos coloreados de la misma base y diferente altura. Concluyeron que algunos eran capaces de reconocer la proporcionalidad en fracciones equivalentes.
En Batanero y Hernández-Solís (2023) se comparó el nivel de razonamiento proporcional de estudiantes costarricenses y españoles entre 11 y 16 años (cursos 6º a 10º). Pocos alcanzaron el máximo nivel IIIB, ni siquiera en el curso 10º, y el razonamiento proporcional del estudiantado fue menor que el esperado para su edad en los estudios de Noelting (1980a; 1980b). Esta conclusión nos ha llevado a relacionar este nivel de razonamiento proporcional con diferentes tareas probabilísticas, en particular, con la construcción del espacio muestral, que se describe en este trabajo.
2.2. Compresión del espacio muestral
Aunque Piaget e Inhelder (1951) indicaron que a los 7 años ya pueden listar todos los resultados de un experimento aleatorio sencillo, otros autores indican que la falta de razonamiento combinatorio dificulta esta tarea (Lockwood et al., 2020). Jones et al. (1997) defendieron que el concepto de espacio muestral se desarrolla posteriormente al de probabilidad y describen una concepción incorrecta, consistente en no aceptar que todos los sucesos del espacio muestral podrían ocurrir.
Los y las estudiantes construyen espacios muestrales informales para justificar su solución a los problemas de probabilidad, por ejemplo, para indicar que todas las sumas de dos dados tienen la misma probabilidad (Speiser y Walter, 1998). Según Horvath y Lehrer (1998) su comprensión requiere las siguientes capacidades: a) reconocer todos los posibles resultados del experimento, b) describirlo en forma completa y c) relacionar el espacio muestral con la mayor o menor posibilidad de cada resultado del experimento. Langrall y Money (2005) proponen una escala de valoración de la comprensión de los estudiantes del espacio muestral. El nivel más bajo consiste en concentrarse simplemente en un suceso, por ejemplo, en la extracción de fichas de una urna, considerar sólo fichas del mismo color. En el segundo nivel se listan varios sucesos diferentes del espacio muestral, pero no todos; en el tercero se describe exhaustivamente todos los sucesos posibles y en el superior se listan de los elementos del espacio muestral de un experimento compuesto.
La clasificación de los casos como favorables o desfavorables para un cierto suceso es crucial para determinar su probabilidad. Sin embargo, Nilsson (2007) muestra que es complejo para los y las estudiantes, y algunos que listan todos los sucesos de un espacio muestral tienen dificultad al aplicar la regla de Laplace, porque no separan bien los casos favorables y desfavorables. Además, Chernoff y Zazkis (2011) y Konold (1989) indican que el estudiantado construye con frecuencia espacios muestrales no esperados por los profesores y que no siempre están de acuerdo con que los sucesos elementales del espacio muestral sean equiprobables, Ello explica algunos errores aparentes de probabilidad que se convierten en respuestas correctas, si se tiene en cuenta el espacio muestral personal construido por el o la estudiante (Chernoff, 2009).
Hernández-Solís et al. (2021) propusieron a 55 estudiantes costarricenses de 6º de educación básica construir el espacio muestral asociado a varios tipos de sucesos, en contextos de urnas y ruletas. Aunque fue sencillo construir un espacio muestral compatible con un suceso posible y equiprobable a su complementario, pocos lograron construirlo para los sucesos seguros (34,5% en ruletas y 29,1% en urnas) e imposible (25,5% en ruletas y 23,7% en urnas). Interesados por ver si esta dificultad persiste en cursos superiores, en este trabajo se propone una tarea similar a estudiantes de los cursos 6º a 10º junto con tareas de comparación de razones, para analizar la relación entre la construcción de espacios muestrales y el razonamiento proporcional.
2.3. Lenguaje de probabilidad
En las tareas de construcción del espacio muestral planteado en el cuestionario, se requiere comprender el significado de un suceso seguro, equiprobable e imposible, por lo que otro antecedente de este trabajo es la investigación sobre comprensión del lenguaje probabilístico.
Green (1983) analizó el significado que 3000 estudiantes ingleses de 11 a 16 años daban a los términos “puede ocurrir”, “igual posibilidad” e “imposible” y Cañizares (1997) replicó el estudio con 320 estudiantes españoles de 10 a 14 años. En ambos estudios la mayor dificultad fue comprender la idea de suceso seguro.
Hernández-Salmerón et al. (2017) analizaron el lenguaje del azar de 89 estudiantes de primer y segundo curso de educación secundaria en España (13-14 años), pidiéndoles escribir sinónimos de las palabras “imposible”, “posible”, “igual posibilidad”, “poca posibilidad”, “seguro”, “muy posible”. El porcentaje que no dio ningún sinónimo correcto para imposible fue de 48,2% en primer curso y de 33% en segundo y para seguro 73,2% en primer curso y 60,6% en segundo.
Groth et al. (2020) analizaron el lenguaje de probabilidad de 10 niños y niñas de 11 y 12 años, pidiéndoles situar algunas frases en una escalera de probabilidad, donde el imposible se situaba en el nivel más bajo y el seguro en el más alto. Los y las estudiantes tuvieron mayor dificultad para la expresión seguro que en la imposible y el lenguaje cualitativo no siempre precedió a la competencia cuantitativa de cálculo de probabilidades.
En todas estas investigaciones se pregunta por sinónimos de los términos probabilísticos, ordenarlos en una escala de probabilidad, o describir sucesos que sean probables, imposibles, seguros, etc. Este trabajo sigue una aproximación diferente, pues se presenta una tarea con el dibujo de un dispositivo aleatorio (ruletas o urnas) cuya composición se debe fijar para que ocurra un determinado suceso descrito mediante una expresión del lenguaje verbal probabilístico.
3. MÉTODO
3.1. Muestra
La muestra estuvo formada por 292 estudiantes de 6º a 9º de Educación General Básica (EGB) y 10º del Ciclo Diversificado (CD), con la composición descrita en la Tabla 1. Todos los estudiantes provenían de una escuela privada de la provincia de Cartago (Costa Rica) que incluye estudiantes de diferentes niveles económicos y sociales y es similar a muchos otros centros educativos en el país. Los datos se tomaron en mayo de 2022, con la autorización de la dirección del centro. Esta dirección informó que durante el año 2020, para afrontar posibles problemas causados por la COVID-19, se preparó material digital para los estudiantes que fueron atendidos a distancia para consultas. Al extenderse el problema de la pandemia, se retomó el horario normal de clases, impartidas en forma virtual. En 2021 se dieron clases bimodales, ya que mientras la mitad de cada clase asistía en forma presencial el resto seguía la clase virtualmente, lo cual se realizaba en semanas alternas, de modo que cada estudiante tuviese semanalmente la mitad de las clases presenciales. En 2022 las clases fueron totalmente presenciales. En general, se indica que en estos años se cumplió entre el 85% y 100% de los establecido por el Currículo nacional de Matemáticas.
Se trata de una muestra de conveniencia, elegida por su accesibilidad, proximidad geográfica, estar disponible en el momento del estudio y voluntad de participar. Este tipo de muestras se usan con frecuencia en la investigación educativa, lo cual es razonable cuando la composición de la población es relativamente homogénea y no se desea generalizar a toda la población (Etikan et al., 2016).
Tabla 1
Composición de la muestra, según curso escolar y cuestionario
|
Curso |
Edad (años) |
Cuestionario A |
Cuestionario B |
Total |
|
6º |
11-12 |
35 |
33 |
68 |
|
7º |
12-13 |
26 |
26 |
52 |
|
8º |
13-14 |
31 |
33 |
64 |
|
9º |
14-15 |
26 |
26 |
52 |
|
10º |
15-16 |
27 |
29 |
56 |
|
Total |
145 |
147 |
292 |
Nota: Elaboración propia
En cada uno de los grupos participantes (es decir, dos o tres grupos por cada curso escolar) se distribuyeron en forma aleatoria los cuestionarios A y B que se describen en la siguiente sección, a la mitad de los estudiantes. Esta técnica asegura la equivalencia de las muestras completas que pasaron los cuestionarios A y B, al dividirse la muestra total en forma aleatoria, dentro de cada grupo. Con ello se puede estimar el porcentaje de respuestas a cada ítem y categoría en la muestra total, partiendo de los datos de una de las submuestras y estimando una proporción similar en la segunda. Todo ello, debido a que se utilizan dos muestras equivalentes seleccionadas aleatoriamente de la muestra total y que la proporción muestral es el mejor estimador de la proporción poblacional.
3.2. Cuestionario
Cada estudiante completó uno de dos cuestionarios, A o B, cada uno con tres problemas de comparación de razones, de complejidad creciente, similares a los empleados por Boyer y Levine (2015), Noelting (1980a, 1980b), y Karplus et al. (1983). Entre los dos cuestionarios, que se presentan en el Anexo, se propusieron problemas de seis niveles diferentes de razonamiento proporcional según Noelting. Cada cuestionario se dio a la mitad de los y las estudiantes de cada curso, para tener aproximadamente igual número en cada curso respondiendo cada ítem. Con ello se quiso evitar la repetición de la respuesta al responder muchos ítems similares. En la Tabla 2 se especifican las características de cada ítem de razonamiento proporcional.
En estos ítems, se pide comparar dos razones (a1, b1) y (a2, b2), donde el primer término de cada par es el numerador (o dividendo) y el segundo el denominador (o divisor) de la razón vasos de zumo/vasos de agua. En el ítem 1 (cuestionario A), que compara las razones (2, 3) vs. (1, 3). Los otros cinco ítems tienen la misma estructura, variando el número de vasos de zumo y de agua.
Tabla 2
Ítems de razonamiento proporcional en los cuestionarios según nivel de Noelting (1980a; 1980b).
|
Ítem |
Cuestionario |
Composición |
Nivel de razonamiento proporcional de Noelting |
Edad esperada (años-meses) |
|
1 |
A |
(2, 3) vs (1, 3) |
IA. Intuitiva inferior |
(3-6) |
|
2 |
B |
(5, 1) vs (5, 4) |
IB. Intuitiva media |
(6-4) |
|
3 |
A |
(2, 2) vs (4, 4) |
IIA. Operacional concreta inferior |
(8-1) |
|
4 |
B |
(3, 1) vs (6, 2) |
IIB. Operacional concreta superior |
(10-5) |
|
5 |
A |
(3, 1) vs (4, 2) |
IIIA. Operacional formal inferior |
(12-2) |
|
6 |
B |
(3, 2) vs (4, 3) |
IIIB. Operacional formal superior |
(15-1) |
Nota: Elaboración propia
En los dos cuestionarios se añadieron los dos ítems 7 y 8 (ver Anexo) donde se pide construir un espacio muestral para que el suceso “gana María” sea, respectivamente, seguro, equiprobable a su complementario o imposible. Su resolución implica la comprensión del experimento aleatorio, y los sucesos implicados, según el apartado. Los ítems han sido tomados de Hernández-Solís et al. (2021), modificándose el ítem 7, cuyas ruletas estaban divididas en 4 partes y a cada una de estas partes se debía asignar numerales.
En el ítem 7 (ruletas), la probabilidad de los dos sucesos diferentes (blanco y negro) dependerá del número de sectores coloreados de cada color. Para que María gane con seguridad, todos los sectores de la ruleta deben colorearse en negro y todos en blanco para que sea imposible que María gane. La equiprobabilidad entre ganar y perder se logra coloreando la mitad del número de sectores de cada color. En el ítem 8 se debe formar un espacio muestral con cualquier número de fichas blancas y negras, siendo indistinguibles las del mismo color. Si todas las fichas son negras, se logra el suceso seguro (María gana), y si todas son blancas el imposible (María pierde). El suceso equiprobable a su complementario se logra si en la urna se representa el mismo número de fichas blancas y de fichas negras.
Se usan los dos contextos, discreto y continuo, porque la ruleta favorece las comparaciones de tipo parte-todo, mientras las urnas favorecen la comparación parte-parte (Cañizares, 1997). Además, en Hernández-Solís et al. (2021) fue más sencillo el contexto de ruletas.
3.3. Categorías de análisis
A continuación, se describen las categorías usadas para clasificar las respuestas de los estudiantes, comenzando por la comparación de razones y, seguidamente, la construcción de espacios muestrales.
Comparación de razones
• Comparar los totales, es decir, el número de vasos (zumo de limón y agua) en cada mezcla. Es siempre incorrecta, aunque da una respuesta correcta para el ítem 1.
S6: Sabe más el de Elena porque le puso mayor cantidad (ítem 1: (2, 3) vs (1, 3)).
• Comparar los primeros términos de la razón. Sólo proporciona resultados correctos cuando los segundos son iguales (b1 = b2). Corresponde al nivel intuitivo inferior (IA) de Noelting (1980a, 1980b) y proporciona respuestas correctas al ítem 1.
S6: Sabe más el de Elena porque le puso más limón (ítem 1: (2, 3) vs (1, 3)).
• Comparar los segundos términos cuando coinciden los primeros términos en la razón (a1 = a2). Corresponde al nivel intuitivo intermedio (IB) de Noelting (1980a, 1980b). Da respuestas correctas al ítem 2.
S172: Tiene menor cantidad de agua (ítem 2: (5, 1) vs (5, 4)).
• Comparar las diferencias entre los términos de cada razón. Esta estrategia es típica del nivel intuitivo superior (IC) y válida en los ítems 1 y 2
S35: Misma cantidad de agua pero la de Elena tiene más limón (ítem 1: (2, 3) vs (1, 3))
• Relación de equivalencia a la unidad. Se compara una razón (a1, b1) con la otra (a2, b2), aplicando una operación multiplicativa a sus términos, y descubriendo la equivalencia a la unidad. Corresponde al nivel operativo concreto inferior (IIA) de Noelting (1980a; 1980b) y resuelve el ítem 3.
E69: Los dos iguales, porque tienen la misma cantidad de zumo y agua (ítem 3: (2, 2) vs (4, 4)).
• Relación de equivalencia entre razones. Se compara una razón con la otra mediante una operación multiplicativa, comprobando que son equivalentes. Corresponde al nivel operativo concreto superior IIB de Noelting (1980a; 1980b) y da respuestas correctas en el ítem 4.
E156: Lo mismo, porque la cantidad de limonada de Elena es más pequeña y también la de agua, como si la de Juan se hubiese multiplicado por 2 (ítem 4: (3, 1) vs (6, 2)).
• Correspondencia entre los términos de las razones. Se establece una proporcionalidad entre los términos de una razón (a1, b1) para determinar si la relación en la otra (a2, b2) es menor o mayor. Corresponde al nivel operativo formal inferior (IIIA), y resuelve correctamente el ítem 5.
E109: La primera se concentra en menos agua. Por cada vaso hay tres vasos de limón, así que Juan debe usar seis vasos de limón para que sea tan ácido como del de Elena (ítem 5: (3, 1) vs (4, 2)).
• Proporcionalidad. Se reducen las razones a fracciones de denominador común para compararlas y da respuestas correctas a cualquier ítem de comparación de razones. Corresponde al nivel IIIB operativo formal superior de Noelting (1980a; 1980b).
E80: Porque el porcentaje de limón de Elena (60%) es mayor que el de Juan (57%) (ítem 6: (3, 2) vs (4, 3)).
Construcción del espacio muestral
La respuesta proporcionada para cada apartado en los ítems 7 y 8 se codificó como correcta o incorrecta, y dentro de éstas se diferenció el tipo de suceso implicado en el espacio muestral construido, siguiendo los criterios utilizados en Hernández-Solís et al. (2021):
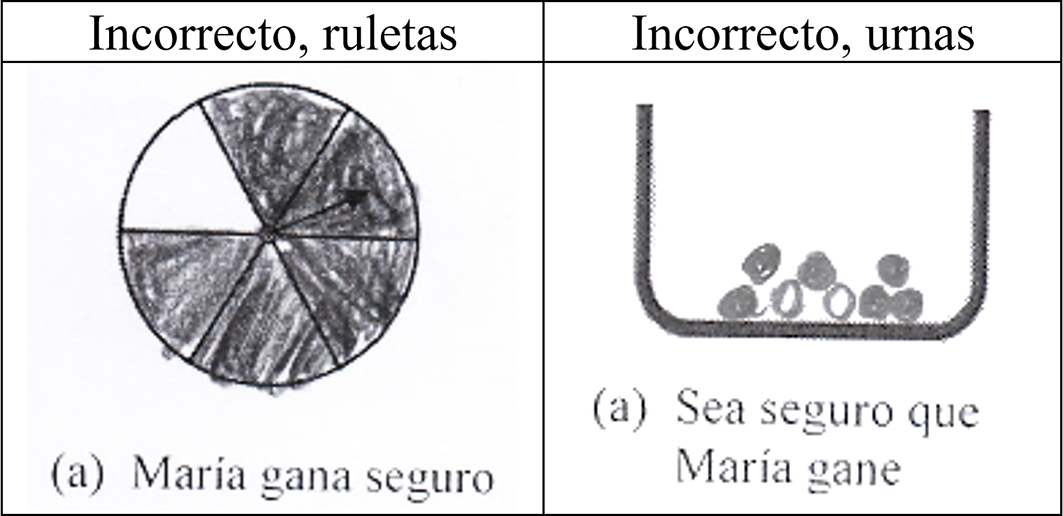
Espacio muestral que proporciona un suceso seguro: Se consideró que la respuesta es correcta si el estudiante construye un espacio muestral formado sólo por casos favorables al suceso “María gana seguro”. En la Figura 1 se muestran algunos ejemplos incorrectos. En el primero (ruletas), la probabilidad de ganar María sería 5/6; es decir, se confunde el suceso “seguro” con el suceso “muy probable”. En el ejemplo incorrecto para el contexto de urnas, se construye también un espacio muestral para el suceso “muy probable que María gane” con probabilidad 6/8. En los dos ejemplos, aunque el número de casos favorables es grande, se incluye también algún caso desfavorable.
Figura 1
Espacios muestrales incorrectos para el suceso seguro
Nota. Elaboración propia
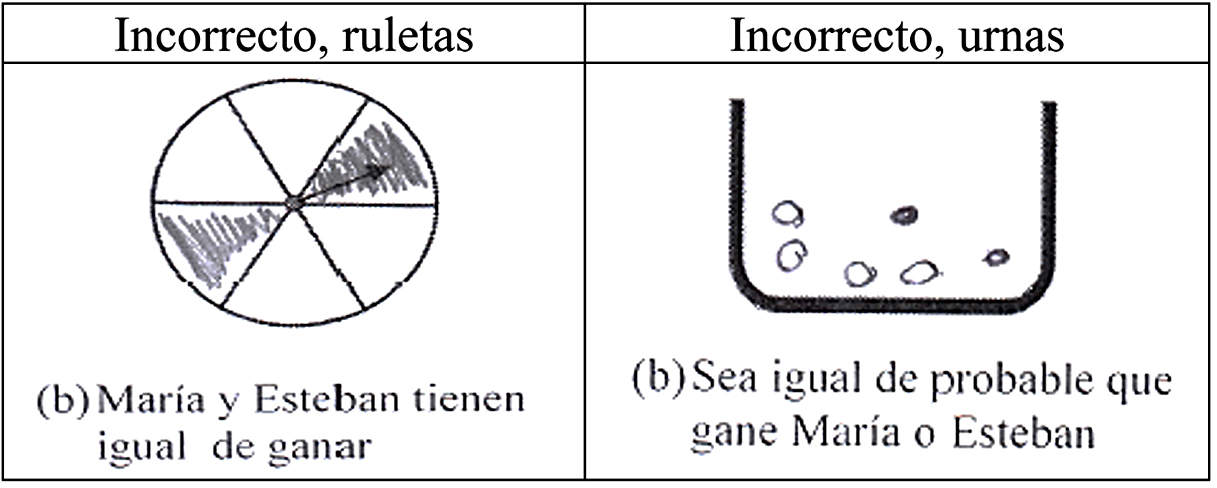
Espacio muestral que proporciona un suceso equiprobable a su complementario. El segundo apartado de los ítems 7 y 8 solicita al estudiante construir un espacio muestral tal que los sucesos “María gana” y “María pierda” sean equiprobables. La respuesta se ha considerado correcta si el estudiante incluye en el espacio muestra el mismo número de casos favorables y desfavorables. En la Figura 2 se presentan algunas respuestas incorrectas, con dos casos favorables y cuatro desfavorables. En el primero, se unen sectores blancos adjuntos como un solo suceso elemental; así el estudiante considera que hay dos casos favorables y dos casos desfavorables. En el segundo se mostraría el sesgo de equiprobabilidad (Lecoutre, 1992), al considerar equiprobable cualquier resultado de un experimento aleatorio, independientemente del número de casos favorables y posibles.
Figura 2
Espacios muestrales incorrectos para el suceso equiprobable a su complementario
Nota. Elaboración propia
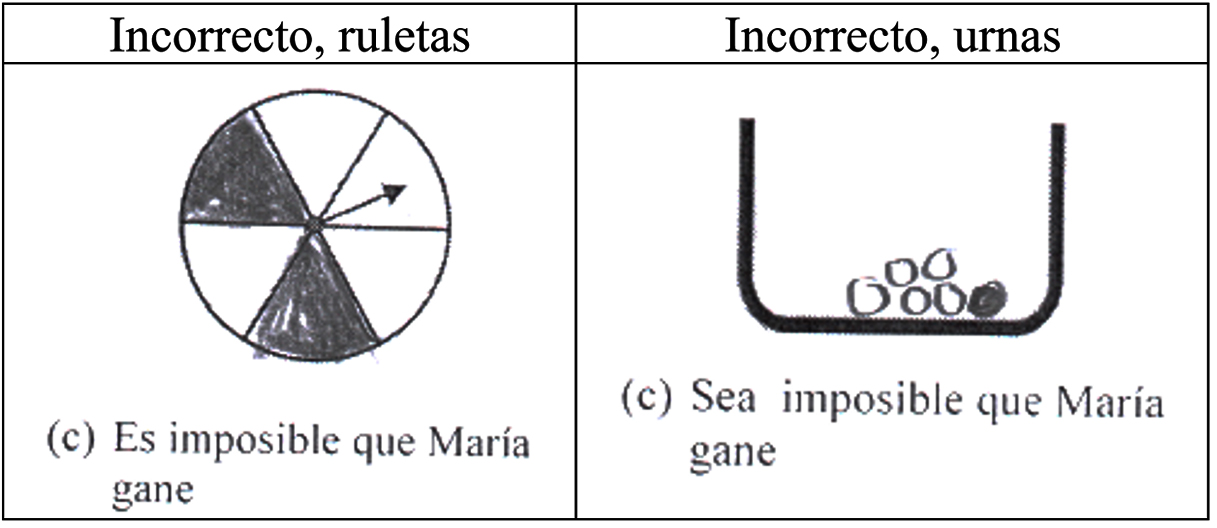
Espacio muestral que corresponde a un suceso imposible. El último apartado de ambos ítems consiste en determinar un espacio muestral que haga imposible que María gane el juego, para lo cual, el espacio muestral ha de estar compuesto totalmente por sucesos desfavorables. Se presentan en la Figura 3, ejemplos incorrectos que evidencian confusión entre los sucesos probable (primer ejemplo) o muy poco probable (segundo ejemplo) e imposible-
Figura 3
Espacios muestrales incorrectos para el suceso imposible
Nota. Elaboración propia
4. RESULTADOS
A continuación, se presenta el nivel de razonamiento proporcional alcanzado por el estudiantado de la muestra, seguido por los resultados obtenidos en la construcción del espacio muestral en contexto de ruletas y de urnas, para finalizar con el análisis de su relación.
4.1. Nivel de razonamiento proporcional
En la Tabla 3 se presenta el porcentaje de estudiantes que en cada curso se sitúan en cada nivel de razonamiento proporcional de Noelting (1980a, 1980b). Para determinar el nivel de un o una estudiante se ha comprobado que ha resuelto el problema correspondiente a dicho nivel utilizando una estrategia correcta y no logra resolver problemas de nivel superior de los contenidos en su cuestionario.
Pocos estudiantes alcanzaron los niveles IIB y superiores, ni siquiera en el último curso, de lo que deducimos que la edad supuesta por Noelting para lograr estos niveles no se cumple en la muestra del estudio, confirmando lo expuesto en González-Forte et al. (2022) y Van Dooren et al. (2018). No obstante, se observa un crecimiento generalizado del nivel de razonamiento proporcional con el curso escolar. Así, el porcentaje de estudiantes en los niveles IIB y superiores va creciendo con el curso, mientras que los niveles inferiores disminuyen con el curso.
Tabla 3
Porcentaje de estudiantes que alcanzan los diferentes niveles de razonamiento proporcional por curso
|
Nivel de razonamiento proporcional |
Curso |
||||
|
6º |
7º |
8º |
9º |
100 |
|
|
0 |
11,8 |
11,5 |
14,1 |
13,5 |
10,7 |
|
IA |
11,8 |
11,5 |
12,5 |
5,8 |
10,7 |
|
IB |
30,9 |
26,9 |
21,9 |
23,1 |
17,9 |
|
IIA |
29,4 |
25,0 |
21,9 |
23,1 |
19,6 |
|
IIB |
13,2 |
17,3 |
18,8 |
17,3 |
21,4 |
|
IIIA |
2,9 |
5,8 |
9,4 |
13,5 |
14,3 |
|
IIIB |
1,9 |
1,6 |
3,8 |
5,4 |
|
Nota. Elaboración propia
4.2. Espacios muestrales construidos en contexto de ruletas
En la Tabla 4 se presenta el porcentaje que en cada curso construye un espacio muestral correcto para cada tipo de suceso (seguro, equiprobable e imposible), en contexto de ruletas.
Tabla 4
Porcentaje de estudiantes que construyen correctamente el espacio muestral en contexto de ruletas, por curso
|
Suceso pedido |
|||
|
Curso |
Suceso seguro |
Suceso equiprobable a su complementario |
Suceso imposible |
|
6º |
25,0 |
88,2 |
36,8 |
|
7º |
55,8 |
90,4 |
65,4 |
|
8º |
34,4 |
87,5 |
48,4 |
|
9º |
51,9 |
80,8 |
57,7 |
|
10º |
41,1 |
91,1 |
46,4 |
Nota. Elaboración propia
Se observa que fue mucho más sencillo construir el espacio muestral que lleva a un suceso equiprobable a su complementario en el juego propuesto, pues casi el 90% en todos los cursos lo construye correctamente, no observándose un patrón regular de mejora de las respuestas con el curso escolar en los otros tipos de sucesos. El porcentaje del estudiantado de 6º curso que resuelven adecuadamente la pregunta sobre el suceso seguro es algo menor que el obtenido en Hernández-Solís et al. (2021) (34,5%) y mayor para el suceso imposible que en su estudio (25,5%). En la Tabla 5 se clasifican las respuestas, según el suceso a que da lugar el espacio muestral construido, resaltando con negrita las correctas.
Tabla 5
Porcentaje de espacios muestrales construidos en contexto de ruletas
|
Suceso pedido |
|||
|
Espacio muestral construido |
Suceso seguro |
Suceso equiprobable a su complementario |
Suceso imposible |
|
Suceso seguro |
40,4 |
0,3 |
1,7 |
|
Suceso muy probable |
37,7 |
0,7 |
1,7 |
|
Suceso equiprobable a su complementario |
5,1 |
87,7 |
1,7 |
|
Suceso posible |
7,9 |
3,4 |
9,2 |
|
Suceso poco probable |
2,7 |
2,1 |
29,5 |
|
Suceso imposible |
0,7 |
0,7 |
50,0 |
|
Construcción confusa |
0,3 |
||
|
No responde |
5,5 |
4,8 |
6,2 |
Nota. Elaboración propia
Los principales errores (Tabla 5) fueron confundir los sucesos “seguro” con “muy probable” o “imposible” con “poco probable”, coincidiendo con Cañizares (1997), Green (1983), Groth (2020), Hernández-Salmerón et al. (2017) y Hernández-Solís et al. (2021).
4.3. Espacios muestrales construidos en contexto de urnas
En la Tabla 6 se presenta el porcentaje de estudiantes que construye un espacio muestral correcto para cada tipo de suceso en contexto de urnas, por curso; y en la Tabla 7, se clasifican las respuestas por espacio muestral construido, resaltando en negrita las correctas.
Al comparar con los trabajos sobre comprensión del lenguaje de probabilidad, encontramos que Green (1983) obtuvo 18%, 25% y 34% para “igual posibilidad” y 84%, 84% y 89% para “imposible” en los cursos 6º, 7º y 8º, respectivamente. Por su parte, Cañizares (1997) obtuvo 42,9%, 52,9% y 57,5% para “igual posibilidad” y 81,3%, 83,9% y 78,1% para “imposible” en los mismos niveles educativos.
Tabla 6
Porcentaje de estudiantes que construyen correctamente el espacio muestral en contexto de urnas, por curso
|
Curso |
Suceso seguro |
Suceso equiprobable con su complementario |
Suceso imposible |
|
6º |
22,1 |
89,7 |
33,8 |
|
7º |
50,0 |
92,3 |
67,3 |
|
8º |
35,9 |
87,5 |
51,6 |
|
9º |
44,2 |
84,6 |
55,8 |
|
10º |
41,1 |
89,3 |
48,2 |
Nota. Elaboración propia
Tabla 7
Porcentaje de espacios muestrales construidos en contexto de urnas
|
Suceso pedido |
|||
|
Espacio muestral construido |
Suceso seguro |
Suceso equiprobable con su complementario |
Suceso imposible |
|
Suceso seguro |
37,7 |
3,1 |
|
|
Suceso muy probable |
42,1 |
0,3 |
2,1 |
|
Suceso equiprobable a su complementario |
0,7 |
88,7 |
0,3 |
|
Suceso posible |
7,5 |
3,4 |
5,1 |
|
Suceso poco probable |
2,7 |
0,7 |
32,9 |
|
Suceso imposible |
2,7 |
0,4 |
50,3 |
|
Construcción confusa |
0,4 |
||
|
No responde |
6,2 |
6,5 |
6,2 |
Nota. Elaboración propia
Considerando los resultados expuestos en las tablas 6 y 7, no aparecen grandes diferencias con el contexto de urnas. En los dos ítems, los resultados son inferiores que los de las investigaciones antes mencionadas; pero hay que señalar que la tarea propuesta en esta investigación es más compleja, puesto que se pide, además de comprender el lenguaje de probabilidad, construir el espacio muestral. Por otro lado, no se observa tan claramente el progreso en la tarea respecto al curso escolar, como en las citadas investigaciones; pareciera, que, sin importar el curso escolar, el nivel de complejidad de la tarea se mantiene constante para el estudiantado. Se conjetura que el bajo porcentaje de respuestas correctas puede deberse a que este tipo de tareas no son comunes en las lecciones de probabilidad costarricense.
4.4. Relación entre la construcción de espacios muestrales y el nivel de razonamiento proporcional
En la Tabla 8 se presenta el porcentaje del estudiantado que construye un espacio muestral correcto para cada tipo de suceso (seguro, equiprobable a su complementario e imposible), tanto en contexto de ruletas como de urnas, según el nivel de razonamiento proporcional observado en la comparación de razones. Se aprecia un crecimiento de las respuestas correctas, prácticamente en los tres tipos de sucesos y los dos contextos en función del nivel de razonamiento proporcional, mientras este crecimiento no era visible en relación al curso (Tablas 4 y 6). En particular, mientras el porcentaje global de construcciones correctas para los sucesos seguro e imposible era inferior o igual al 40% hasta llegar al nivel IIA, es cercano al 80% en el nivel IIIA y supera el 85% en el nivel IIIB.
Para analizar la posible significación estadística de estos resultados, en las Tablas 9 y 10 se presentan las medidas de correlación no paramétricas Tau de Kendall y Rho de Spearman entre el curso, nivel de razonamiento proporcional y número de respuestas correctas para la construcción de espacios muestrales en contexto de ruletas y urnas, así como para el suceso seguro, equiprobable e imposible y número total de espacios muestrales construidos, resaltando en negrita los resultados estadísticamente muy significativos. Se utilizan medidas no paramétricas debido a que las variables curso y nivel de razonamiento proporcional son ordinales.
Tabla 8
Porcentaje de estudiantes que construyen correctamente el espacio muestral en contexto de ruletas y urnas por nivel de razonamiento proporcional
|
Nivel de razonamiento proporcional |
Suceso pedido |
|||||
|
Suceso seguro |
Suceso equiprobable a su complementario |
Suceso imposible |
||||
|
Ruleta |
Urna |
Ruleta |
Urna |
Ruleta |
Urna |
|
|
0 |
38,5 |
15,4 |
74,4 |
69,2 |
46,2 |
35,9 |
|
IA |
19,4 |
25,8 |
83,9 |
87,1 |
38,7 |
45,2 |
|
IB |
19,7 |
22,5 |
84,5 |
91,5 |
35,2 |
36,6 |
|
IIA |
40,3 |
38,8 |
92,5 |
94,0 |
47,8 |
49,3 |
|
IIB |
56,9 |
58,8 |
94,1 |
90,2 |
66,7 |
66,7 |
|
IIIA |
80,8 |
69,2 |
96,2 |
96,2 |
73,1 |
76,9 |
|
IIIB |
85,7 |
85,7 |
85,7 |
85,7 |
85,7 |
85,7 |
Nota. Elaboración propia
Tabla 9
Correlaciones no paramétricas (Tau de Kendall) entre el número de espacios muestrales correctos, nivel de razonamiento proporcional y curso escolar.
|
Curso |
p |
Nivel razonamiento proporcional |
p |
|
|
Curso |
,097* |
.037 |
||
|
Ruletas |
,058 |
,238 |
,269** |
.000 |
|
Urnas |
,068 |
.162 |
,310** |
.000 |
|
Suceso seguro |
,097 |
,056 |
,300** |
,000 |
|
Suceso equiprobable a su complementario |
-0,012 |
,818 |
,185** |
,000 |
|
Suceso imposible |
,055 |
,278 |
,221** |
,000 |
|
Total espacios correctos |
,065 |
,169 |
.292** |
,000 |
Nota. Elaboración propia
Tabla 10
Correlaciones no paramétricas (Rho de Spearman) entre el número de espacios muestrales correctos, nivel de razonamiento proporcional y curso escolar.
|
Curso |
p |
Nivel razonamiento proporcional |
p |
|
|
Curso |
,122* |
.037 |
||
|
Ruletas |
,070 |
,230 |
,324 |
,000 |
|
Urnas |
,079 |
,178 |
,360 |
,000 |
|
Suceso seguro |
,112 |
,055 |
,358 |
,000 |
|
Suceso equiprobable a su complementario |
-0,14 |
,818 |
,212 |
,000 |
|
Suceso imposible |
,064 |
,275 |
,262 |
,000 |
|
Total espacios correctos |
,079 |
,175 |
,362 |
,000 |
Observamos en las dos tablas correlaciones estadísticamente muy significativas entre el nivel de razonamiento proporcional y cada una de las variables citadas, excepto para el curso, que no presenta correlaciones estadísticamente significativas con las variables relacionadas con la construcción del espacio muestral, aunque si hay una pequeña correlación significativa con el curso escolar. Aunque las correlaciones tienen un tamaño pequeño o moderado, son de sentido positivo, lo que muestra una asociación directa entre el nivel de razonamiento proporcional y la construcción de espacios muestrales de cada uno de los tipos estudiados en el trabajo.
4. DISCUSIÓN Y CONCLUSIONES
En este trabajo se ha analizado la construcción que realizan un grupo de estudiantes costarricenses de espacios muestrales asociados a sucesos seguros, equiprobable a su complementario e imposibles. Los resultados muestran la confusión que tienen estos y estas estudiantes entre suceso seguro y muy probable, que también apareció en las investigaciones de Cañizares (1997), Green (1983), Hernández-Salmerón et al. (2017) y Hernández-Solís et al. (2021). Es también generalizada la identificación de sucesos muy poco probables e imposible, también citada por Cañizares (1997), Green (1983), Hernández-Salmerón et al. (2017) y Hernández-Solís et al. (2021). Respecto al suceso equiprobable a su complementario, algunos de los ejemplos analizados indican la posibilidad de que se considere solo el color de resultado, sin tener en cuenta su probabilidad, coincidiendo con lo expuesto por Chernoff y Zazkis (2011) y Nilsson (2007), quienes indican que los espacios muestrales supuestos por los estudiantes no siempre coinciden con los normativos. Ello supone que los estudiantes no relacionan adecuadamente el espacio muestral con la mayor o menor posibilidad de cada resultado del experimento, una de las condiciones expuestas por Horvath y Lehrer (1998) para la comprensión del espacio muestral.
Por otro lado, en el trabajo se ha analizado la relación entre el nivel de razonamiento proporcional alcanzado por el estudiantado, en la clasificación de Noelting (1980a; 1980b) y la competencia en construcción de espacios muestrales asociados a distintos tipos de sucesos, en contextos de urnas y ruletas. Se ha encontrado asociación estadística directa entre estas variables, pero no con el curso escolar, no probada anteriormente de forma empírica, lo que confirma la dificultad de comprensión de la idea de espacio muestral y de los sucesos imposibles y seguros que no mejora con la edad.
Una conclusión directa es el interés de reforzar el razonamiento proporcional de los y las estudiantes, teniendo en cuenta sus diversos significados y su articulación progresiva (Burgos y Godino, 2020), puesto que el estudio muestra que pocos, incluso en los cursos superiores, logran el razonamiento proporcional de mayor nivel, confirmando lo expuesto en González-Forte et al. (2022) y Van Dooren et al., (2018). No obstante, el estudiantado con mayor nivel de razonamiento proporcional obtuvo mejores resultados en la construcción de espacios muestrales; por lo que este refuerzo mejoraría igualmente la comprensión de las ideas de suceso imposible y seguro, que fueron difíciles para los estudiantes, en general, al igual que en Cañizares (1997), Green (1983) y Groth (2020). Dicha dificultad implica que no se pone en relación el número de casos con la mayor o menor posibilidad de cada resultado del experimento (Horvath y Lehrer; 1998) o bien que los estudiantes pudieran tener problemas para separar bien los casos favorables y desfavorables en los experimentos propuestos (Nilsson, 2007).
La dificultad se supera, sin embargo, en el estudiantado que razona de acuerdo a los niveles de razonamiento proporcional IIA y superiores considerados por Noelting (1908a 1980b). Dada la relación entre la capacidad de construcción del espacio muestral, el razonamiento combinatorio (Batanero y Álvarez-Arroyo, 2023; Lockwood et al., 2020) y la resolución de problemas de probabilidad (Nunes et al., 2014; Langrall y Mooney, 2005), la mejora del razonamiento proporcional repercutirá en la del razonamiento probabilístico de los estudiantes, como se confirma en los resultados del presente estudio.
Los resultados sugieren, también, la necesidad de prestar atención a la comprensión del lenguaje de probabilidad por parte de los y las estudiantes, lo que podría llevarse a cabo en la enseñanza teniendo en cuenta las ideas de Groth (2020) sobre polisemia, interrelación y multidimensionalidad de dicho lenguaje. Es necesario que los estudiantes reconozcan el carácter polisémico de las palabras seguro e imposible, diferenciando su uso en la vida cotidiana y su significado en probabilidad. También se requiere comprender la interrelación entre diferentes términos asociados al lenguaje de la probabilidad, y que vayan adquiriendo este lenguaje en forma progresiva en su formación académica. Para ello, será importante que, cuando se les pide resolver problemas de probabilidad, además de las estimaciones cuantitativas de la probabilidad, se les pida añadir algunas expresiones cualitativas de la misma, puesto que en ocasiones estas se comprenden posteriormente a la adquisición de la probabilidad numérica. Ello contribuirá a que descarten los significados poco precisos de las mismas que se utilizan fuera del aula en lenguaje coloquial (Groth, 2020).
En las tareas propuestas se pide construir un espacio muestral a partir de ciertas condiciones en dos contextos diferentes (urnas y ruletas), lo que plantea un desafío para el estudiante al no ser una tarea habitual para ellos, aunque muchos de ellos, sin embargo, la han completado satisfactoriamente. Además, en nuestro trabajo previo (Hernández-Solís et al., 2021), el contexto de ruletas fue más sencillo que el de urnas, y no hemos encontrado mucha diferencia en el presente estudio en el que se incluye a estudiantes mayores que en aquel caso. Dichas tareas podrían utilizarse en el aula, para reforzar la articulación entre combinatoria y probabilidad, basada en la construcción de espacios muestrales (Lima y Borba, 2021). Al mismo tiempo podrían contribuir a la mejora del razonamiento proporcional, dada la relación entre los dos tipos de tareas y la importancia del contexto de los problemas proporcionales en su dificultad y las estrategias con que los abordan los estudiantes (Supply et al., 2023). Para finalizar, reconocemos las posibles limitaciones debidas a la muestra y tareas utilizadas, animando a otros investigadores a profundizar el tema.
Agradecimiento: Proyecto PID2022-139748NB-100
REFERENCIAS BIBLIOGRÁFICAS
Batanero, C. y Álvarez-Arroyo, R. (2023). Teaching and learning of probability. ZDM Mathematics Education, 56, 5-17. https://doi.org/10.1007/s11858-023-01511-5
Batanero, C., Godino, J. y Navarro-Pelayo, V. (1997). Combinatorial reasoning and its assessment. En I. Gal y J B. Garfield (Eds.), The assessment challenge in statistics education (pp. 239–252). IOS Press.
Batanero, C. y Hernández-Solís, LA. (2023). Razonamiento proporcional en comparación de razones de estudiantes costarricenses y españoles. Uniciencia, 37(1), 1-20. https://doi.org/10.15359/ru.37-1.21
Ben-Chaim, D., Keret, Y. e Ilany, B. S. (2012). Ratio and proportion: Research and teaching in mathematics teachers’ education. Sense Publisher. https://doi.org/10.1007/978-94-6091-784-4_2
Boyer, T.W. y Levine, S.C. (2015). Prompting children to reason proportionally: Processing discrete units as continuous amounts. Developmental Psychology, 51(5), 615-620. https://doi.org/10.1037/a0039010
Butto, C.M., Fernández, J.D., Araujo, D.C. y Ramírez, A.B. (2019). El razonamiento proporcional en educación básica. Horizontes Pedagógicos, 21(2), 39-52. https://doi.org/10.33881/0123-8264.hop.21204
Burgos, M. y Godino, J.D. (2020). Modelo ontosemiótico de referencia de la proporcionalidad. Implicaciones para la planificación curricular en primaria y secundaria. Avances de Investigación en Educación Matemática, 18, 1-20. https://doi.org/10.35763/aiem.v0i18.255
Cañizares, M.J. (1997). Influencia del razonamiento proporcional y combinatorio y de creencias subjetivas en las intuiciones probabilísticas primarias. [Tesis Doctoral, Universidad de Granada].
Carpenter, T.P., Fennema, E. y Romberg, T.A. (Eds.). (2012). Rational numbers: An integration of research. Routledge (2º edición). https://doi.org/10.4324/9780203052624
Chernoff, E. J. (2009). Sample space partitions: An investigative lens. The Journal of Mathematical Behavior, 28(1), 19-29.
Chernoff, E.J. y Zazkis, R. (2011). From personal to conventional probabilities: from sample set to sample space. Educational Studies in Mathematics, 77, 15-33. https://doi.org/10.1007/s10649-0109288-8
English, L.D. (2005). Combinatorics and the development of children’s combinatorial reasoning. En G.A. Jones (Ed,), Exploring probability in school: Challenges for teaching and learning (pp. 121-141). Springer.
Etikan, I., Musa, S.A. y Alkassim, R.S. (2016). Comparison of convenience sampling and purposive sampling. American Journal of Theoretical and Applied Statistics, 5(1), 1-4. https://doi.org/10.6224/jn.61.3.10T
González-Forte, J. M., Fernández, C., Van Hoof, J. y Van Dooren, W. (2022). Profiles in understanding operations with rational numbers. Mathematical Thinking and Learning, 24(3), 230-247. https://doi.org/10.1080/10986065.2021.1882287
Green, D. R. (1983). School pupils’ probability concepts. Teaching Statistics, 5(2), 34-42.
Groth, R.E., Bergner, J.A. y Austin, J.W. (2020). Dimensions of learning probability vocabulary. Journal for Research in Mathematics Education, 51(1), 75-104. https://doi.org/10.5951/jresematheduc.2019.0008
He, W., Yang, Y. y Gao, D. (2018). Proportional reasoning in 5- to 6-year-olds. Journal of Cognition and Development, 19(4), 389-412. https://doi.org/10.1080/15248372.2018.1495218
Hernández-Salmerón, E., López-Martín, M.M. y Batanero, C. (2017). Estudio exploratorio sobre el lenguaje del azar en educación secundaria obligatoria. En J.M. Muñoz, A. Arnal-Bailera, P. Beltrán-Pellicer, M.L. Callejo y J. Carrillo (Eds.), Investigación en Educación Matemática XXI (pp. 305-314). Universidad de Zaragoza.
Hernández-Solís, L.A., Batanero, C., Gea, M.M. y Álvarez-Arroyo, R. (2021). Construcción de espacios muestrales asociados a distintos tipos de sucesos: un estudio exploratorio con estudiantes de educación primaria. Educación Matemática, 33(1), 181-207. https://doi.org/10.24844/em3301.07
Horvath, J.K. y Lehrer, R. (1998). A model-based perspective on the development of children’s understanding of chance and uncertainty. En S. Lajoie (Ed.), Reflections on statistics: learning, teaching, and assessment in grades K-12 (pp. 121-148). Routledge.
Jones, G., Langrall, C., Thornton, C. y Mogill, A. (1997). A framework for assessing and nurturing young children’s thinking in probability. Educational Studies in Mathematics, 32, 101-125. https://doi.org/10.1023/A:1002981520728
Karplus, R., Pulos, S. y Stage, E.K. (1983). Early adolescents’ proportional reasoning on ‘rate’ problems. Educational Studies in Mathematics, 14(3), 219-233. https://doi.org/10.1007/BF00410539
Kieren, T.E. (2020). Rational and fractional numbers as mathematical and personal knowledge: Implications for curriculum and instruction. En G. Leinhardt, R. Putnam y R. Hattrup (Eds.), Analysis of arithmetic for mathematics teaching (pp. 323-371). Routledge. https://doi.org/10.4324/9781315044606
Konold, C. (1989). Informal conceptions of probability. Cognition and Instruction, 6(1), 59-98. https://doi.org/10.1207/s1532690xci0601_3
Lamon, S. J. (2007). Rational numbers and proportional reasoning: Toward a theoretical framework for research. En F. Lester (Ed.), Second handbook of research on mathematics teaching and learning (V. 1, pp. 629-667). Information Age.
Lecoutre, M.P. (1992). Cognitive models and problem spaces in “purely random” situations. Educational Studies in Mathematics, 23, 557-568. https://doi.org/10.1007/BF00540060
Langrall, C. y Mooney, E. (2005). Characteristics of elementary school students’ probabilistic reasoning. En G. Jones (Ed.), Exploring probability in school (pp. 95-119). Springer.
Lima, E. y Borba, R. (2021). Articulando combinatória e probabilidade: jovens e adultos revisitando problemas combinatórios via construção de espaços amostrais. Paradigma, 42(Extra 1), 257-284. https://doi.org/10.37618/PARADIGMA.1011-2251.2021.p257-284.id1025
Lockwood, E., Wasserman, N.H. y Tillema, E.S. (2020). A case for combinatorics: A research commentary. The Journal of Mathematical Behavior, 59, 100783. https://doi.org/10.1016/j.jmathb.2020.100783
Ministerio de Educación Pública (MEP) (2012). Programas de Estudio de Matemáticas. I, II Y III Ciclos de la Educación General Básica y Ciclo Diversificado. MEP.
Noelting, G. (1980a). The development of proportional reasoning and the ratio concept. Part I. Diferentiation of stages. Educational Studies in Mathematics, 11(2), 217-253.
Noelting, G. (1980b). The development of proportional reasoning and the ratio concept. Part II. Problem structure at succesive stages: Problem solving strategies and the mechanism of adaptive restructuring. Educational Studies in Mathematics, 11(3), 331-363.
Nunes, T., Bryant, P., Evans, D., Gottardis, L. y Terlektsi, M.-E. (2014). The cognitive demands of understanding the sample space. ZDM Mathematics Education, 46(3), 437-448. https://doi.org/10.1007/s11858-014-0581-3
Nilsson, P. (2007). Different ways in which students handle chance encounters in the explorative setting of a dice game. Educational Studies in Mathematics, 66(3), 293-315. https://doi.org/10.1007/s10649-006-9062-0
Piaget, J. e Inhelder, B. (1951). La genèse de l’idée de hasard chez l’enfant. Presses Universitaires de France.
Speiser, R. y Walter, C. (1998). Two dice, two sample spaces. Proceedings of the Fifth International Conference on Teaching Statistics (Vol. 1, pp. 61-66). International Statistical Institute.
Supply, A.S., Vanluydt, E., Van Dooren, W. y Onghena, P. (2023). Out of proportion or out of context? Comparing 8-to 9-year-olds’ proportional reasoning abilities across fair-sharing, mixtures, and probability contexts. Educational Studies in Mathematics, 113, 1-18. https://doi.org/10.1007/s10649-023-10212-5
Van Dooren, W., Vamvakoussi, X. y Verschaffel, L. (2018). Proportional reasoning. International Academy of Education.
Zapata-Cardona, L. (2018). Supporting young children to develop combinatorial reasoning. En A. Leavy, M. Meletiou-Mavrotheris y E. Paparistodemou (Eds.), Statistics in early childhood and primary education (pp. 257-272). Springer: https://doi.org/10.1007/978-981-13-1044-7_15
Como citar:
Hernández-Solís, L.A., Batanero, C. y Gea, M.M. (2024). Relación entre la construcción de espacios muestrales y el razonamiento proporcional de estudiantes costarricenses. Revista de Educación Estadística, 3, 1-28. https://doi.org/10.29035/redes.3.1.1
ANEXO. CUESTIONARIOS
CUESTIONARIO A
Ítem 1
Elena y Juan preparan limonada. Elena mezcla 2 vasos de zumo de limón con 3 vasos de agua. Juan mezcla 1 vaso de zumo de limón con 3 vasos de agua. Todos los vasos contienen la misma cantidad de líquido. Observa el dibujo.
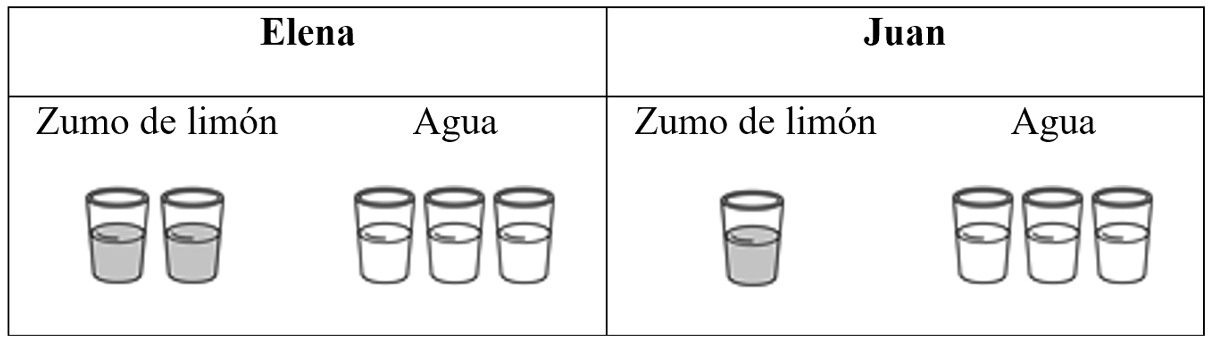
¿Cuál de las dos limonadas sabe más a limón?
( ) La de Elena.
( ) La de Juan.
( ) Las dos igual.
( ) No lo sé.
Explica por qué das esta respuesta:
Ítem 3
Elena mezcla 2 vasos de zumo de limón con 2 vasos de agua. Juan mezcla 4 vasos de zumo de limón con 4 vasos de agua. Todos los vasos contienen la misma cantidad de líquido. Observa el dibujo.
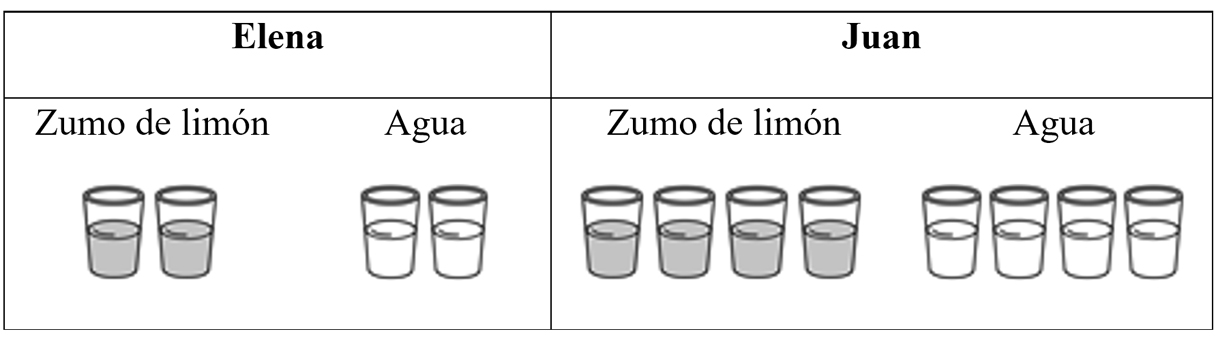
¿Cuál de las dos limonadas sabe más a limón?
( ) La de Elena.
( ) La de Juan.
( ) Las dos igual.
( ) No lo sé.
Explica por qué das esta respuesta:
Ítem 5
Elena mezcla 3 vasos de zumo de limón con 1 vaso de agua. Juan mezcla 4 vasos de zumo de limón con 2 vasos de agua. Todos los vasos contienen la misma cantidad de líquido. Observa el dibujo.
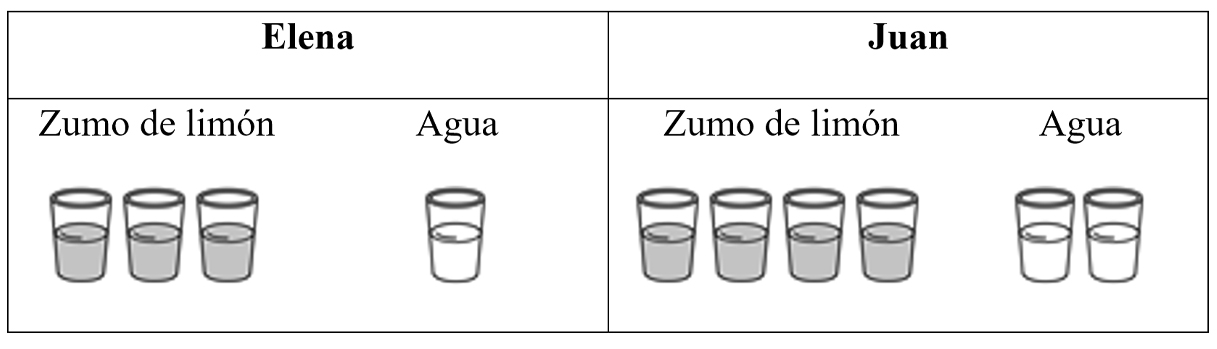
¿Cuál de las dos limonadas sabe más a limón?
( ) La de Elena.
( ) La de Juan.
( ) Las dos igual.
( ) No lo sé.
Explica por qué das esta respuesta:
Ítem 7
María y Esteban juegan con una ruleta dividida en seis partes iguales. María gana un premio si la aguja que gira cae en una parte pintada de color negro y Esteban gana si cae en una parte pintada de color blanco. Pinta en las siguientes ruletas tantas partes negras y blancas, como consideres oportuno, para que ocurra:
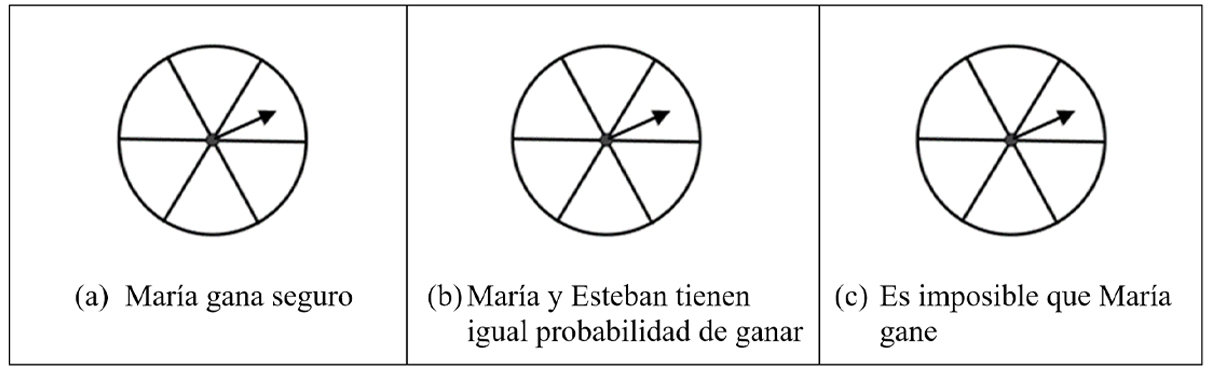
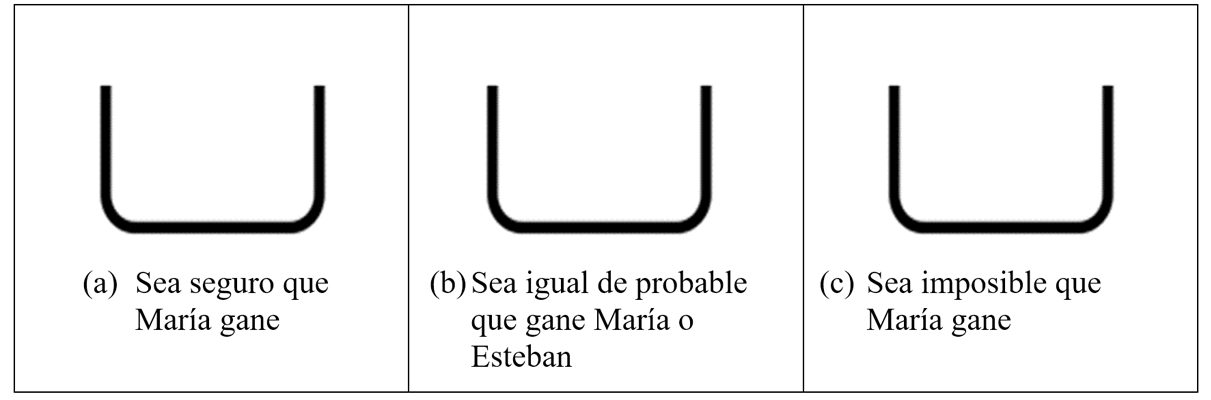
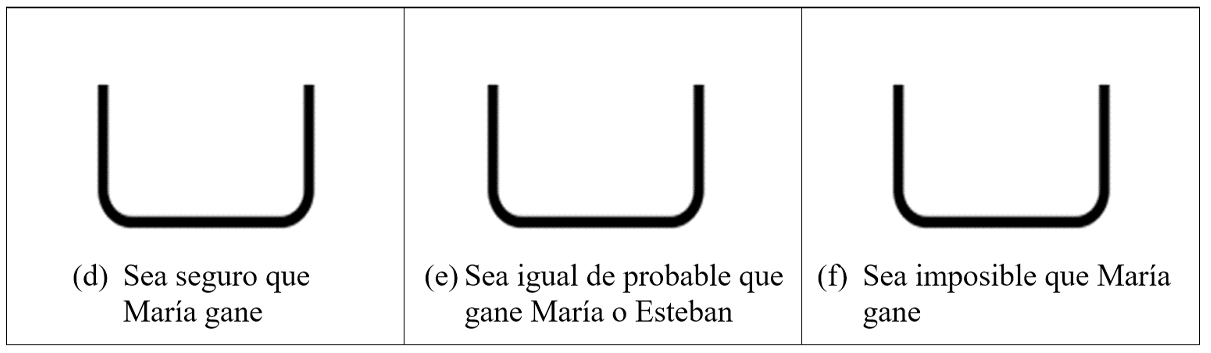
Ítem 8
En un juego se saca, sin mirar, una bola de una caja. Si ésta es de color negro María gana y si es de color blanco Esteban gana. Dibuja y colorea en las siguientes cajas tantas bolas negras y blancas, como consideres oportuno, para que:
CUESTIONARIO B
Ítem 2
Elena y Juan preparan limonada. Elena mezcla 5 vasos de zumo de limón con 1 vaso de agua. Juan mezcla 5 vasos de zumo de limón con 4 vasos de agua. Todos los vasos contienen la misma cantidad de líquido. Observa el dibujo.
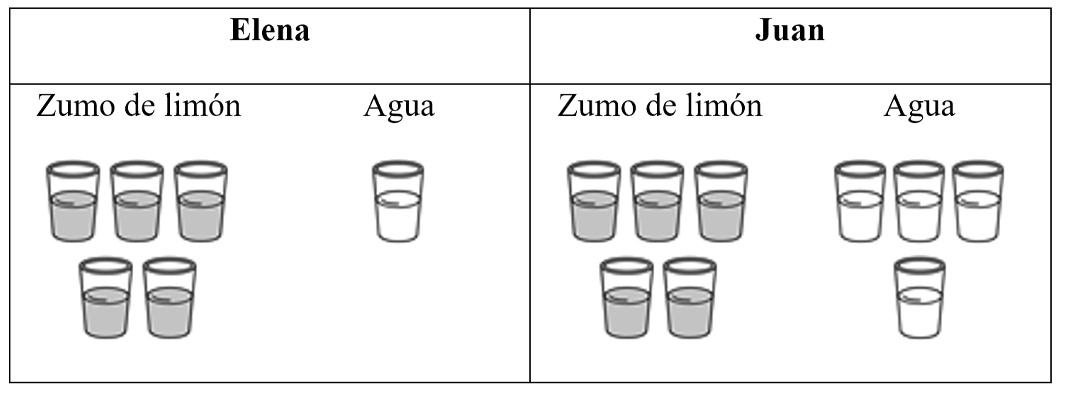
¿Cuál de las dos limonadas sabe más a limón?
( ) La de Elena.
( ) La de Juan.
( ) Las dos igual.
( ) No lo sé.
Explica por qué das esta respuesta:
Ítem 4
Elena mezcla 3 vasos de zumo de limón con 1 vaso de agua. Juan mezcla 6 vasos de zumo de limón con 2 vasos de agua. Todos los vasos contienen la misma cantidad de líquido. Observa el dibujo.
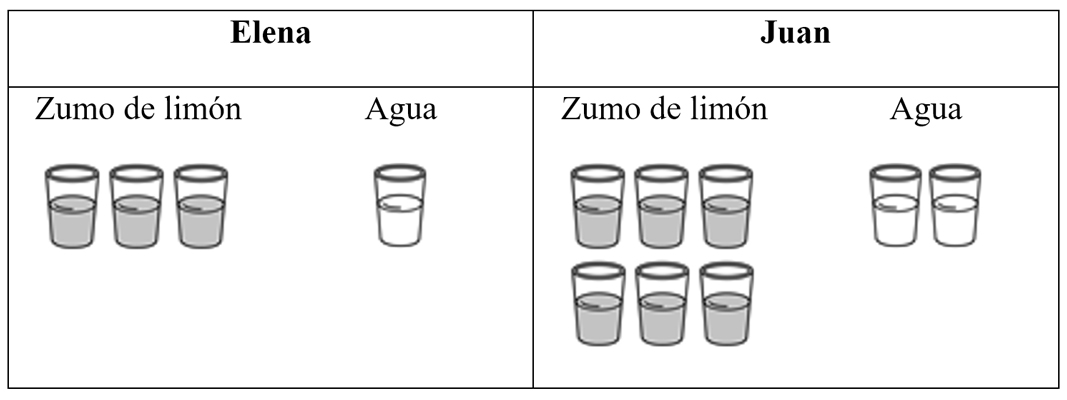
¿Cuál de las dos limonadas sabe más a limón?
( ) La de Elena.
( ) La de Juan.
( ) Las dos igual.
( ) No lo sé.
Explica por qué das esta respuesta:
Ítem 6
Elena mezcla 3 vasos de zumo de limón con 2 vasos de agua. Juan mezcla 4 vasos de zumo de limón con 3 vasos de agua. Todos los vasos contienen la misma cantidad de líquido. Observa el dibujo.
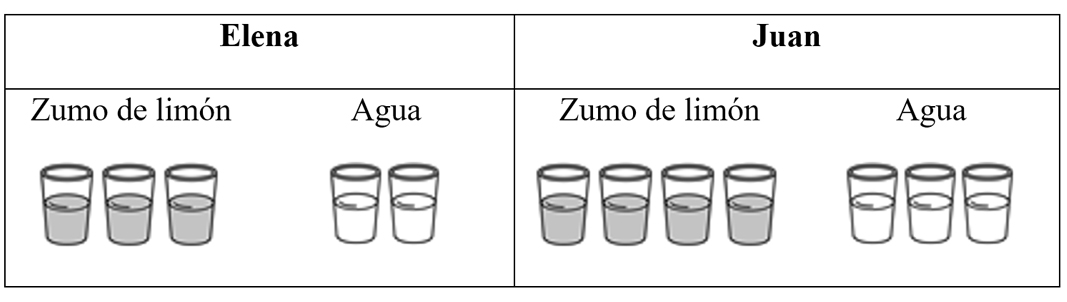
¿Cuál de las dos limonadas sabe más a limón?
( ) La de Elena.
( ) La de Juan.
( ) Las dos igual.
( ) No lo sé.
Explica por qué das esta respuesta:
Ítem 7
María y Esteban juegan con una ruleta dividida en seis partes iguales. María gana un premio si la aguja que gira cae en una parte pintada de color negro y Esteban gana si cae en una parte pintada de color blanco. Pinta en las siguientes ruletas tantas partes negras y blancas, como consideres oportuno, para que ocurra:
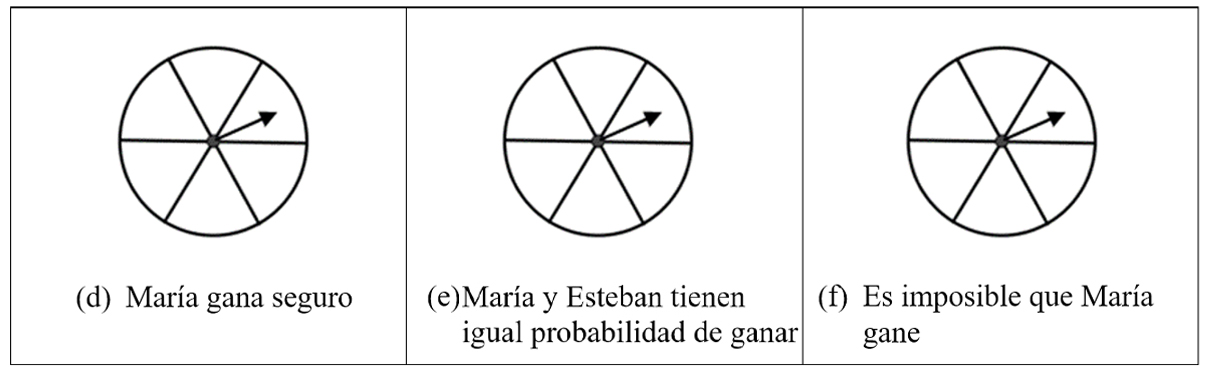
Ítem 8
En un juego se saca, sin mirar, una bola de una caja. Si ésta es de color negro María gana y si es de color blanco Esteban gana. Dibuja y colorea en las siguientes cajas tantas bolas negras y blancas, como consideres oportuno, para que:

Esta obra está bajo una licencia de Creative Commons
Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional.
1*Autor de correspondencia: batanero@ugr.es (C. Batanero)
https://orcid.org/0000-0003-2956-8102 (lhernandez@uned.ac.cr).
