Revista de Educación Estadística https://revistaeduest.ucm.cl/ Vol. 2, n. 1, 1-21, abr. 2023 - sep. 2023 ISSN 2810-6164

 

DOI: https://doi.org/10.29035/redes.2.1.6

 

EL RAZONAMIENTO PROPORCIONAL Y PROBABILÍSTICO EN LA ENSEÑANZA CHILENA: UN ANÁLISIS DE LAS NORMATIVAS CURRICULARES

O raciocínio proporcional e probabilístico no ensino chileno: Uma análise das normativas curriculares

Proportional and probabilistic reasoning in Chilean education: An analysis of curriculum regulations

 

Carmen Gloria Aguayo-Arriagada*1

Universidad de Almería (Almería, España)

Diego Ortiz Flores2

Universidad de Almería (Almería, España)

María del Mar López-Martín3

Universidad de Almería (Almería, España)

 

Resumen

En Chile, el Ministerio de Educación (MINEDUC) es responsable de establecer los lineamientos curriculares en diferentes niveles educativos, identificando los elementos clave que influyen en los procesos de enseñanza y aprendizaje de los temas. Este artículo examina las normativas educativas vigentes en Chile, con un enfoque en las materias de matemáticas desde séptimo de Educación Básica a segundo de Educación Media. Se ha realizado un estudio cualitativo y descriptivo de análisis de contenido, con el objetivo de analizar de manera individual la presencia del razonamiento proporcional y probabilístico en el contexto. Este estudio nos permite comprender la presencia de estos conceptos y cómo se relacionan entre sí. Los resultados muestran que el contenido de proporcionalidad se introduce tarde en el proceso educativo, mientras que el de probabilidad está presente en la mayoría de los niveles educativos. Además, se observa que los objetivos de proporcionalidad no están contextualizados en términos de probabilidad, a diferencia de los objetivos de probabilidad, que se relacionan en gran medida con el razonamiento proporcional.

Palabras clave: Proporcionalidad, Probabilidad, Currículo chileno, Razonamiento probabilístico, Educación Media.

 

Resumo

No Chile, o Ministério da Educação (MINEDUC) é responsável por estabelecer as diretrizes curriculares em diferentes níveis educacionais, identificando os elementos-chave que influenciam nos processos de ensino e aprendizagem das disciplinas. Este artigo examina as normas educativas vigentes no Chile, com foco nas matérias de matemática do sétimo ano do Ensino Fundamental ao segundo ano do Ensino Médio. Foi realizado um estudo qualitativo e descritivo de análise de conteúdo, com o objetivo de analisar individualmente a presença do raciocínio proporcional e probabilístico nesse contexto. Este estudo permite compreender a presença desses conceitos e como eles se relacionam entre si. Os resultados mostram que o conteúdo de proporcionalidade é introduzido tarde no processo educativo, enquanto a probabilidade está presente na maioria dos níveis educacionais. Além disso, observa-se que os objetivos de proporcionalidade não estão contextualizados em termos de probabilidade, ao contrário dos objetivos de probabilidade, que estão amplamente relacionados ao raciocínio proporcional.

Palavras-chave: Proporcionalidade, Probabilidade, Currículo chileno, Raciocínio probabilístico, Ensino secundário.

 

Abstract

In Chile, the Ministry of Education (MINEDUC) is responsible for establishing curriculum guidelines at different educational levels, identifying key elements that influence teaching and learning processes of subjects. This article examines the current educational regulations in Chile, with a focus on mathematics subjects from seventh grade of Basic Education to second grade of Media Education. A qualitative and descriptive content analysis study has been carried out with the aim of individually analyzing the presence of proportional and probabilistic reasoning in this context. This study allows us to understand the presence of these concepts and how they relate to each other. The results show that the content of proportionality is introduced late in the educational process, while probability is present in most educational levels. In addition, it is observed that the objectives of proportionality are not contextualized in terms of probability, unlike the objectives of probability, which are largely related to proportional reasoning.

Keywords: Proportionality, Probability, Chilean curriculum, Probabilistic reasoning, Secondary Education.

 

Recibido: 03/04/2023 - Aceptado: 23/06/2023

 

1. INTRODUCCIÓN

 

Hoy en día, la enseñanza de las matemáticas se enfoca en el desarrollo del razonamiento matemático, tanto deductivo como inductivo, destacando el hecho de formar a ciudadanos que posean una alfabetización matemática, entendida, en el marco de la Organización para la Cooperación y el Desarrollo Económicos (OECD), como:

La alfabetización matemática es la capacidad de un individuo de razonar matemáticamente y de formular, emplear e interpretar las matemáticas para resolver problemas en una amplia variedad de contextos de la vida real. Esto incluye conceptos, procedimientos, datos y herramientas para describir, explicar y predecir fenómenos. Ayuda a los individuos a conocer el papel que cumplen las matemáticas en el mundo y hacer los juicios y tomar las decisiones bien fundamentadas que necesitan los ciudadanos reflexivos, constructivos y comprometidos del siglo XXI. (OECD, 2021, p. 7)

Para fomentar el desarrollo de habilidades para la resolución de problemas, los contenidos matemáticos se categorizan en: cambios y relaciones, espacio y forma, cantidad, e incertidumbre y datos (OECD, 2013). En esta última categoría, el razonamiento probabilístico adquiere una gran importancia, ya que permite comprender y analizar situaciones que implican incertidumbre y variabilidad, y tomar decisiones basadas en la probabilidad de ocurrencia de eventos. En un mundo cada vez más complejo e incierto, el desarrollo de habilidades de razonamiento probabilístico se vuelve cada vez más relevante, en diversos ámbitos, como la economía, la medicina y la política, así como para comprender situaciones cotidianas como el pronóstico del clima, los resultados deportivos o el diagnóstico médico, entre otras (Vásquez y Alsina, 2019; Velasco et al., 2022).

En el ámbito educativo, se reconoce ampliamente la importancia del razonamiento probabilístico como una habilidad esencial para la toma de decisiones fundamentadas en situaciones de incertidumbre (Batanero, 2006). De hecho, este enfoque se refleja en las directrices curriculares de muchos países (García-García et al., 2022; Merino y Reyes, 2013; Vásquez y Alsina, 2015; Vásquez y Cabrera, 2022). En este contexto, la adquisición de habilidades de razonamiento proporcional, que implica la habilidad de establecer relaciones multiplicativas entre dos cantidades y extenderlas a otro par de cantidades (Lamon, 2007), ha sido identificada como un componente fundamental para garantizar una instrucción exitosa en probabilidad (Bryant y Nunes, 2012; Burgos et al., 2022). Aunque existe una discusión conceptual sobre la relación entre el razonamiento proporcional y el probabilístico, desarrollar habilidades de pensamiento proporcional resulta esencial para comprender y cuantificar adecuadamente la probabilidad, ya que se trata de una medida basada en proporciones (Bryant y Nunes, 2012; Falk et al., 2012), y su comprensión sólida resulta fundamental para resolver situaciones probabilísticas en contextos reales. Por lo que, es importante impulsar una educación que fomente el aprendizaje activo y reflexivo, que permita a los estudiantes desarrollar habilidades en ambos tipos de razonamiento, proporcional y probabilístico, ya que esto les permitiría tomar decisiones informadas en situaciones reales y complejas.

A pesar de la importancia de los razonamientos proporcional y probabilístico en la vida cotidiana, son escasas las investigaciones que han analizado su integración en las normativas curriculares. No obstante, algunos autores han realizado análisis interesantes en este ámbito, incluyendo contenidos estadísticos y probabilísticos, contribuyendo a la comprensión de cómo se abordan en los sistemas educativos. Por ejemplo, Batanero et al. (2012, 2014) sugieren que la enseñanza de la estadística debe ser más exploratoria y reforzar aspectos intuitivos, en todos los niveles de educación obligatoria. En el contexto chileno, Pino et al. (2014) realizaron un análisis de los gráficos estadísticos en las bases curriculares chilenas de Matemáticas y Ciencias en Educación Primaria. Sus resultados revelaron una amplia variedad de actividades que permiten un enfoque interdisciplinario en diferentes contextos. En la etapa de Educación Media, Sánchez y Ruiz (2020) analizaron propuestas metodológicas para la enseñanza de la estadística en programas de séptimo y octavo grado en Chile. Las actividades analizadas se centran en el concepto de muestras, con cierta integración de medidas de tendencia central y posición. Sin embargo, el programa de octavo grado carecía de estos componentes, lo que restringe el desarrollo del razonamiento inferencial. Sin embargo, ambos estudios ofrecen valiosas sugerencias para que los profesores mejoren sus prácticas de enseñanza.

Basándonos en las consideraciones previas, el propósito fundamental de este estudio es examinar la presencia y el grado de evolución del razonamiento proporcional y probabilístico en las normativas curriculares de Educación Media y Básica en Chile. El presente trabajo se distribuye en cuatro secciones: en la Sección 2 se presenta la organización del sistema educativo chileno y los diferentes documentos curriculares que el Ministerio de Educación en Chile, MINEDUC, facilita a los centros educativos; en la Sección 3, se analiza el razonamiento proporcional y probabilístico en los documentos curriculares de séptimo de Enseñanza Básica a segundo de Enseñanza Media; para finalizar, en la Sección 4 se presentan las reflexiones finales.

 

2. SISTEMA EDUCATIVO CHILENO

 

En el ámbito de la investigación educativa, el currículo es considerado como un conjunto de objetivos, contenidos, criterios de aprendizaje, metodologías e indicadores evaluativos que los estudiantes deben alcanzar al finalizar un determinado ciclo educativo (Dolores, 2012), cuya finalidad es presentar y organizar la enseñanza, según las características propias de cada comunidad y basado en el contexto donde se desarrolla el proceso de aprendizaje (Rodríguez, 2013).

El término currículo fue introducido en Chile durante el último tercio del siglo XIX, cuando se implementó un plan de estudios de tipo concéntrico basado en el modelo alemán (Cox, 2011). Ruz-Fuenzalida (2020) identifica tres momentos importantes de la historia curricular de Chile en los últimos 30 años. Tras la dictadura cívico-militar, en la década de los noventa, se implementaron ajustes curriculares en la Ley Orgánica Constitucional de Enseñanza (LOCE). En 2009 se realizó un importante ajuste curricular para fortalecer y dar coherencia al currículo en todos los niveles educativos, integrando habilidades y actitudes. Tres años después, se crearon nuevas bases curriculares para los primeros seis cursos de Educación Básica. Recientemente, y debido a la situación de pandemia por la COVID-19, la Unidad de Currículum y Evaluación del Ministerio de Educación implementó una priorización del currículum para el sistema escolar.

En la actualidad, el sistema educativo obligatorio en Chile se organiza en tres niveles formativos: Educación Parvularia o Pre-Básica (4-5 años), Educación Básica (6-12 años) desde primer año hasta sexto año, y Educación Media (13-18 años) que comienza en séptimo básico y culmina en cuarto medio. Esta última etapa educativa se estructura en: (1) científicos, humanistas y artísticos, que están enfocados en preparar a sus estudiantes para la Prueba de Acceso a la Educación Superior (PAES); y (2) educación técnica profesional, que prepara a los estudiantes para que, al terminar su ciclo de enseñanza media, obtengan un título de conocimiento técnico en algún área laboral.

Los centros educativos chilenos se rigen por el currículo oficial, supervisado por el MINEDUC, que se apoya en las bases curriculares como elemento clave del proceso de enseñanza-aprendizaje, que incluyen los objetivos generales de Educación Básica y Educación Media, así como los objetivos transversales para cada área de conocimiento. Dicho documento establece la organización curricular, teniendo en cuenta las habilidades, los ejes temáticos y las actitudes a trabajar en cada una de las áreas. De igual forma, para cada nivel académico se establecen los objetivos de aprendizaje (OA) por habilidades y ejes temáticos. Atendiendo a los OA definidos en las bases curriculares, se establece una categorización de estos, definiendo los aprendizajes basales, considerados como OA fundamentales para el desarrollo de trayectorias formativas en cada asignatura, nivel y ciclo; los Aprendizajes Complementarios, que complementan y enriquecen los aprendizajes basales, pudiendo integrarse y articularse dentro y entre asignaturas, y los Aprendizaje Transversales, destacando los objetivos relacionados con la convivencia, el bienestar y la salud mental, así como la formación ética de los estudiantes.

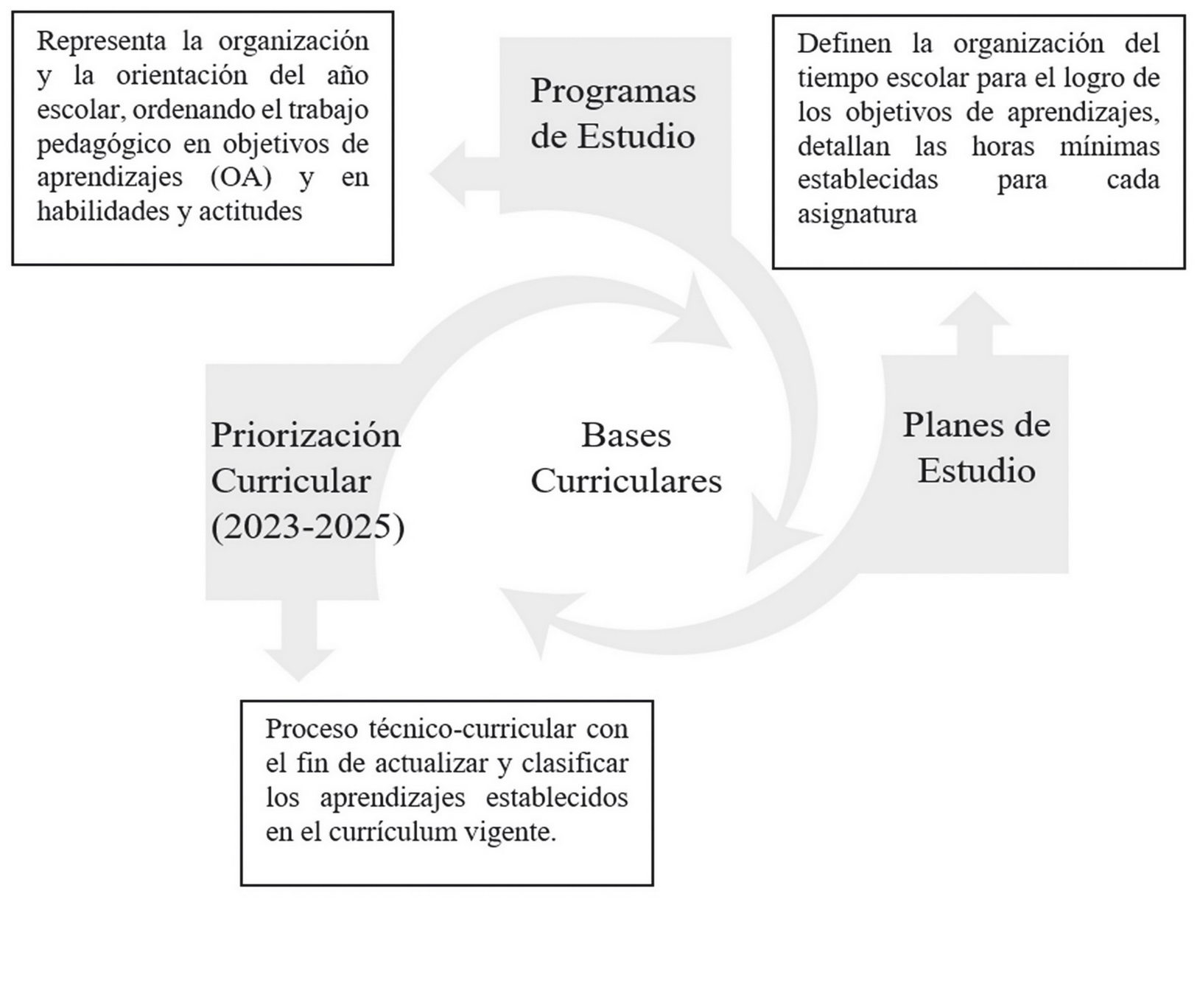
La estructura de las bases curriculares posee una importancia vital, debido a su impacto significativo en la enseñanza y el aprendizaje de las materias en el sistema educativo chileno. Además de las bases curriculares, el Ministerio de Educación proporciona otros documentos curriculares de apoyo, como los programas de estudio, planes de estudio y la priorización curricular 2023-2025 (véase Figura 1). Los programas de estudio incluyen los objetivos de aprendizaje y sus respectivos indicadores de evaluación, los cuales representan las diferentes formas en las que un estudiante puede demostrar su aprendizaje. Además, estos programas ofrecen estrategias didácticas y pedagógicas, así como una lista de conocimientos, habilidades y actitudes esperadas para los estudiantes. Los profesores tienen la libertad de ajustar estas propuestas a las necesidades de su clase y centrarse en los objetivos que consideren más importantes para sus estudiantes. Por otro lado, los planes de estudio definen la distribución del tiempo y la estructura escolar de cada asignatura que se imparte en el centro educativo.

 

Figura 1

Documentos curriculares oficiales en Chile

La suspensión prolongada de las clases presenciales, por la pandemia de la COVID-19 y dos años de clases tanto online como híbridas, trajo consigo diversos problemas en los diferentes centros educativos, principalmente en la disminución considerable en el aprendizaje de los estudiantes, la salud mental de los diferentes actores del proceso educativo, evidenciando las cifras elevadas de bajas docentes, ausentismo escolar por problemas de conectividad y problemas en la convivencia escolar en la vuelta a la “normalidad” (MINEDUC, 2023). En este contexto, el MINEDUC pone a disposición un plan de reactivación educativa, como agenda educativa 2023-2025, con las diferentes priorizaciones curriculares, que tienen como objetivo dar respuesta integradora a las necesidades educativas emergidas durante la pandemia.

Sin embargo, es importante tener en cuenta que, a diferencia de las bases curriculares, según la Ley General de Educación, los establecimientos educacionales tienen la libertad de elegir entre aplicar los planes y programas de estudio establecidos por el Ministerio o desarrollar sus propios programas para las asignaturas obligatorias. No obstante, resulta fundamental considerar estos documentos en la planificación y ejecución de la educación, debido a su trascendencia y su impacto en la enseñanza y el aprendizaje de las materias en el sistema educativo chileno.

 

3. LA PROPORCIONALIDAD Y PROBABILIDAD EN LOS DOCUMENTOS CURRICULARES CHILENOS

 

3.1. Metodología

 

En el marco de esta investigación, se emplea una metodología cualitativa basada en el análisis de contenido, siguiendo las directrices propuestas por Salgado (2007), ya que se pretende tener una visión de la presencia de los contenidos de proporcionalidad y probabilidad en los documentos curriculares actuales de Educación Media, así como identificar posibles relaciones entre estos dos temas.

Para tal fin, se analizarán las últimas normativas y lineamientos establecidos por el Ministerio de Educación, en los que se abordan los contenidos de proporcionalidad y probabilidad. Por tanto, destacamos que los planes de estudio no se analizarán, ya que estos solamente recogen la distribución horaria y estructura escolar de las materias en cada curso, sin contemplar los contenidos matemáticos específicos de cada etapa. Para la recogida de información se ha seguido el siguiente plan de actuación (Cohen et al., 2007):

1. Selección de los documentos curriculares actuales, donde se identifican contenidos y objetivos asociados a la proporcionalidad y la probabilidad.

2. Identificación de unidades de análisis: Se han seleccionado los Objetivos de Aprendizaje (OA) establecidos en las bases curriculares correspondientes a Educación Media y en sus respectivas priorizaciones, y las unidades de aprendizaje que se recogen en los programas de estudio.

3. En cada una de las secciones analizadas, se ha identificado la presencia de la proporcionalidad y la probabilidad en los OA de las bases curriculares y sus respectivas priorizaciones. También se ha realizado una codificación y su posterior estudio descriptivo, de las propuestas de actividades en cada una de las unidades de aprendizaje recogidas en los programas de estudio, teniendo en cuenta los OA y las habilidades que se ponen en juego.

 

3.2. Proporcionalidad y probabilidad en las bases curriculares chilenas

 

A lo largo de la etapa previa a la Educación Media, se ha observado que el contenido de probabilidad se encuentra presente de manera constante en el currículo educativo chileno. Según las directrices establecidas por el Ministerio de Educación (MINEDUC, 2018), este contenido se aborda desde segundo año básico y se mantiene a lo largo de todo el ciclo educativo, hasta la culminación de esta etapa. El propósito principal, es el desarrollo de habilidades y competencias relacionadas con el razonamiento probabilístico y asentar las bases para comprender y utilizar conceptos y herramientas probabilísticas, de manera efectiva, en etapas superiores. En particular, se promueve la comprensión de la aleatoriedad a través de juegos cotidianos y se presenta una secuencia gradual en la enseñanza de la probabilidad, desde conceptos básicos hasta la aplicación de reglas probabilísticas para resolver problemas. Esta continuidad en la inclusión de la probabilidad en el currículo, demuestra la importancia que se le atribuye en el proceso educativo.

Sin embargo, el estudio de la proporcionalidad en dicha etapa es limitado, ya que se aborda con un solo objetivo de aprendizaje en sexto, no articulándose con otros objetivos previos, y solo se espera que los estudiantes tengan conocimientos básicos en fracciones y sus operaciones. Concretamente, al término de este ciclo, los estudiantes serán capaces de (1) hacer representaciones concretas y pictóricas de una razón, (2) representar de diversas formas la razón, por ejemplo, 3∶5, 3/5 o 3 es a 5, (3) identificar en contextos reales la razón a través de la resolución de problemas.

En Educación Media, la probabilidad es enseñada de manera continua desde séptimo hasta segundo medio, con una progresión curricular gradual que va desde una estimación de probabilidad y contextualización de situaciones, hasta una que requieren un nivel de cálculo y aplicación de conceptos matemáticos y estadísticos más avanzados (véase Tabla 1).

Durante el proceso de aprendizaje, se espera que los estudiantes sean capaces de abordar situaciones probabilísticas, empleando herramientas propias del razonamiento proporcional, tales como razones, fracciones y porcentajes. Un claro ejemplo de esto se encuentra en el séptimo grado, específicamente en el OA18, donde se emplean fracciones para calcular las frecuencias relativas de los resultados de un experimento aleatorio. Además, en el OA19 se establece una relación entre estas frecuencias relativas observadas y la probabilidad teórica esperada. Esta conexión entre fracciones, frecuencias relativas y probabilidad teórica, permite observar la presencia del razonamiento proporcional en situaciones probabilísticas. Al analizar los contenidos abordados en cursos posteriores, se observa que los conceptos introducidos en el séptimo grado continúan siendo relevantes. Específicamente, se destacan los contenidos relacionados con la combinatoria, los cuales son necesarios para el cálculo de probabilidades desde un enfoque teórico. Estos conceptos amplían y fortalecen la comprensión de los estudiantes sobre el razonamiento proporcional y su aplicación en contextos probabilísticos.

 

Tabla 1

Objetivos de aprendizajes de probabilidad de 7º a 2º de Educación Media (MINEDUC, 2015)

Curso	Objetivos de Aprendizaje
7º E.B.	MA07 OA18: Explicar las probabilidades de eventos obtenidos por medio de experimentos de manera manual y/o con software educativo: Estimándolas de manera intuitiva, utilizando frecuencias relativas, relacionándolas con razones, fracciones o porcentaje. (p. 109) MA07 OA19: Comparar las frecuencias relativas de un evento obtenidas al repetir un experimento de forma manual y/o con software educativo, con la probabilidad obtenida de manera teórica, usando diagramas de árbol, tablas o gráficos. (p. 109)
8º E.B.	MA08 OA17: Explicar el principio combinatorio multiplicativo: A partir de situaciones concretas, representándolo con tablas y árboles regulares, de manera manual y/o con software educativo, utilizándolo para calcular la probabilidad de un evento compuesto. (p. 115)
1º E.M.	MA1M OA14: Desarrollar las reglas de las probabilidades, la regla aditiva, la regla multiplicativa y la combinación de ambas, de manera concreta, pictórica y simbólica, de manera manual y/o con software educativo, en el contexto de la resolución de problemas. (p. 120)
2º E.M.	MA2M OA10: Mostrar que comprenden las variables aleatorias finitas: Definiendo la variable, determinando los posibles valores de la incógnita, calculando su probabilidad, graficando sus distribuciones. (p. 124)
	MA2M OA11: Utilizar permutaciones y la combinatoria sencilla para calcular probabilidades de eventos y resolver problemas. (p. 125)
	MA2M OA12: Mostrar que comprenden el rol de la probabilidad en la sociedad: Revisando informaciones de los medios de comunicación, identificando suposiciones basadas en probabilidades, explicando cómo una probabilidad puede sustentar suposiciones opuestas, explicando decisiones basadas en situaciones subjetivas o en probabilidades. (p. 125)

 

Respecto a la proporcionalidad en las bases curriculares, se observa una presencia escueta con solo dos objetivos de aprendizaje incorporados en el eje de aprendizaje Álgebra y Funciones para séptimo básico, y en el eje de Geometría para primero medio (véase Tabla 2). En séptimo se aborda el reconocimiento de proporcionalidades directas e inversas, la elaboración de tablas de valores y gráficos, y la resolución de problemas, mientras que, en primero medio, se centra en aplicar el concepto de proporcionalidad y las propiedades de semejanza en situaciones cotidianas. En dicho curso, el objetivo OA08 de proporcionalidad se considera conocimiento base para otros objetivos, ya que en él se promueve la adquisición del concepto de proporción y razón, requisito esencial para los objetivos OA18 y OA19, donde se espera que los estudiantes resuelvan situaciones probabilísticas a través de la comparación de frecuencias relativas o aplicando “la regla de Laplace”. Por otro lado, en primero medio, el OA10 de proporcionalidad se centra en el uso de la proporcionalidad para resolver situaciones que involucren la semejanza, conocimiento fundamental en la comprensión de las reglas de probabilidad, conocimiento abordado en el OA14.

Los objetivos de aprendizaje para el contenido de proporcionalidad son esenciales, al igual que en el caso de la probabilidad, ya que permiten mantener una continuidad pedagógica y se relacionan con otros objetivos de aprendizaje, tales como la enseñanza de la geometría, las funciones y la probabilidad.

 

Tabla 2

Objetivos de aprendizajes de proporcionalidad de 7º a 2º de Educación Media (MINEDUC, 2015)

Curso	Objetivos de Aprendizaje
7º E.B.	MA07 OA08: Mostrar que comprenden las proporciones directas e inversas: Realizando tablas de valores para relaciones proporcionales, graficando los valores de la tabla, explicando las características de la gráfica, resolviendo problemas de la vida diaria y de otras asignaturas. (p. 108)
1º E.M.	MA1M OA10: Aplicar propiedades de semejanza y de proporcionalidad a modelos de escala y otras situaciones de la vida diaria y otras asignaturas. (p. 122)

 

Al realizar el estudio comparativo entre la Tabla 1 y la Tabla 2, se puede apreciar una brecha entre la enseñanza de la probabilidad y la proporcionalidad, ya que solamente se abordan de forma conjunta en séptimo básico y primero medio. Esta situación revela una separación entre ambos temas, a pesar de su interrelación y el potencial enriquecimiento que brinda el abordaje conjunto para una mejor comprensión de la probabilidad.

 

3.3. Proporcionalidad y probabilidad en los programas de estudio chilenos

 

Los programas de estudio están diseñados para proporcionar una clara organización de los objetivos de aprendizaje a lo largo del año escolar. Esta estructura permite a los profesores enfocar su enseñanza de manera efectiva, asegurando que los estudiantes obtengan el conocimiento y las habilidades necesarias para alcanzar los objetivos educativos requeridos. Entre estas habilidades se encuentran la resolución de problemas, la representación, el modelado, la argumentación y la comunicación.

Estos documentos curriculares están compuestos por diversas unidades de aprendizaje que se organizan en función de los OA establecidos en las bases curriculares (véase Tabla 1). Cada unidad de aprendizaje se complementa con tres actividades de evaluación que permiten evaluar el logro de algunos de los OA contemplados en ella. Dichos objetivos, se vinculan a una serie de indicadores de evaluación y actividades específicas que promueven el desarrollo de habilidades y que son sugerencias metodológicas que deben enriquecerse con el uso del libro del estudiante. De esta manera, se asegura que se adquieran, de manera efectiva, tanto los conocimientos como las habilidades necesarias para alcanzar los objetivos educativos propuestos.

En relación a la proporcionalidad y la probabilidad, la Tabla 3 resume el número de actividades según la unidad de aprendizaje (UA), los OA y las habilidades a desarrollar en función a dichos objetivos. Se evidencia que el contenido de probabilidad siempre está presente en la misma unidad de aprendizaje, mientras que la proporcionalidad se trabaja en la unidad dos en séptimo grado y en la unidad tres en primero medio. En relación a las habilidades de resolución de problemas (RP), representación (R), modelación (M) y argumentación y comunicación (AC), se evidencia una variación en la frecuencia de su abordaje, dependiendo del curso y el objetivo de aprendizaje (OA) establecido para cada nivel educativo. Estos datos reflejan cómo se priorizan y abordan diferentes habilidades a lo largo de los cursos y unidades de aprendizaje, dejando de lado el desarrollo de otras habilidades.

 

Tabla 3

Frecuencia (%) de las habilidades trabajadas según objetivos de aprendizaje en cada unidad didáctica

Curso	UA	OA	Nº Act.	Habilidades
				RP	R	M	AC
7º E.B.	2	8(*)	10	4 (40%)	3 (30%)	2 (20%)	2 (20%)
	4	18	6	-	3 (50%)	-	4 (66,7%)
	4	19	6	-	4 (66,7%)	-	4 (66,7%)
8º E.B.	4	17	6	5 (83,3%)	3 (50%)	1 (17,7%)	6 (100%)
1º E.M.	3	10(*)	9	4 (44,4%)	-	2 (22,2%)	3 (33,3%)
	4	14	8	8 (100%)	7 (87,5%)	-	5 (62,5%)
2º E.M.	4	10	7	3 (42,9%)	4 (57,1%)	-	-
	4	11	8	5 (62,5%)	-	2 (25%)	1 (12,5%)
	4	12	9	2 (22,2%)	-	6 (66,7%)	3 (33,3%)

Nota. (*) hace referencia a los objetivos de aprendizaje de proporcionalidad.

 

De forma general, se observa que las actividades propuestas para un mismo OA no cubren todas las habilidades, y estas adquieren diferentes niveles de importancia, según el curso y el objetivo correspondiente. Por ejemplo, en la unidad de aprendizaje dos del curso de séptimo, el 40% de las habilidades se enfocan en la resolución de problemas, mientras que en la unidad didáctica 4 del mismo curso, el énfasis está en la representación y argumentación y comunicación. En contraste, se observa una diferencia notable en el caso de octavo grado, donde las actividades relacionadas con el objetivo de aprendizaje OA17 abordan las cuatro habilidades de manera significativa. En este caso, se pone un fuerte énfasis en la resolución de problemas y en la argumentación y comunicación, reflejándose la de esta última habilidad en la totalidad de las actividades propuestas en torno a dicho objetivo. Esta distribución equitativa de las habilidades demuestra una intención clara de fomentar un enfoque integral en el desarrollo de los estudiantes, promoviendo tanto la capacidad de resolver problemas matemáticos como la habilidad de comunicar y argumentar sus procesos y resultados de manera efectiva.

Asimismo, se evidencia una variación en la distribución de habilidades en los cursos de primero y segundo de Educación Media, destacando en primero la presencia de habilidades de resolución de problemas en el OA14, con un 100% de frecuencia, y en segundo, la modelación y la resolución de problemas, con un 66,7% para el OA12 y un 62,5% respectivamente.

Al analizar la información de la Tabla 3, se destaca que, si bien no todas las actividades abordan las cuatro habilidades, los porcentajes son más altos en aquellas relacionadas con los objetivos de aprendizaje (OA) de probabilidad, en comparación con las asociadas a los OA de proporcionalidad, alcanzando su máximo porcentaje (44%) en la habilidad de resolución de problemas en primer año de Educación Media. Estos resultados evidencian un enfoque más destacado en el fomento de las habilidades en el ámbito de la probabilidad, en comparación con la proporcionalidad. Las actividades relacionadas con los OA de probabilidad, muestran una mayor atención y dedicación en la promoción de estas habilidades, lo cual se alinea con la importancia de desarrollar un razonamiento probabilístico sólido. Por otro lado, en las actividades asociadas a los OA de proporcionalidad, los porcentajes son más bajos, lo que sugiere que se les brinda menos énfasis y enfoque en el desarrollo de estas habilidades específicas. Es fundamental considerar estas diferencias al diseñar estrategias de enseñanza que promuevan, de manera equilibrada, el desarrollo de habilidades en ambos ámbitos.

La Figura 2 presenta un ejemplo de actividad diseñada para alcanzar el objetivo de aprendizaje OA18, que tiene como propósito desarrollar la habilidad de “argumentar y comunicar”. En esta actividad, los estudiantes al confeccionar la rueda de la fortuna, deberán ser capaces de identificar que los tamaños de los sectores del disco deben ser iguales, para garantizar la equiprobabilidad en el experimento. De igual forma, los estudiantes deberán realizar conjeturas sobre la ocurrencia de un evento basado en un experimento y determinar la frecuencia absoluta y relativa asociada a los colores de la rueda, utilizando herramientas como razones, fracciones o porcentajes para expresar y calcular la probabilidad.

 

Figura 2

Actividad para séptimo básico de probabilidad (MINEDUC, 2016, p.176)

 

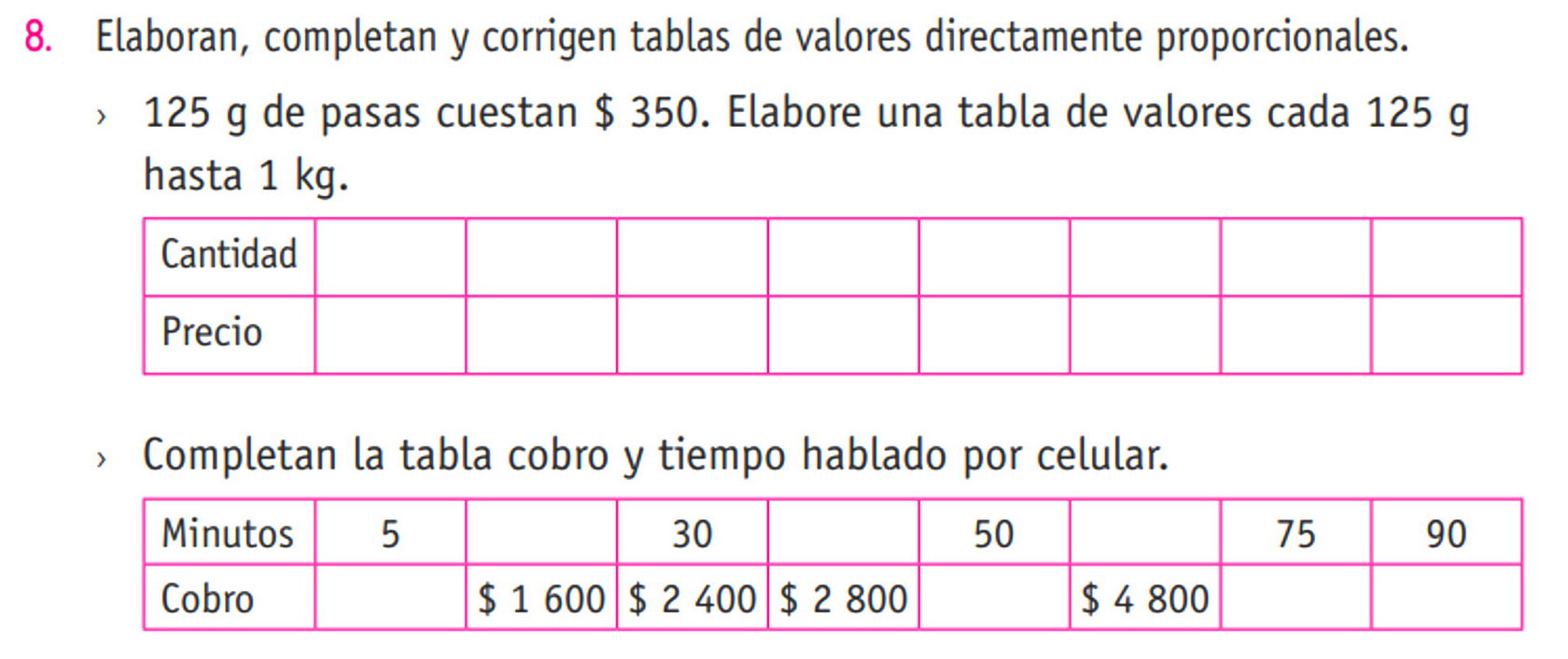
En relación al contenido de proporcionalidad, es relevante tener en cuenta que el Ministerio de Educación (MINEDUC) establece dos objetivos de aprendizaje específicos para este tema: uno para séptimo básico y otro para primero medio. A partir de la información recogida en la Tabla 3, se observa que, en el caso del OA8, el programa de estudios propone diez actividades que abarcan todas las habilidades necesarias. Estas actividades tienen como objetivo que los estudiantes resuelvan problemas utilizando las estrategias básicas de proporción, verifiquen los resultados obtenidos y evalúen los procedimientos utilizados. Un ejemplo claro de estas actividades es la Figura 3, que está específicamente diseñada para desarrollar la habilidad de “representación”, en la que se fomenta relacionar y contrastar información entre distintos niveles de representación. Esto implica que los estudiantes deben ser capaces de utilizar su comprensión sobre la proporcionalidad, para interpretar la información presentada.

En la actividad de la Figura 3, el estudiante debe elaborar una tabla de valores a partir de una situación-problema descrita, en la cual se establece una razón específica, como “350 pesos por cada 125 gramos” y, además, debe identificar la razón de proporcionalidad entre dos magnitudes que permite completar la tabla. De esta manera, los estudiantes deben traducir la información de una forma de representación a otra, y así profundizar su comprensión del concepto de proporcionalidad.

 

Figura 3

Actividad para séptimo básico de proporcionalidad (MINEDUC, 2016, p.115)

 

Con el fin de analizar la relación entre el razonamiento proporcional y el razonamiento probabilístico, se ha llevado a cabo una identificación de aquellas actividades relacionadas con los objetivos de aprendizaje (OA) de probabilidad que promueven el razonamiento proporcional. Estas actividades se distinguen por utilizar herramientas propias del razonamiento proporcional, como, por ejemplo, las razones o fracciones, para el cálculo o estimar de probabilidades. Por otro lado, en las actividades propuestas en los OA de proporcionalidad, se ha puesto especial atención en el contexto en el que se desarrollan estas. Se ha identificado si las actividades que requieren un razonamiento proporcional están enmarcadas en un contexto de la probabilidad.

Se ha observado que todas las actividades relacionadas con los objetivos de aprendizaje (OA) de proporcionalidad, carecen de un contexto probabilístico. No obstante, al analizar las actividades relacionadas con la probabilidad, se ha encontrado que la mayoría de ellas promueven el razonamiento proporcional, centrándose principalmente en el cálculo de frecuencias relativas a través de la realización de experimentos (véase Figura 2) o en el cálculo de la probabilidad utilizando la Regla de Laplace.

Al realizar un análisis por cursos, se ha identificado que, en séptimo básico, de las 12 actividades propuestas, ocho fomentan el uso del razonamiento proporcional. En octavo básico, este enfoque está presente en tan solo dos de las seis actividades. Por otro lado, en primero y segundo medio, más del 50% de las actividades incorporan el razonamiento proporcional, destacando un alto porcentaje en primero (75%). No obstante, en segundo medio, la presencia del razonamiento proporcional es menos notable (54.1%), debido a que las actividades se centran, de manera general, en la idea de variable aleatoria y combinatoria.

 

3.4. Proporcionalidad y probabilidad en la priorización curricular

 

La priorización curricular tiene como objetivo apoyar a las comunidades educativas en los procesos formativos de los estudiantes, en el contexto de emergencia sociosanitaria, priorizando, clasificando y promoviendo la integración de los distintos aprendizajes presentados en el currículo vigente. Esta priorización garantiza la presencia de los conceptos clave, así como de los principios disciplinarios y didácticos que sustentan el conocimiento, las habilidades y las actitudes propias de la materia, en nuestro caso, la matemática.

El documento se divide en tres bloques principales: los aprendizajes basales, corresponden a los OA que establecen las bases y fundamentos necesarios para el desarrollo de los planes educativos en cada materia, nivel y ciclo. Estos aprendizajes abarcan conocimientos clave, se relacionan con temas de relevancia social y promueven la integración con otros ámbitos de conocimiento. Los aprendizajes complementarios, se refieren a aquellos que no son considerados basales, pero tienen la finalidad de complementarlos y enriquecerlos, pudiendo ser integrados y/o articulados tanto dentro de las asignaturas como entre ellas, con el fin de alcanzar un aprendizaje completo en cada materia, nivel y ciclo. Los aprendizajes transversales se centran en los objetivos vinculados a los ámbitos de convivencia, bienestar, salud mental y formación ética de los estudiantes.

En cuanto a los objetivos de aprendizaje relacionados con probabilidad y proporcionalidad, enfocados en los niveles de séptimo a segundo medio, la Tabla 4 clasifica estos objetivos según su relevancia en el proceso de enseñanza y aprendizaje, distinguiendo entre aprendizajes basales y complementarios. Es relevante destacar que, aunque los objetivos de aprendizaje relacionados con la proporcionalidad establecidos en las bases curriculares son abordados en menor medida durante la etapa educativa, todos ellos son considerados aprendizajes basales. Esto puede deberse a que la adquisición de las proporciones directas e inversas permite al estudiante comprender y aplicar estos conceptos en situaciones cotidianas y académicas, como la resolución de problemas.

 

Tabla 4

Clasificación de los OA de proporcionalidad y probabilidad según tipo de aprendizaje

Curso	Unidad	OA	Eje	Tipo de aprendizaje
7º E.B.	2	8	Proporcionalidad	Basal
	4	18	Probabilidad	Basal
	4	19	Probabilidad	Complementario
8º E.B.	4	17	Probabilidad	Basal
1º E.M.	3	10	Geometría / Proporcionalidad	Basal
	4	14	Probabilidad	Basal
2º E.M.	4	10	Probabilidad	Complementario
	4	11	Probabilidad	Basal
	4	12	Probabilidad	Complementario

 

En relación al contenido de probabilidad, es posible observar que solamente se ha establecido un objetivo basal por curso, lo que implica que, en el caso de haber varios objetivos relacionados con la probabilidad en un mismo curso, sólo se considerará uno como fundamental. En el caso específico de séptimo curso de Educación Básica, el OA18 se establece como aprendizaje basal. Este objetivo se centra en explicar las probabilidades de eventos obtenidos a través de experimentos manuales o con software educativo, haciendo hincapié en un enfoque práctico. A través de esta aproximación, los estudiantes podrán desarrollar habilidades para estimar probabilidades de manera intuitiva, utilizando herramientas como frecuencias relativas, razones, fracciones o porcentajes. En el caso del OA19, se reconoce como un aprendizaje complementario, debido a que establecer la conexión entre el enfoque frecuencial y el enfoque teórico puede suponer una mayor complejidad para el nivel de séptimo curso.

En segundo medio, se produce una modificación significativa, quedando solo el OA11 como objetivo basal, centrado en la utilización de permutaciones y la combinatoria sencilla para calcular probabilidades de eventos y resolver problemas. Como resultado, otros objetivos importantes como OA10 y OA12 son considerados complementarios. Es particularmente sorprendente que el OA12, que se enfoca en el papel de la probabilidad en la sociedad y en cómo influye en las decisiones subjetivas o basadas en probabilidades, no sea considerado un aprendizaje fundamental. Diversos autores han manifestado que poseer un conocimiento de la probabilidad permite comprender y predecir mejor los fenómenos aleatorios presentes en nuestra vida y entorno (Batanero, 2006), además de mejorar la toma de decisiones en situaciones de incertidumbre (Gal, 2005).

El estudio realizado, demuestra la coherencia de mantener los objetivos de aprendizaje (OA) relacionados con la proporcionalidad como fundamentales, dado que tienen una influencia significativa en la adquisición de los aprendizajes basales asociados a la probabilidad.

 

4. REFLEXIONES FINALES

 

El razonamiento proporcional es una valiosa herramienta para capacitar la comprensión y aplicación de la probabilidad de manera efectiva, y la evaluación y equiparación de situaciones en contextos que involucren incertidumbre (Bryant y Nunes, 2012; Burgos et al., 2022; Vergara et al., 2020). Es importante tener en cuenta que numerosos estudios, han señalado que una deficiente capacidad de razonamiento proporcional puede ser una de las causas de errores en la interpretación y aplicación de procedimientos en el ámbito de la probabilidad (Begolli et al., 2021; Van Dooren, 2014). Por tanto, la comprensión de la proporcionalidad puede ser vista como un punto de partida fundamental para el desarrollo de habilidades en la resolución de problemas que impliquen probabilidades.

La inclusión de la enseñanza de la estadística y de la probabilidad en las bases curriculares de matemáticas, fue una de las reformas más significativas en la enseñanza de las matemáticas en Chile, y ha permitido que los estudiantes desarrollen habilidades en razonamiento probabilístico desde una edad temprana, lo que ha contribuido a mejorar su capacidad para enfrentar situaciones de la vida real que involucren estas áreas (Batanero, 2006). Considerando la importancia del pensamiento proporcional en el desarrollo del pensamiento probabilístico, resulta fundamental que el currículo educativo contemple objetivos y competencias relacionadas con ambas habilidades.

El presente estudio se enfocó en analizar la presencia de los contenidos de probabilidad y proporcionalidad en los cursos de séptimo a segundo medio, en el contexto del currículo educativo chileno. Los resultados del estudio indican que existe una escasa presencia de la enseñanza de la proporcionalidad, limitándose únicamente a dos objetivos de aprendizaje a lo largo de la etapa de Educación Media. Esto representa una brecha en el aprendizaje de los estudiantes, ya que, como afirman diversos autores, el razonamiento proporcional es fundamental para el desarrollo del pensamiento probabilístico. Además, se observa una falta de conexión entre los objetivos de aprendizaje de proporcionalidad y probabilidad en el currículo chileno, lo que podría generar dificultades en el aprendizaje efectivo de las matemáticas. Se evidencia que las actividades relacionadas con proporcionalidad, no están contextualizadas en situaciones probabilísticas, mientras que las actividades asociadas con probabilidad, requieren del uso del razonamiento proporcional. Por tanto, es necesario buscar una mayor integración entre ambos temas para fomentar un aprendizaje más integrado y efectivo de las matemáticas.

El estudio, también destaca que la enseñanza de la probabilidad en séptimo curso tiene un enfoque práctico que permite a los estudiantes desarrollar habilidades para estimar probabilidades intuitivamente y utilizando herramientas como frecuencias relativas, razones, fracciones o porcentajes. Sin embargo, en niveles educativos posteriores, se produce una reducción significativa de objetivos basales, lo que podría afectar negativamente el aprendizaje de los estudiantes en esta etapa educativa. En particular, la eliminación de objetivos importantes como OA10 y OA12, podría dificultar el desarrollo de habilidades esenciales en el ámbito de la probabilidad, como el cálculo de probabilidades de eventos complejos y la comprensión del papel de la probabilidad en la toma de decisiones cotidianas. Además, resulta llamativo que el OA12, que se enfoca en temas de gran relevancia social, no sea considerado un aprendizaje fundamental en este nivel educativo. Esto podría indicar una falta de énfasis en la importancia de la probabilidad en la vida cotidiana y en la toma de decisiones informadas. En general, estos resultados sugieren la necesidad de una revisión cuidadosa de los objetivos de aprendizaje en el área de la probabilidad en segundo medio y en otros niveles educativos, con el fin de asegurar un enfoque integral y efectivo de la alfabetización matemática en esta área.

A pesar de los esfuerzos realizados para mejorar el currículum educativo en Chile, los resultados muestran que todavía queda un largo camino por recorrer. Para garantizar una educación de calidad, que proporcione a los estudiantes las herramientas necesarias para enfrentar los desafíos del mundo actual y futuro, es fundamental seguir trabajando en la mejora del sistema educativo. Esto implica enfocarse en la centralización del aprendizaje, la integración de habilidades y actitudes en el conocimiento, así como en la mejora del enfoque disciplinario.

En consonancia con investigaciones previas, que han examinado las directrices curriculares de otros países (Batanero et al., 2014; Pino et al., 2014; Sánchez y Ruiz, 2020; Vergara, 2021), es importante destacar la relevancia de este tipo de análisis. En primer lugar, los hallazgos ponen de manifiesto la necesidad de fortalecer la enseñanza de la proporcionalidad en el currículo chileno, una habilidad fundamental para el aprendizaje de las matemáticas y, en particular, de la probabilidad. En segundo lugar, se subraya la importancia de que los docentes tengan acceso a información clara y útil sobre los objetivos de aprendizaje de las matemáticas en el currículo chileno. Este conocimiento les permitiría tomar decisiones informadas sobre cómo integrar los contenidos de probabilidad y proporcionalidad en su enseñanza, así como fomentar un aprendizaje más integrado y efectivo de las matemáticas. Por lo tanto, confiamos en que estos hallazgos sean útiles para los educadores en su labor de mejorar la calidad de la educación matemática, y para los responsables políticos al momento de tomar decisiones destinadas a fortalecer el sistema educativo en su conjunto. Con el compromiso y la colaboración de todos los actores del sistema educativo, podemos avanzar hacia una educación de calidad que prepare a nuestros estudiantes para el futuro.

 

Agradecimientos

Investigación realizada como parte del proyecto de investigación, PID2019-105601GB-I00/AEI/0.13039/501100011033, con apoyo del Grupo de Investigación FQM-126 (Junta de Andalucía, España).

 

REFERENCIAS BIBLIOGRÁFICAS

 

Batanero, C. (2006). Razonamiento probabilístico en la vida cotidiana: un desafío educativo. En P. Flores y J.L. Lupiáñez (Eds.), Investigación en el aula de matemáticas. Estadística y Azar (pp. 1-17). Sociedad de Educación Matemática Thales. https://n9.cl/q7v4p

Batanero, C., Arteaga, P. y Gea, M.M. (2012). El currículo de estadística: reflexiones desde una perspectiva internacional. UNO, 59, 9-17. https://n9.cl/q6zyl

Batanero, C., Gea, M.M., Arteaga, P. y Contreras, J.M. (2014). La estadística en la educación obligatoria: Análisis del currículo español. Revista digital Matemática, Educación e Internet, 14(2), 1-14. https://doi.org/10.18845/rdmei.v14i2.1663

Begolli, K.N., Dai, T., McGinn, K.M. y Booth, J.L. (2021). Could probability be out of proportion? Self-explanation and example-based practice help students with lower proportional reasoning skills learn probability. Instructional Science, 49, 441-473. https://doi.org/10.1007/s11251-021-09550-9

Bryant, P. y Nunes, T. (2012). Children’s understanding of probability: A literature review (full report). The Nuffield Foundation. https://n9.cl/ierqq

Burgos, M., López-Martín, M.M., Aguayo-Arriagada, C.G. y Albanese, V. (2022). Análisis cognitivo de tareas de comparación de probabilidades por futuro profesorado de Educación Primaria. Uniciencia, 36(1), 588-611. http://dx.doi.org/10.15359/ru.36-1.38

Cohen, L., Manion, L. y Morrison, K. (2007). Research methods in education. Routledge. https://doi.org/10.4324/9780203029053

Cox, C. (2011). Currículo escolar de Chile: génesis, implementación y desarrollo. Revue International de Education de Sevres, 56(1), 1-9. https://n9.cl/vu4vu

Dolores, C. (2012) ¿Hacia dónde reorientar el currículum de matemáticas del Bachillerato? En C. Dolores y M.S. García (Eds.), ¿Hacia dónde reorientar el currículum de matemáticas del Bachillerato? (pp. 118-133). Plaza y Valdez. https://n9.cl/cmyqp

Falk, R., Yudilevich-Assouline, P. y Elstein, A. (2012). Children’s concept of probability as inferred from their binary choices–revisited. Educational Studies in Mathematics, 81, 207-233. https://doi.org/10.1007/s10649-012-9402-1

Gal, I. (2005). Towards ‘probability literacy’ for all citizens. En G. Jones (Ed.), Exploring probability in school: Challenges for teaching and learning (pp. 43-71). Springer.

García-García, J.I., Carmona, J., Fernández, N.A. y Arredondo, E.H. (2022). Tendencias actuales en educación estadística. Aportaciones desde el Acta Latinoamericana de Matemática Educativa (2015- 2021). Revista de Educación Estadística, 1(1), 1-22. https://doi.org/10.29035/redes.1.1.8

Lamon, S. (2007). Rational number and proportional reasoning: toward a theoretical framework for research. En F.K. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp. 629-667). NCTM.

Merino, R.M. y Reyes, K.R. (2013). Comparación entre los contenidos del currículo chileno y español en el área de estadística y probabilidad. Probabilidad Condicionada: Revista de Didáctica de la Estadística, 2, 137-142.

MINEDUC. (2015). Bases curriculares Séptimo Básico a Segundo Medio. Unidad de Currículum y Evaluación.

MINEDUC. (2016). Programa de Estudio. Séptimo básico. Unidad de Currículum y Evaluación.

MINEDUC. (2018). Bases curriculares Primero a Sexto Básico. Unidad de Currículum y Evaluación.

MINEDUC. (2023). Actualización de la priorización curricular para la reactivación integral de aprendizajes. Unidad de Currículum y Evaluación.

OECD (2013). PISA 2012 Assessment and Analytical Framework: Mathematics, Reading, Science, Problem Solving and Financial Literacy. OECD Publishing. http://dx.doi.org/10.1787/9789264190511-en

OECD (2021). Governing Board: PISA 2021 Mathematics Framework (Second Draft). OECD Publishing.

Pino, C., Díaz-Levicoy, D. y Piñeiro, J.L. (2014). Los gráficos estadísticos como articuladores del currículo escolar. Revista chilena de Educación Científica, 13(2), 9-18.

Rodríguez, C. (2013) El potencial curricular de los libros de texto para generar experiencias de aprendizaje. Revista Educación, 37(1), 119-129.

Ruz-Fuenzalida, C. (2020). Construcción y trayectoria del currículum en Chile: una perspectiva desde las Nuevas Bases Curriculares para 3º y 4º medio. Revista Saberes Educativos, 4, 22-36. https://doi.org/10.5354/2452-5014.2020.55896

Salgado, A. (2007). Investigación cualitativa: diseños, evaluación del rigor metodológico y retos. Liberabit. Revista Peruana de Psicología, 13, 71-78.

Sánchez, N.A. y Ruiz, B.R. (2020). Análisis de las actividades propuestas en dos programas de estudio chilenos en el eje de Estadística y Probabilidad. IE Revista de Investigación Educativa de la REDIECH, 11, 1-24. https://doi.org/10.33010/ierierediech.v11i0.776

Van Dooren, W. (2014). Probabilistic thinking: analyses from a psychological perspective. En E. Chernoff y B. Sriraman (Eds.), Probabilistic Thinking. Advances in Mathematics Education (pp. 123-126). Springer.

Vásquez, C. y Alsina, Á. (2015) Conocimiento didáctico-matemático del profesorado de Educación Primaria sobre probabilidad: diseño, construcción y validación de un instrumento de evaluación. BOLEMA, 29(52), 681-703. https://doi.org/10.1590/1980-4415v29n52a13

Vásquez, C. y Alsina, Á. (2019). Diseño, construcción y validación de una pauta de observación de los significados de la probabilidad en el aula de educación primaria. REVEMAT: Revista Eletrônica de Educação Matemática, 14, 1-20.

Vásquez, C. y Cabrera, G. (2022). La estadística y la probabilidad en los currículos de matemáticas de Educación Infantil y Primaria de seis países representativos en el campo. Educación Matemática, 34(2), 245-274. https://doi.org/10.24844/EM3402.09

Velasco, K., Galindo, J. C. y Benítez, D. (2022). Un estudio sobre el razonamiento probabilístico de estudiantes de último año de bachillerato. Unión, 18(65), 1-22.

Vergara, M.I. (2021). Evaluando la presencia de las Bases Curriculares en Chile: diseño de una escala de Likert. Reaxion, Revista de Divulgación Científica, 9(1), 55-79.

Vergara, A., Estrella, S. y Vidal-Szabó, P. (2020). Relaciones entre pensamiento proporcional y pensamiento probabilístico en situaciones de toma de decisiones. Revista Latinoamericana de Investigación en Matemática Educativa, 23(1), 7-36. https://doi.org/10.12802/relime.20.2311

 

Como citar:

Aguayo-Arriagada, C.G, Ortiz, D. y López-Martín, M.M. (2022). La presencia del razonamiento proporcional y probabilístico en la enseñanza chilena: Un análisis de las normativas curriculares. Revista de Educación Estadística, 2(1), 1-21. https://doi.org/10.29035/redes.2.1.6

 

Esta obra está bajo una licencia de Creative Commons
Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional.