Revista de Educación Estadística https://revistaeduest.ucm.cl/ Vol. 2, n. 1, 1-25, abr. 2023 - sep. 2023 ISSN 2810-6164

 

DOI: https://doi.org/10.29035/redes.2.1.3

 

EXPLORANDO LA EXTENSIÓN DEL MODELO MTSK AL DOMINIO ESTADÍSTICO: CARACTERÍSTICAS DEL APRENDIZAJE DESDE LA TAXONOMÍA SOLO

Explorando a extensão do modelo MTSK ao domínio estatístico: características da aprendizagem com a Taxonomia SOLO

Exploring the extension of the MTSK model to the statistical domain: features of learning from SOLO Taxonomy

Pedro Vidal-Szabó*1

Universidad del Desarrollo (Santiago, Chile)

Soledad Estrella2

Pontificia Universidad Católica de Valparaíso (Valparaíso, Chile)

 

Resumen

La investigación buscó ampliar la comprensión sobre la extensión del modelo MTSK —Conocimiento Especializado del Profesor de Matemáticas— a la disciplina Estadística, nombrado modelo STSK (i. e., Statistics Teacher´s Specialized Knowledge). Se exploraron los conocimientos didácticos del contenido y niveles de comprensión manifestados por 192 docentes, sobre las dificultades que podrían expresar estudiantes de educación básica al interpretar una representación de datos tabulados. Mediante un enfoque cualitativo y en base a la taxonomía SOLO, se clasificaron 384 respuestas escritas a dos ítems de un cuestionario aplicado en línea y validado por juicio de 15 expertos. Los resultados muestran que solo un 36% de las respuestas docentes están en los niveles superiores de la taxonomía SOLO, y manifiestan un conocimiento especializado en el subdominio de conocimiento de las características del aprendizaje estadístico. El estudio aporta al conocimiento teórico especializado vinculado con la formación docente en estadística temprana, al caracterizar cierto conocimiento didáctico del contenido del profesorado, mediante categorías y descripciones propuestas y evidenciadas del subdominio conocimiento de las características del aprendizaje de la estadística del modelo STSK.

Palabras clave: Estadística Temprana, Modelo STSK, conocimiento didáctico del contenido (PCK), subdominio KFSL

 

Resumo

A investigação procurou alargar a compreensão da extensão do modelo MTSK à disciplina de estatística, referida como o modelo STSK (isto é, Conhecimento Especializado do Professor de Estatística). Explorámos os conhecimentos de conteúdo didáctico e os níveis de compreensão expressos por 192 professores sobre as dificuldades que os alunos do ensino básico poderiam expressar ao interpretar uma representação dos dados tabulados. Utilizando uma abordagem qualitativa e com base na taxonomia SOLO, 384 respostas escritas a dois itens de um questionário em linha foram classificadas e validadas pelo julgamento de 15 peritos. Os resultados mostram que apenas 36% das respostas dos professores se encontram nos níveis superiores da taxonomia SOLO, e manifestam conhecimentos especializados no subdomínio do conhecimento das características de aprendizagem estatística. O estudo contribui para o conhecimento teórico especializado ligado à formação inicial de professores de estatística através da caracterização de alguns conhecimentos de conteúdo didáctico de professores através de categorias propostas e comprovadas e descrições do subdomínio conhecimento de características de aprendizagem estatística do modelo STSK.

Palavras-chave: Estatísticas iniciais, modelo STSK, conhecimento pedagógico do conteúdo (PCK), subdomínio KFSL

 

Abstract

The research sought to broaden understanding of the extension of the MTSK model to the discipline of statistics, referred to as the STSK model (i.e., Statistics Teacher’s Specialized Knowledge). We explored the didactic content knowledge and levels of understanding expressed by 192 teachers about the difficulties that elementary school students might express when interpreting a representation of tabulated data. Using a qualitative approach and based on the SOLO taxonomy, 384 written responses to two items of an online questionnaire were classified and validated by the judgement of 15 experts. The results show that only 36% of the teacher responses are in the upper levels of the SOLO taxonomy, and manifest specialised knowledge in the subdomain of knowledge of the features of learning statistics. The study contributes to the specialised theoretical knowledge linked to early statistics teacher education by characterising some didactic content knowledge of teachers through proposed and evidenced categories and descriptions of the subdomain knowledge of the features of learning statistics of the STSK model.

Keywords: Early Statistics, STSK model, pedagogical content knowledge (PCK), KFSL subdomain

 

Recibido: 07/02/2023 - Aceptado: 01/05/2023

 

1. INTRODUCCIÓN

 

La estadística es una disciplina científica autónoma y, por ende, no es una rama de la matemática (cf., Wild et al., 2018). A pesar de ello, algunos profesores siguen concibiendo los contenidos estadísticos como si fueran parte de la matemática, no reconociendo que la estadística tiene sus ideas fundamentales (e.g., Ben-Zvi y Garfield, 2004; Moore, 1997). Además, en el transcurso de la modelación estadística hay que destacar que tanto la matemática como la computación son consideradas herramientas auxiliares en la comunidad de educación estadística (Pfannkuch, 2011). En ese sentido, parece necesario que el profesorado que enseña estadística reconozca el trabajo estadístico y valore el razonamiento con datos reales en contextos diversos y en escenarios con incertidumbre (Cobb y Moore, 1997; Estrella, 2018; Estrella et al., 2022; Estrella y Vidal-Szabó, 2017; Pfannkuch y Wild, 2000).

Wild et al. (2018), plantean como desafío de la enseñanza de la estadística, la toma de conciencia sobre cómo una variedad de contextos que portan los datos, puede permitir caracterizar el pensamiento estadístico que desarrollan los estudiantes, dándoles acceso a convertir los datos en visiones del mundo real, como había sido investigado empíricamente por Wild y Pfannkuch (1999) en su marco tetradimensional para el pensamiento estadístico. Así, la estadística no se desarrolla lejos de los problemas reales, lo que supone una integración del conocimiento contextual al trabajo estadístico (del Pino y Estrella, 2012). Epistemológicamente, el contexto da cuenta de la situación del mundo real de la cual provienen los datos y, cognitivamente, el contexto se sitúa en el aprendizaje y la experiencia del sujeto que se desempeña estadísticamente; por tanto, ambas perspectivas sobre el contexto se vinculan en el espacio de trabajo estadístico de las personas o de las instituciones educativas (Pfannkuch, 2011; Vidal-Szabó et al., 2020).

Es relevante precisar el trabajo estadístico de los estudiantes y examinar sus posibles rutas de aprendizaje, incluyendo fortalezas y dificultades en el proceso educativo. Por ejemplo, Ben-Zvi y Garfield (2004) advierten que los estudiantes vinculan procedimentalmente la estadística con la matemática, y se enfocan en calcular números, ocupar fórmulas y otorgar una única respuesta correcta, por lo que sienten cierta incomodidad con el desorden de los datos, las diferentes interpretaciones posibles en función de diferentes supuestos, y el uso de escritura y habilidades de comunicación para dar cuenta del comportamiento de los datos. Al respecto, el abordaje educativo del trabajo estadístico puede estar siendo insuficiente en el currículo impartido, si no son consideradas en la enseñanza actividades como el diseño de recolección de datos, el análisis exploratorio de los mismos y su interpretación en contextos diversos, mediante distintos formatos representacionales de datos (e.g., English, 2010, 2012, 2018; Estrella, 2017; Vidal-Szabó, 2021), las que son fundamentales para el desarrollo temprano del pensamiento estadístico (e.g., Estrella, 2018; Estrella et al., 2018; Estrella et al., 2023).

El conocimiento estadístico para la enseñanza no es idéntico al conocimiento de la estadística como disciplina, ya que los conocimientos de profesores sobre cómo hacer que los contenidos estadísticos sean comprensibles durante sus enseñanzas, difieren de los conocimientos estadísticos que manifiestan sobre dichos contenidos (Groth, 2017). El modelo SKT –i.e., conocimiento para la enseñanza de la estadística de Groth y Bergner (2013)– tiene por premisa que los docentes necesitan conocimientos específicos del contenido estadístico para guiar la enseñanza, empleando de base el modelo MKT –i.e., Mathematical Knowledge for Teaching de Ball et al. (2008)– para identificar elementos de conocimiento relevantes para SKT. El modelo SKT combina conocimientos de la materia y del contenido pedagógico de los profesores (Groth, 2017). Sin embargo, al igual que el modelo MKT, el modelo SKT es todavía impreciso de acuerdo con algunos elementos particulares que son o no exclusivos de los profesores que enseñan estadística, siendo posible una superposición de los subdominios, en palabras del autor:

Al igual que con todas las categorías de conocimiento analizadas hasta ahora, cabe señalar que estas tres categorías se solapan en cierta medida con otras. Por ejemplo, tanto el conocimiento especializado como el conocimiento del contenido y la enseñanza implican hacer que la materia sea comprensible para los estudiantes. Además, tanto el conocimiento del contenido y la enseñanza como el conocimiento del currículo implican el uso de estrategias específicas para facilitar el aprendizaje de los estudiantes. Los ejemplos anteriores de la literatura sobre educación estadística proporcionan cierta orientación para distinguir entre las categorías de conocimiento, pero sin duda aún dejan espacio para la ambigüedad. (Groth, 2017, p. 10)

Por otra parte, existe interés en realizar adaptaciones al modelo de Conocimiento Especializado del Profesor de Matemática (modelo MTSK) para caracterizar y examinar el conocimiento especializado de profesores de otras disciplinas, en ese sentido, la extensión de este modelo se ha denominado modelo XTSK en que “X” hace alusión a diferentes disciplinas científicas, sociales o lingüísticas. En especial, Conocimiento Especializado del Profesor de Biología (modelo BTSK), del Profesor de Química (modelo QTSK), entre otros (Codes et al., 2020).

A partir del modelo MTSK, se ha estado levantando un marco referencial para la educación estadística con fines de desarrollo profesional docente, denominado modelo STSK –i.e., Statistics Teacher’s Specialized Knowledge–, teniendo en cuenta que la educación estadística como disciplina ha adquirido autonomía e independencia de la didáctica de la matemática o de la matemática educativa (Zieffler et al., 2018), y que existen intentos teóricos de algunos investigadores por mapear el conocimiento estadístico para la enseñanza (cf., Groth, 2007, 2017; Groth y Bergner, 2013), todavía incipientes para caracterizar el conocimiento especializado del profesor de estadística en enseñanza básica.

El presente estudio exploratorio busca caracterizar los conocimientos y niveles de comprensión que expresan profesores que enseñan estadística en educación básica referido a las características del aprendizaje de la estadística de los estudiantes. A razón de ello, se examina un subconjunto de 384 respuestas que dieron los docentes a un cuestionario en línea, a través de la taxonomía SOLO, para caracterizar y ejemplificar el conocimiento sobre las características del aprendizaje de la estadística.

 

2. MARCO CONCEPTUAL

 

El modelo de Conocimiento Especializado del Profesor de Matemática –MTSK, Mathematics Teacher´s Specialized Knowledge– permite examinar de forma analítica las especificidades del conocimiento que manifiesta el profesorado, en su actuar profesional, al enseñar matemática (Carrillo et al., 2013; Flores et al., 2013). Este modelo particulariza el conocimiento especializado del profesor de matemática en dominios del conocimiento matemático (MK, Mathematical Knowledge) y del conocimiento didáctico del contenido (PCK, Pedagogical Content Knowledge), además considera las creencias sobre dichos dominios.

El modelo MTSK considera el dominio MK como un conocimiento disciplinar científico propio del campo matemático enmarcado en la educación, mientras que el dominio PCK abarca los contenidos matemáticos en virtud de los procesos de enseñanza, evaluación y aprendizaje propios de la formación estudiantil en diversos niveles educativos (Carrillo et al. 2018). En contraste con el modelo MKT
–Mathematical Knowledge for Teaching (Ball et al., 2008)–, el modelo MTSK acentúa la conceptualización sobre la especialización del conocimiento del profesor de matemática como un agente educativo profesional, lo que implicó reconfigurar el conocimiento matemático (MK) y reinterpretar el conocimiento didáctico del contenido (PCK). La noción de especialización, según Scheiner et al. (2019), es inabordable si sólo se toma en cuenta lo que sabe el profesorado que enseña matemática, pues también es esperable que se consideren las producciones de conocimiento que genera tanto en su actuar profesional como durante su formación.

Dado que la estadística es una disciplina científica, no siendo una rama de la matemática (Cobb y Moore, 1997), y que la educación estadística ha cobrado cada vez más importancia y desarrollo, diferenciándose de la educación matemática (Zieffler et al., 2018); entonces, resulta indebido tomar el modelo MTSK para caracterizar o examinar el conocimiento especializado del profesor que enseña estadística. En ese sentido, Vidal-Szabó y Estrella (2020) proponen inéditamente la extensión del modelo MTSK a la estadística, bajo la denominación modelo STSK –i.e., Statistics Teacher´s Specialized Knowledge– el cual, en adelante, sigue siendo precisado en estudios recientes (e.g., Seguí y Alsina, 2022; Vidal-Szabó, 2022; Vidal-Szabó y Estrella, 2021).

La hipótesis de trabajo del modelo STSK es la existencia de un rol dual y complejo del profesor que enseña en la asignatura matemática, en tanto, trata contenidos matemáticos y estadísticos en dicha asignatura (Vidal-Szabó y Estrella, 2020). Por ello, el término profesor de estadística es concebido como el profesor de matemática que enseña estadística, lo que es usual en los sistemas escolares (e.g., Australian Curriculum, Assessment and Reporting Authority, 2013; Common Core State Standards Initiative, 2017; Ministerio de Educación de Chile, 2012; New Zealand Ministry of Education, 2007). También, por conocimiento especializado en el modelo STSK, se concibe todo conocimiento que requiere el profesorado para enseñar estadística, excluyéndose tanto los conocimientos vinculados con la pedagogía general como los conocimientos de otros profesionales que emplean la estadística en sus campos laborales y que no sean educativos (Vidal-Szabó y Estrella, 2021). Análogo al modelo MTSK, en el modelo STSK se considera el conocimiento estadístico y el conocimiento didáctico del contenido, propios del profesor de estadística, además de las creencias asociadas a dichos dominios de conocimiento.

En el dominio conocimiento didáctico del contenido del modelo STSK, existe un subdominio referido al conocimiento sobre las características del aprendizaje de la estadística (KFSL; Knowledge of Features of Statistic Learning). Este subdominio es base para comprender cómo piensan y construyen los estudiantes el conocimiento estadístico al resolver cierto problema que requiere de datos para resolverse, abarcando ventajas y dificultades que pueden presentar las características de cada aspecto de un contenido estadístico, sujeto al aprendizaje de los estudiantes (Vidal-Szabó y Estrella, 2020). Tal como indican Seguí y Alsina (2022), el KFSL involucra el proceso de comprensión de los estudiantes sobre los distintos contenidos —así como errores, dificultades u obstáculos posibles en el proceso de aprendizaje— y, además, considera el lenguaje que ocupan los estudiantes, asociado a cada concepto estadístico y relacionado con las características del aprendizaje derivadas de su interacción con dicho contenido. La Tabla 1 exhibe una propuesta de categorías y descripciones para el subdominio KFSL, con base en el modelo MTSK (cf., Carrillo et al., 2018) y la literatura disponible en educación estadística (e.g., English, 2010, 2012, 2018; Estrella et al., 2018; Vidal-Szabó et al., 2020; Vidal-Szabó, 2021).

 

Tabla 1

Categorías y descripciones en relación con el KFSL del profesorado

Categoría	Descripción	Ejemplo
A) Fortalezas y debilidades en el aprendizaje de la estadística.	Se relaciona con los estilos de aprender y las distintas maneras de entender los rasgos sustanciales de los contenidos estadísticos por parte de los estudiantes, esto es, conocimientos sobre el origen de la dificultad en los estudiantes para cierto contenido, o bien, fortalezas que muestran durante el aprendizaje de cierto contenido estadístico.	Obviar la clave en un pictograma para interpretar los datos, tal como lo reporta la Agencia de Calidad de la Educación (2019, p. 38).
B) Tipos de interacción de los estudiantes con el contenido estadístico.	Los procedimientos y estrategias, convencionales o no convencionales, que emplean los estudiantes para desarrollar actividades estadísticas, así también el uso que hacen los estudiantes de ciertos términos, no necesariamente estadísticos per se, para comunicar alguna idea que contribuye a interactuar con el contenido estadístico. Lo anterior, es un conocimiento que el profesor de estadística desarrolla para poder interpretar el desempeño de sus estudiantes.	Tener en cuenta cómo las diversas estrategias de conteo de los estudiantes pueden facilitar o no la obtención de la frecuencia absoluta tal como lo reportan Estrella et al. (2018, p. 146).

 

3. METODOLOGÍA

 

Este estudio cualitativo y exploratorio pretende dar evidencias del conocimiento especializado, relacionado con las características del aprendizaje de la estadística de los estudiantes, en profesores que se desempeñan en educación básica.

 

3.1. Participantes y contexto

 

La muestra recogida es no-probabilística, por conveniencia y heterogénea, contempló a 192 profesores que realizan clases de estadística en la asignatura matemática desde 1° a 6° año básico, cuya edad modal de niñas y niños fluctúa entre los 6 a 11 años, en dicho tramo educativo en escuelas chilenas. El 88% de los participantes son profesores de educación básica y el 12% son de educación diferencial (o educación especial); 133 profesores trabajan en establecimientos educativos de tipo municipal, 50 en particulares subvencionados y 9 en privados; y declaran que donde más han trabajado en Chile es en la zona centro (desde la región de Valparaíso hasta la del Maule) con un total de 126 docentes, 41 en la zona norte (desde la región de Arica y Parinacota hasta la de Coquimbo) y 25 en la zona sur (desde la región de Ñuble hasta la de Magallanes y de la Antártica chilena).

El año 2020, dichos profesores contestaron un cuestionario en línea y de acuerdo con el orden temporal de envío de sus respuestas a Google Forms, se les asignó un único código de identificación a cada uno, desde P001 hasta P192; todos otorgaron autorización para el uso de sus respuestas, garantizando anonimato y bajo circulación reservada para fines de investigación.

 

3.2. Proceso de validación del instrumento de recogida de datos

 

El instrumento de recogida de datos fue sometido al método por juicio experto, permitiendo una validación y refinamiento de este, vía Google Forms. Al respecto, el método escogido solicita a personas un juicio hacia un instrumento y su opinión de acuerdo con algún aspecto específico, lo cual es útil para la valoración netamente cualitativa; asimismo, es un indicador de validez de contenido su adecuada aplicación (Escobar y Cuervo, 2008). Este método permitió dar fiabilidad al instrumento, al considerar opiniones informadas de 15 personas expertas en el área, quienes fueron seleccionadas por acumular una trayectoria adecuada y pertinente en el rol de juez experto, en tanto poseen experiencia y/o formación situada en educación básica.

Los jueces expertos en cada uno de los ítems evaluados, llevaron a cabo dos acciones específicas, a saber, (i) mediante una escala discreta desde 0 hasta 5, evaluaron qué tan comprensibles fueron los elementos contenidos en cada ítem para un docente; también qué tan precisos eran los conceptos utilizados en cada ítem, evitando ambigüedades; y finalmente qué tan pertinente era el objetivo de cada ítem y las eventuales respuestas al mismo; y (ii) mejoraron el ítem, según recomendaciones para ganar comprensión, precisión y/o pertinencia, en la sección “observaciones o sugerencias”.

Luego, el cuestionario se reformuló vía Google Forms en su versión final, tras la realización del método de validación y la examinación del grado de acuerdo de todos los jueces participantes, sobre la base de las acciones descritas anteriormente en (i) y (ii). Tal como reportaron Vidal-Szabó y Estrella (2021), esta herramienta en línea permitió aplicar 24 ítems con formatos de respuesta tales como varias opciones (42,3% ítems de selección única), casillas (11,5% ítems de selección múltiple), párrafo (30,8% ítems de respuesta escrita) y escala lineal (15,4% ítems de valoración). El cuestionario consta de secciones agrupadas: (a) consentimiento informado (sección 1); (b) información sobre su perfil profesional (sección 2 a la 10); (c) la estadística y su enseñanza (sección 11 a la 23); (d) interpretación gráfica (sección 24 a la 28); (e) representaciones de datos en educación básica (sección 29 a la 33), y (f) reflexiones finales y contacto (sección 34 a la 37).

Para efectos de este artículo, el análisis de las respuestas se enfoca en los ítems 20 y 21, cuyo formato es de respuesta escrita y referidos a la identificación de dos posibles dificultades que podría presentar algún estudiante de educación básica en 1° y 2° año básico, respectivamente. Además, estos ítems tuvieron un grado de acuerdo, mayormente, sobre 4 en la acción (i) como se puede apreciar en la Tabla 2 y hubo modificaciones a estos ítems por la acción (ii) como se puede apreciar en el anexo 1.

 

Tabla 2

Resultados de la evaluación sobre el grado de comprensión, precisión y pertinencia de los ítems 20 y 21 del cuestionario

Ítem	Criterios de evaluación	Escala semántica diferencial
		0	1	2	3	4	5
20	comprensión	0%	6.7%	0%	0%	13.3%	80%
	precisión	0%	6.7%	6.7%	0%	13.3%	73.3%
	pertinencia	0%	6.7%	0%	0%	6.7%	86.7%
21	comprensión	0%	0%	0%	0%	14.3%	85.7%
	precisión	0%	6.7%	0%	6.7%	13.3%	73.3%
	pertinencia	0%	6.7%	0%	0%	6.7%	86.7%

Nota. La escala semántica diferencial ocupada abarca desde 0 a 5 puntos, discretamente. En particular, para el grado de comprensión desde 0: nada comprensible, hasta 5: totalmente comprensible; para el grado de precisión desde 0: nada de precisa, hasta 5: totalmente precisa; para el grado de pertinencia desde 0 nada de pertinente, hasta 5: totalmente pertinente.

 

3.3. Procedimiento de análisis de las respuestas al cuestionario

 

La taxonomía SOLO –i.e., Structure of Observed Learning Outcome– de Biggs y Collis (1989), da cuenta del incremento de la complejidad en el desempeño vinculado con tareas de aprendizaje, de modo que una respuesta es considerada un resultado de aprendizaje que puede observarse, la cual es provocada por una pregunta (o tarea). Esta taxonomía brinda un enfoque para categorizar el rendimiento cognitivo, teniendo en cuenta la estructura del resultado de aprendizaje observado. Nótese que el grado de complejidad en la respuesta depende tanto de la capacidad cognitiva del individuo como de la dificultad de la pregunta.

La taxonomía SOLO contiene cinco niveles ascendentes que, a continuación, se describen a partir de Estrella et al. (2019) y Chick (1998):

Preestructural (PE), es el nivel más bajo, la respuesta da cuenta que el individuo no ha captado la pregunta. En otras palabras, se utiliza un dato o proceso incorrecto de forma simplista que puede llevar a una conclusión irrelevante. El individuo puede incluso no comprometerse con el problema, por lo que no hay ningún tipo de cierre en la respuesta.

Uniestructural (UE), es el nivel en que la respuesta dada a la pregunta atiende a solo una parte de la tarea. Un único proceso o concepto se aplica, al menos, a un dato. Se extrae una conclusión, pero a menos que el proceso único junto con los datos seleccionados sean suficientes para la correcta solución del problema, la conclusión no será válida del todo.

Multiestructural (ME), es el nivel en que la respuesta tiene una descripción cualitativa de la situación. Se utiliza una serie de procesos o conceptos sobre uno o más datos, pero sin síntesis de la información ni conclusiones intermedias. Esta falta de síntesis puede ser aceptable en el caso de una pregunta sencilla, o puede indicar un rendimiento cognitivo inferior que se requiere para resolver el problema con éxito.

Relacional (R), es el nivel en que la respuesta integra la descripción cualitativa con un aspecto cuantitativo. Una respuesta relacional se caracteriza por la síntesis de información, procesos y resultados intermedios. Para llegar a la conclusión, se aplican conceptos a algunos de los datos, dando resultados intermedios que luego se relacionan con otros datos y/o procesos.

Abstracto ampliado (A+) es el nivel más alto en que las respuestas abstractas ampliadas son estructuralmente similares a las respuestas relacionales, pero en este caso los datos, conceptos y/o procesos (más habitualmente los dos últimos), se extraen de fuera del dominio de conocimiento y experiencia que se supone, hipotéticamente, en la pregunta.

Las respuestas a los ítems considerados fueron sometidas a un proceso de clasificación por medio de la taxonomía SOLO, puesto que permite examinar las respuestas por nivel para describirlas y caracterizarlas de acuerdo con la manifestación de algún conocimiento sobre las características del aprendizaje de la estadística. Dicho proceso constó de dos etapas, en la primera, uno de los investigadores (del presente estudio) clasificó las 384 respuestas totales provenientes de los ítems 20 y 21 con la taxonomía SOLO. Luego, en la segunda etapa, conjuntamente los dos investigadores examinaron cada una de las respuestas clasificadas, según los niveles jerarquizados (i.e., respuestas clasificadas como PE, UE, ME, R, A+), ratificando la mayoría y, en menor medida, consensuando las discrepancias.

 

3.4. Respuestas esperadas al ítem 20 y 21

 

A partir del análisis de las tareas contenidas en los ítems 20 y 21, se definieron ciertas respuestas esperadas como análisis previo, fundamentado en algunos estudios previos (e.g., Estrella, 2018; Estrella et al., 2018; Vidal-Szabó, 2021). En particular, como respuesta esperada al ítem 20 se pueden identificar las siguientes dificultades que podrían tener los estudiantes de 1° año básico al interpretar la Figura 1, a continuación.

 

Figura 1

Representación de datos tabulados del ítem 20

- El uso de distintos íconos puede dificultar la lectura tabular porque la dimensionalidad de los íconos no se conserva. Por ejemplo, la cantidad de estudiantes que prefieren plátano y los que prefieren manzana es la misma (frecuencia absoluta 4, si se considera que la clave de cada ícono corresponde a la preferencia de solo 1 estudiante) aunque visualmente la cantidad de estudiantes que prefieren plátano se aprecie mayor a los que prefieren manzana, dada la dimensionalidad de sus íconos.

- En ausencia del total de estudiantes del grupo encuestado para obtener los datos tabulados, el número de estudiantes que prefieren guinda es poco clara, pues el ícono muestra agrupaciones que tienen dos guindas, lo que hace cuestionable si acaso semióticamente un par de guindas es la preferencia de un estudiante, o bien, de dos estudiantes. Por tanto, la frecuencia absoluta está indeterminada.

- La elección de tres íconos para representar la preferencia de las frutas (plátano, manzana y guinda), puede omitir a la variable frutas preferidas de un grupo de estudiantes por otra que tenga relación con la cantidad de frutas, prescindiendo de la preferencia y desvirtuando el contexto de los datos.

Mientras que para el ítem 21, como respuesta esperada vinculada a las posibles dificultades que podrían tener estudiantes de 2° año básico al interpretar la Figura 2, se describen a continuación.

 

Figura 2

Representación de datos tabulados del ítem 21

- El uso del ícono bicicleta completo y su mitad puede dificultar la lectura porque la mitad de una bicicleta no se condice con el contexto de venta de bicicletas; por tanto, es requerido un grado de abstracción mayor. Especialmente, interpretar que la mitad del ícono bicicleta es un medio de la cantidad de bicicletas vendidas que representa el ícono completo.

- La consideración de dos claves, esto es, la cantidad de bicicletas vendidas que representa el ícono completo y su mitad puede entorpecer la determinación de la frecuencia absoluta. También la omisión de las claves puede provocar una interpretación inadecuada.

- La interpretación de las ventas de bicicletas en los meses de enero y abril podría verse afectada por el uso del ícono bicicleta a su mitad y/o considerar equivocadamente que un ícono de bicicleta representa la venta de una bicicleta para los meses febrero, marzo, mayo y junio, omitiendo la clave.

- El total de bicicletas vendidas excede el ámbito numérico que habitualmente se trabaja en 2° año básico que llega hasta 1000. Notar que la frecuencia máxima es de 500 bicicletas vendidas en mayo.

Para efectos de la operacionalización de la Taxonomía SOLO en la clasificación de las 384 respuestas, la Tabla 3 sintetiza la caracterización de las respuestas en cada nivel. Luego, se identifican evidencias de la manifestación del KFSL –en las categorías a y b que exhibe la Tabla 1– y considerando la clasificación de respuestas a los ítems 20 y 21 en los niveles ME, R y A+.

 

Tabla 3

Caracterización de las respuestas al ítem 20 y 21, según taxonomía SOLO

	Niveles de la taxonomía SOLO
	PE	UE	ME	R	A+
Descripción	No identifica ninguna dificultad o responde incorrectamente	Identifica solo una dificultad que podría tener algún estudiante frente a la interpretación de una representación de datos	Identifica dos o más dificultades que podría tener algún estudiante frente a la interpretación de una representación de datos	Identifica dos dificultades que podría tener algún estudiante y da fundamentos sobre esta, frente a la interpretación de una representación de datos	Identifica más de dos dificultades que podría tener algún estudiante y da fundamentos sobre esta, frente a la interpretación de una representación de datos

 

4. ANÁLISIS Y RESULTADOS

 

En seguida, se exhiben las respuestas clasificadas por ítem en concordancia con la taxonomía SOLO. Después, se examinan evidencias en el profesorado participante, respecto a la manifestación del KFSL.

 

4.1. Análisis de las respuestas al ítem 20

 

Para la consigna: un objetivo de aprendizaje para 1° año básico es “construir, leer e interpretar pictogramas”. Indique brevemente dos dificultades que podría tener algún estudiante para interpretar estadísticamente la siguiente representación de datos (ver Figura 1); las 192 respuestas al ítem 20 se clasificaron según la descripción propuesta, concordante a la taxonomía SOLO (ver Tabla 4).

 

Tabla 4

Distribución de las respuestas al ítem 20 relacionado a las posibles dificultades que pueden presentar estudiantes al interpretar una representación de datos, según taxonomía SOLO

Nivel SOLO	Frecuencia	Respuestas ilustrativas
PE	20 (10.42%)	P027. Interpretación y lectura. P082. Todas tienen la misma cantidad. P107. Puede confundirse porque todos tienen la misma cantidad, puede pensar que siempre los datos serán iguales. P125. Dificultad de aprendizaje, dificultad de concentración
UE	88 (45.83%)	P016. El conteo de 2 en 2 de las guindas puede contar de 1 en 1 P021. No sale explicitado el valor de cada dibujo. P040. Aunque están las representaciones falta saber la cantidad de niños y niñas que los prefieren. P087. En las guindas, las puede contar por separado (8) o por conjunto (4). P102. Asignar valores a los dibujos P105. El tamaño de los dibujos, porque finalmente son la misma cantidad, pero varía el tamaño. P119. No sale el valor que tiene cada fruta, es decir, qué representa cada una (un niño, dos, tres, cuatro, etc.) P162. El tamaño del dibujo de las frutas debiese ser el mismo. P188. Los tamaños de las frutas
ME	68 (35.42%)	P034. El tamaño de las representaciones: Pensar que el plátano es más preferido porque es más grande que el resto de las frutas. Confundir la guinda con dos frutas. P065. Las guindas las puede contar dobles. Podría agrupar por colores y confundir manzanas y guindas. P106. El tamaño de las frutas, el no haber separado visualmente los espacios entre fruta y fruta de la misma variedad, o haber acompañado con un número, [...]”. P114. Las frutas tendrían que ser del mismo tamaño para mejor conteo (guinda es muy pequeña) y también deben estar separadas (guindas unidas). P135. (1) Contar cada guinda como dos unidades; (2) Dejarse llevar por el tamaño de las imágenes representadas. P191. El tamaño de cada fruta debería ser idéntico para todos. La distribución de espacio debería ser idéntica.
R	11 (5.73%)	P063. Una dificultad sería que no se coloca la misma representación pictórica, colocaría a un niño/a, ya que es la preferencia de ellos. La segunda dificultad seria es que son de diferente tamaño y esto puede generar un error en los estudiantes al analizarlos. P080. (1) Al ser de diferentes tamaños las frutas, podría interpretar que la fruta preferida de los estudiantes son los plátanos; (2) Podría contar cada grano de la guinda e interpretar que esa es la fruta favorita, al contar 8. P095. Por el tamaño de las frutas, se verán menos guindas por ser más pequeñas. La representación de las guindas, ya que el niño contará ocho no cuatro. P170. Cada guinda se considera como unidad o como dos unidades visualmente, también podría decir que hay menos cantidad por lo pequeño de la imagen. Por otro lado, un niño o niña podría decir que hay más plátanos por el tamaño, ya que visualmente se “ve más”
A+	5 (2.60%)	P044. En primer lugar, el hecho de utilizar guindas unidas de a par no especifica si cada par representa la opinión de uno o de dos alumnos. En segundo lugar, al utilizar texto en las categorías, se debería colocar el dibujo de la fruta en lugar del nombre de la categoría y representar la cantidad de alumnos que las prefieren con líneas o círculos para indicar la cantidad de cada una de ellas. P094. En los plátanos y manzanas, visualmente, se destaca muy bien la cantidad; sin embargo, en las guindas podría confundirse entre cantidad de “racimos” y cantidad total de guindas. Podría decir: “Hay 4 guindas” o “hay 8 guindas”. Otra dificultad es que podría considerar que prefieren más plátanos porque visualmente, la imagen de ellos es más larga en su extensión. P111. A que se refiere la cantidad de frutas dibujadas, no entenderían los nombres de las frutas, se podría colocar la imagen de la fruta y con rayitas la cantidad de niños que las prefieren.

Nota. Las respuestas seleccionadas para cada nivel de la taxonomía SOLO son ilustrativas, no pretenden ser representativas del nivel. Elaboración propia.

 

El 10.42% de los docentes poseen respuestas categorizadas en el nivel PE, es decir, son quienes responden incorrectamente o no distinguen ninguna dificultad para interpretar la representación de datos del ítem 20. Para ilustrar lo anterior, por ejemplo, P082 responde que “todas tienen la misma cantidad”, lo cual es relativo a cómo significa cada ícono en el cuerpo de datos de la tabla y la cantidad de estudiantes en el grupo encuestado. En el nivel UE se clasificaron el 45.83% de las respuestas de los docentes, lo que implicó que identificaran una sola dificultad posible vinculada a la interpretación de la tabla de datos. A modo de ejemplo, P021 responde que “no sale explicitado el valor de cada dibujo”, en otras palabras, reconoce la ausencia de la clave para cada ícono; además, P105 responde que una dificultad posible es “el tamaño de los dibujos, porque finalmente son la misma cantidad pero varía el tamaño”, destaca que falta la conservación de la unidad en un mismo tamaño para efectuar comparaciones; también P087 analiza, para el caso de la preferencia por la fruta guinda, que “(...) las puede contar por separado (8) o por conjunto (4)”, determinando que la frecuencia absoluta de dicha categoría de la variable puede interpretarse de dos formas: 8, o bien, 4 estudiantes prefieren la fruta guinda.

En el nivel ME, se clasificó el 35.42% de las respuestas, las cuales manifiestan dos o más dificultades que podría presentar un estudiante frente a la interpretación de la tabla de datos. En particular, por un lado, P065 responde que “las guindas las puede contar dobles. Podría agrupar por colores y confundir manzanas y guindas”, reconociendo que el conteo de los estudiantes que prefieren guinda puede producir un recuento de los racimos (frecuencia de 4 estudiantes), o bien, de las guindas (frecuencia de 8 estudiantes) como señaló el docente P087. Por otro lado, P191 responde que “el tamaño de cada fruta debería ser idéntico para todos. La distribución de espacio debería ser idéntica”, reconociendo no solo la conservación del tamaño del ícono en cada caso, sino también la conservación de los espacios entre íconos, ya que de esa manera puede evitarse una distorsión visual que impediría determinar la frecuencia correcta referida a la preferencia de frutas por un grupo de estudiantes.

En los niveles superiores R y A+, existen respuestas que argumentan un fundamento sobre las posibles dificultades identificadas. En el nivel R están clasificadas el 5.73% de las respuestas de los docentes; una respuesta en este nivel la construye P170 señalando que “cada guinda se considera como unidad o como dos unidades visualmente, también podría decir que hay menos cantidad por lo pequeño de la imagen. Por otro lado, un niño o niña podría decir que hay más plátanos por el tamaño, ya que visualmente se ve más”. Mientras en el nivel A+ solo está el 2.60% de las respuestas de los docentes; identificando más de dos dificultades fundamentadas, en particular, P094 responde que “en los plátanos y manzanas, visualmente, se destaca muy bien la cantidad; sin embargo, en las guindas podría confundirse entre cantidad de “racimos” y cantidad total de guindas. Podría decir: hay 4 guindas o hay 8 guindas. Otra dificultad es que podría considerar que prefieren más plátanos porque visualmente, la imagen de ellos es más larga en su extensión”, esto es, P094 pone de manifiesto cómo puede influir el diseño y tamaño del ícono en la frecuencia y, por ende, en la interpretación de los datos tabulados; además, P111 da una solución frente a ello, “(...) se podría colocar la imagen de la fruta [como categoría de la variable en el encabezado lateral] y con rayitas la cantidad de niños que las prefieren [tarjas de conteo en el cuerpo de datos].”, proponiendo así una nueva representación tabular, una tabla de conteo.

 

4.2. Análisis de las respuestas al ítem 21

 

Para la consigna: un objetivo de aprendizaje para 2° año básico es “construir, leer e interpretar pictogramas con escala y gráficos de barra simple”. Indique brevemente dos dificultades que podría tener algún estudiante para interpretar estadísticamente la siguiente representación de datos (ver Figura 2); las 192 respuestas al ítem 21 se clasificaron según la descripción propuesta, concordante a la taxonomía SOLO (ver Tabla 5).

 

Tabla 5

Distribución de las respuestas al ítem 21 relacionado a las posibles dificultades que pueden presentar estudiantes al interpretar una representación de datos, según taxonomía SOLO

Nivel SOLO	Frecuencia	Respuestas ilustrativas
PE	37 (19.27%)	P007. Cuántas se venden diariamente y quienes más la compran. P114. El color de la tabla tendría que ser más cerrada y los nombres de los meses más claros. P152. Resolver total de vueltas entre enero y junio. Cuál es la diferencia de vueltas dadas entre el mes con mayor y menor vueltas. P157. No considerar realizar un gráfico que le permita diferenciar y construir una respuesta en base a datos.
UE	101 (56.60%)	P034. No aplicar la escala. Confundirse al aplicar la escala. P083. (1) La imagen cortada confunde a los estudiantes; (2) Tiene dos escalas (100, 50). P094. Podría considerar que las bicicletas dibujadas bajo junio corresponden al mes de Julio. P101. Discernir sobre la cantidad de venta de bicicletas. P132. Poner la mitad de la bicicleta podría inducir a que se relaciones a falla del dibujo en sí. La escala utilizada debe estar sujeta a solo un valor numérico. P133. Dibujos mal seleccionados, ya que los niños tienden a fijarse en el dibujo más que en el valor otorgado a cada uno. P136. Hábito numérico de 2° año básico. Concepto de fracción o parte de un elemento. P163. Inexistentes las medias bicicletas. P189. Creo que les complicaría las mitades de bicicletas.
ME	46 (23.96%)	P072. Darle valor 1 en vez de 100 y no contabilizar una media bicicleta. P116. Problemas con el conteo y con comprender el valor de la mitad de la bicicleta. P143. Pasar de largo las claves de valor y contar las bicicletas como si fueran una sola. P149. (1) Que no tome en cuenta los valores de cada indicador (100, 50); (2) Calcular el total de ventas de bicicletas del semestre. P151. Saber que 50 es la mitad los confunde bastante al contar porque aún no ven fracciones y concretamente no es lo mismo media bicicleta que una entera.
R	8 (4.17%)	P020. Podría no darse cuenta del valor que representa una bicicleta o media, y simplemente contar 2 en lugar de 200. Un problema adicional es comprender qué valor tiene media bicicleta. P045. (1) Que no sepa relacionar la mitad de la bicicleta como 50 bicicletas vendidas; (2) Que cuente las bicicletas vendidas en cada mes por unidad. Ejemplo: en marzo se vendieron 3 bicicletas y no 300. P089. No entender la mitad de la bicicleta y no saber sumar una bicicleta más media bicicleta. P174. (1) No considerar la leyenda del gráfico donde se indica el valor que representa una bicicleta y la mitad de una bicicleta; (2) Contar solo las bicicletas que están completas.

Nota. Las respuestas seleccionadas para cada nivel de la taxonomía SOLO son ilustrativas, no pretenden ser representativas del nivel. Elaboración propia.

 

En el nivel PE se clasificó el 19.27% de las respuestas de los docentes, quienes no logran identificar dificultad alguna, o bien, responden de forma incorrecta. Para ilustrar lo anterior, por ejemplo, P152 responde como posible dificultad que el “resolver [el] total de vueltas entre enero y junio. Cuál es la diferencia de vueltas dadas entre el mes con mayor y menor vueltas”, esto evidencia que no logró reconocer la variable estadística en juego –i.e., ventas de bicicletas en el 1° semestre– que presenta el ítem 21. Mientras que, en el nivel UE, se clasificaron el 56.60% de las respuestas de los docentes, quienes identifican una posible dificultad frente a la interpretación de la tabla de datos que podría tener cierto estudiante. En particular, P133 responde que los “dibujos [están] mal seleccionados, ya que los niños tienden a fijarse en el dibujo más que en el valor otorgado a cada uno”, es decir, P133 critica la selección del ícono bicicleta y su mitad, al igual que P163, pues responde que es “inexistente las medias bicicletas” de acuerdo con el contexto que portan los datos. Por su parte, P034 responde que: “no aplicar la escala [clave]. Confundirse al aplicar la escala [clave]”, manifestando que posee una confusión entre el concepto de escala y clave, ya que la clave es la que relaciona la cantidad de datos que representa el ícono, en este caso, el ícono bicicleta completo representa la venta de 100 bicicletas, mientras que la mitad del ícono bicicleta equivale a la venta de 50 bicicletas. Esta última idea, coincide con la respuesta de P083 porque argumenta que: “(1) La imagen cortada confunde a los estudiantes; (2) Tiene dos escalas [claves] (100, 50)”, de igual manera, P132 responde que “poner la mitad de la bicicleta podría inducir a que se relacione a falla del dibujo en sí. La escala [clave] utilizada debe estar sujeta a solo un valor numérico”.

En el nivel ME se clasificaron el 23,96% de las respuestas de los docentes, quienes identifican dos o más dificultades frente a la interpretación tabular del ítem 21. En particular, P143 responde que “pasar de largo [omitir] las claves de valor y contar las bicicletas como si fueran una sola”; también P072 agrega que “darle valor 1 en vez de 100 y no contabilizar una media bicicleta”, manifiestan un problema posible para la determinación de la frecuencia absoluta relacionada con las ventas de bicicletas en cada uno de los meses del 1° semestre.

En los niveles superiores, solo se tienen respuestas de docentes en el nivel R y no así en el nivel A+, en estos niveles existe un fundamento sobre las dificultades identificadas. En el nivel R están clasificadas el 4.17% de las respuestas de los docentes, por ejemplo, P045 responde que “(1) Que [el estudiante] no sepa relacionar la mitad de la bicicleta como 50 bicicletas vendidas; (2) Que cuente las bicicletas vendidas en cada mes por unidad. Ejemplo: en marzo se vendieron 3 bicicletas y no 300”; asimismo, P089 posee una respuesta más específica: “no entender la mitad de la bicicleta y no saber sumar una bicicleta más media bicicleta”, lo cual puede estar vinculado al contexto de los datos en tanto no existe la mitad de una bicicleta en el mundo real y su interpretación puede volverse complejo para un estudiante en los primeros niveles de enseñanza estadística, dado que requiere un nivel de abstracción mayor para relacionar proporcionalmente una cantidad y su mitad.

 

4.3. Evidencias del KFSL

 

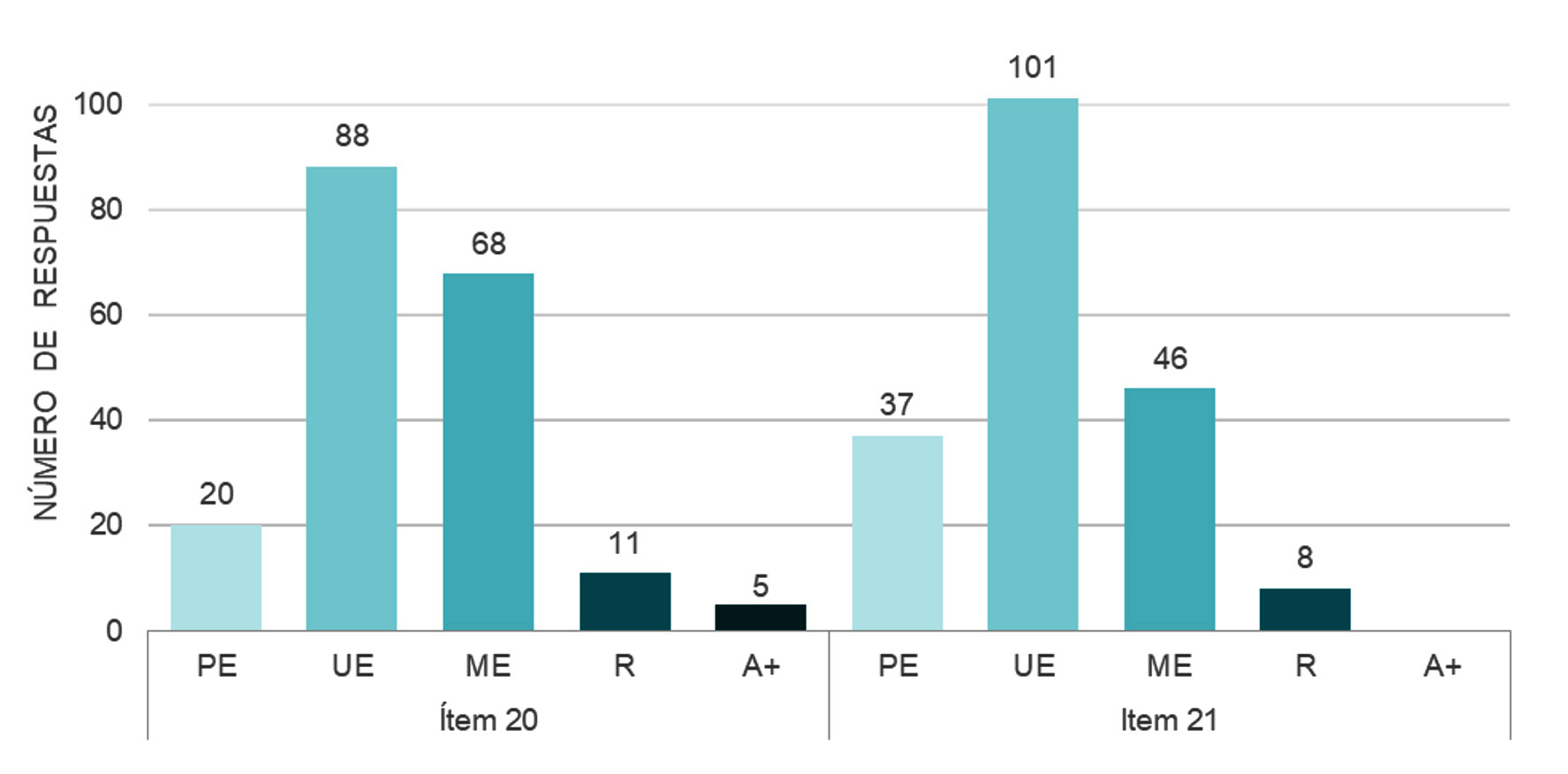
La figura 3 da cuenta del comportamiento de las respuestas clasificadas, según la taxonomía SOLO a modo de síntesis del análisis anterior.

 

Figura 3

Distribución de respuestas a los ítems 20 y 21, según los niveles de la taxonomía SOLO

 

A continuación, se exhiben ciertas evidencias de la manifestación del KFSL en profesores de estadística que enseñan en educación básica, tomando en cuenta la clasificación de las respuestas a los ítems 20 y 21 en los niveles ME, R y A+.

(A) Fortalezas y debilidades en el aprendizaje de la estadística. En el ítem 20, P170 analiza una posible dificultad, respondiendo que como “(...) hay más plátanos por el tamaño, (…) visualmente se ve más”, es decir, identifica que la tabla de datos representados por íconos en dicho ítem produciría dificultades para determinar la frecuencia mayor. En el ítem 21, P136 responde que el ámbito numérico que habitualmente posee un estudiante de 2° año básico, puede impedir la correcta interpretación del ícono de bicicleta a su mitad como clave en la representación de datos en dicho ítem, porque ello demanda tener conocimiento de la noción de fracción como “parte de un elemento” (parte-todo). Estos docentes dan evidencias de un KFSL en la categoría (A) Fortalezas y debilidades en el aprendizaje de la estadística, pues están movilizando y anticipando en sus respuestas posibles dificultades que pueden expresar los estudiantes en sus producciones al interpretar las representaciones de datos que poseen los ítems 20 y 21.

(B) Tipos de interacción de los estudiantes con el contenido estadístico. En el ítem 20, P065 señala que, tomando en consideración el procedimiento de los estudiantes en 1° año básico para calcular la frecuencia absoluta en la representación de datos, “las guindas las puede contar dobles”, y agrega que algún estudiante “podría agrupar por colores y confundir manzanas y guindas”. En el ítem 21, P045 indica que un estudiante de 2° año básico puede efectuar el siguiente procedimiento “que cuente las bicicletas vendidas en cada mes por unidad”, inclusive anticipa lo que ocurriría como conclusión incorrecta “(...) en marzo se vendieron 3 bicicletas y no 300”, obviando la clave de la representación de datos. Estos docentes dan evidencias de un KFSL en la categoría (B) Tipos de interacción de los estudiantes con el contenido estadístico, porque involucran en sus respuestas impedimentos posibles que los estudiantes pueden manifestar al calcular la frecuencia absoluta dadas las estrategias de conteo que pueden emplear como procedimiento.

 

5. CONCLUSIONES

 

Esta investigación buscó ampliar la comprensión sobre la extensión del modelo MTSK —Conocimiento Especializado del Profesor de Matemáticas— a la disciplina Estadística, nombrado modelo STSK (i. e., Statistics Teacher´s Specialized Knowledge). En ese sentido, el propósito fue caracterizar los conocimientos y niveles de comprensión que expresan profesores que enseñan estadística en educación básica, referido a las características del aprendizaje de la estadística de los estudiantes. A partir del análisis de las 384 respuestas de docentes, se obtuvo que solo un 36% de dichas respuestas están en los niveles superiores de la taxonomía SOLO (Multiestructural, Relacional y Abstracto ampliado; respuestas totalmente correctas al ítem), las cuales manifiestan un conocimiento especializado del profesor de estadística en el subdominio KFSL, conocimiento de las características del aprendizaje estadístico en las categorías (a) fortalezas y debilidades en el aprendizaje de la estadística y (b) tipos de interacción de los estudiantes con el contenido estadístico.

Los ejemplos examinados y previamente clasificados, respaldan la manifestación del KFSL, pues constituye un conjunto de conocimientos en dicho subdominio que pueden ser movilizados por profesores en su actuar profesional en el área de la educación estadística. En virtud de dicha clasificación, realizada para determinar evidencias de KFSL, es posible que los resultados de este estudio puedan contribuir como referencia para la formación de profesores que enseñan estadística en los primeros años escolares, porque brinda acceso a la profundización de conocimientos especializados relacionado con el dominio PCK. Tal como lo muestran los resultados, se sugiere potenciar en la formación inicial y continua de profesores, el conocimiento especializado referido al subdominio KFSL (en sus categorías a y b), pues el 64% aproximadamente de las respuestas se clasificaron en los niveles más bajos de la taxonomía SOLO.

El presente estudio aporta al conocimiento teórico especializado vinculado con la formación docente en estadística temprana, al caracterizar cierto conocimiento didáctico del contenido del profesorado, mediante categorías y descripciones propuestas y evidenciadas del subdominio conocimiento de las características del aprendizaje de la estadística del modelo STSK, no exhaustivas todavía. En consecuencia, se proyecta continuar investigando en el área de la Estadística Temprana, en particular, en los dominios de conocimiento del modelo STSK, profundizando en los subdominios del conocimiento didáctico del contenido y su relación con el conocimiento estadístico, pues el modelo STSK sigue en desarrollo y ha resultado de interés para la comunidad de educadores estadísticos, en tanto permite precisar los conocimientos especializados del profesorado que enseña estadística en distintos niveles educativos.

 

Agradecimientos

Esta investigación ha sido financiada parcialmente por ANID a través de CONICYT-PCHA/Doctorado Nacional: 2016-21161569. También ha sido patrocinada por el Grupo de Investigación en Estadística Temprana (GIET, https://estadisticatemprana.cl/).

 

REFERENCIAS BIBLIOGRÁFICAS

 

Agencia de Calidad de la Educación (2016). Estudio Preguntas Abiertas Matemática TIMSS 2015: ¿Qué podemos aprender de las equivocaciones de estudiantes de 8° básico en matemática? ACE. http://archivos.agenciaeducacion.cl/WEB_TIMSS_MATEMATICAS_8_2015.pdf

Australian Curriculum, Assessment and Reporting Authority. (2013). The Australian curriculum. Author. https://www.australiancurriculum.edu.au/about-theaustralian-curriculum/

Ball, D.L., Thames, M.H. y Phelps, G. (2008). Content knowledge for teaching: What makes it special? Journal of Teacher Education, 59(5), 389-407. https://doi.org/10.1177/0022487108324554

Ben-Zvi, D. y Garfield, J. (2004). Statistical literacy, reasoning, and thinking: goals, definitions, and challenges. En D. Ben-Zvi y J. Garfield (Eds.), The challenge of developing statistical literacy, reasoning, and thinking (pp. 3-15). Kluwer Academic Publishers, Springer. https://philarchive.org/archive/CAPTEO

Biggs, J. y Collis, K. F. (1989). Towards a Model of School-based Curriculum Development and Assessment Using the SOLO Taxonomy. Australian Journal of Education, 33, 151-163. https://doi.org/10.1177/168781408903300205

Carrillo, J., Climent, N., Contreras, L.C. y Muñoz-Catalán, M.C. (2013). Determining specialised knowledge for mathematics teaching. En B. Ubuz, Ç. Haser y M.A. Mariotti (Eds.), Proceedings of the Eighth Congress of the European Society for Research in Mathematics Education (pp. 2985-2994). Middle East Technical University. http://www.mathematik.uni-dortmund.de/~erme/doc/CERME8/CERME8_2013_Proceedings.pdf#page2985

Carrillo, J., Climent, N., Montes, M., Contreras, L., Flores-Medrano, E., Escudero-Ávila, D., Vasco, D., Rojas, N., Flores, P., Aguilar-González, A., Ribeiro, M. y Muñoz-Catalán, M.C. (2018). The mathematics teacher’s specialized knowledge (MTSK) model. Research in Mathematics Education, 20(3), 1-18. https://doi.org/10.1080/14794802.2018.1479981

Chick, H. (1998). Cognition in the formal modes: Research mathematics and the SOLO taxonomy. Math Ed Res J, 10, 4-26. https://doi.org/10.1007/BF03217340

Cobb, G. W. y Moore, D.S. (1997). Mathematics, statistics, and teaching. The American Mathematical Monthly, 104(9), 801-823. https://doi.org/10.1080/00029890.1997.11990723

Codes, M., Moriel-Junior, J., Alfaro, C. y González, Y. (2020). Síntesis y problemas abiertos en el IV Congreso iberoamericano de conocimiento especializado del profesor de matemáticas (MTSK). En J. Carrillo, M. Codes y L.C. Contreras (Eds.), IV Congreso Iberoamericano sobre Conocimiento Especializado del Profesor de Matemáticas (pp. 41-47). Universidad de Huelva. https://cdn.congresse.me/rlbmixa8vqmkkc75l9pjf2p8ex1i

Common Core State Standards Initiative. (2017). Mathematics standards. http://www.corestandards.org/Math/

Del Pino, G. y Estrella, S. (2012). Educación Estadística: relaciones con la matemática. Pensamiento Educativo, Revista de Investigación Educacional Latinoamericana, 49(1), 53-64.

English, L. (2010). Young children’s early modelling with data. Mathematics Education Research Journal, 22, 24-47. https://doi.org/10.1007/BF03217564

English, L. (2012). Data modeling with first-grade students. Educational Studies in Mathematics, 81(1), 15-30. https://doi.org/10.1007/s10649-011-9377-3

English, L. (2018). Young children’s statistical literacy in modelling with data and chance. En A. Leavy, M. Meletiou-Mavrotheris y E. Paparistodemou, Statistics in Early Childhood and Primary Education. Early Mathematics Learning and Development (pp. 295-313). Springer. https://doi.org/10.1007/978-981-13-1044-7_17

Escobar, J. y Cuervo, A. (2008). Validez de contenido y juicio de expertos: una aproximación a su utilización. Avances en Medición, 6, 27-36.

Estrella, S. (2017). Enseñar estadística para alfabetizar estadísticamente y desarrollar el razonamiento estadístico. En A. Salcedo (Ed.), Alternativas Pedagógicas para la Educación Matemática del Siglo XXI (pp. 173-194). Centro de Investigaciones Educativas, Escuela de Educación. Universidad Central de Venezuela.

Estrella, S. (2018). Data representations in Early Statistics: data sense, meta-representational competence and transnumeration. En A. Leavy, M. Meletiou y E. Paparistodemou (Eds.), Statistics in Early Childhood and Primary Education – Supporting early statistical and probabilistic thinking (pp. 239-256). Springer. https://doi.org/10.1007/978-981-13-1044-7_14

Estrella, S., Alvarado, H., Olfos, R. y Retamal, L. (2019). Desarrollo de la alfabetización probabilística: textos argumentativos de estudiantes (según niveles de razonamiento de la taxonomía SOLO). Revista Paradigma, 40(1), 280-304.

Estrella, S., Méndez-Reina, M. y Vidal-Szabó, P. (2023). Exploring informal statistical inference in early statistics: a learning trajectory for third-grade students. Statistics Education Research Journal. (on going).

Estrella, S., Olfos, R., Vidal-Szabó, P., Morales, S. y Estrella, P. (2018). Competencia metarrepresentacional en los primeros grados: representaciones externas de datos y sus componentes. Revista Enseñanza de las Ciencias, 36(2), 143-163. https://ensciencias.uab.es/article/view/v36-n2-estrella-olfos-vidal-etal

Estrella, S., y Vidal-Szabó, P. (2017). Alfabetización estadística a través del Estudio de Clase: representaciones de datos en primaria. Uno, Revista de Didáctica de las Matemáticas, 78, 12-17. https://www.researchgate.net/publication/352118213_Alfabetizacion_estadistica_a_traves_del_Estudio_de_Clase_representaciones_de_datos_en_primaria#fullTextFileContent

Estrella, S., Vidal-Szabó, P. y Morales, S. (2022). Enseñanza de la estadística en Chile con Lesson Study: innovaciones y buenas prácticas. En A. Salcedo y D. Díaz-Levicoy (Eds.), Formación del Profesorado para Enseñar Estadística: Retos y Oportunidades (pp. 137-163). Centro de Investigación en Educación Matemática y Estadística, Universidad Católica del Maule.

Flores, E., Escudero, D.I. y Carrillo, J. (2013). A theoretical review of specialized content knowledge. En B. Ubuz, C. Haser y M.A. Mariotti (Eds.), Proceedings of CERME8 (pp. 3055-3064). Middle East Technical University.

Garfield, J. y Ben-Zvi, D. (2008). Developing students’ statistical reasoning: Connecting research and teaching practice. Springer Science y Business Media. https://doi.org/10.1007/978-1-4020-8383-9

Groth, R. (2007). Toward a conceptualization of statistical knowledge for teaching. Journal for Research in Mathematics Education, 38, 427-437. https://www.jstor.org/stable/30034960

Groth, R. (2017). Developing statistical knowledge for teaching during design-based research. Statistics Education Research Journal, 16(2), 376-396.

Groth, R. y Bergner, J. (2013). Mapping the structure of knowledge for teaching nominal categorical data analysis. Educ Stud Math, 83, 247-265. https://doi.org/10.1007/s10649-012-9452-4

Ministerio de Educación de Chile. (2012). Bases Curriculares para la Educación Básica. http://www.curriculumenlineamineduc.cl/605/articles-21321_programa.pdf

Moore, D. (1997). New pedagogy and new content: The case of statistics. International Statistical Review, 65(2), 123-165. https://iase-web.org/documents/intstatreview/97.Moore.pdf

New Zealand Ministry of Education. (2007). The New Zealand curriculum. Learning Media. https://nzcurriculum.tki.org.nz/The-New-Zealand-Curriculum

Pfannkuch, M. (2011). The role of context in developing informal statistical inferential reasoning: A classroom study. Mathematical Thinking and Learning, 13(1 y 2), 27-46. https://doi.org/10.1080/10986065.2011.538302

Pfannkuch, M. y Wild, C. (2000). Statistical thinking and statistical practice: Themes gleaned from professional statisticians. Statistical Science, 15(2), 132-152. https://doi.org/10.1214/ss/1009212754

Scheiner, T., Montes, M.A., Godino, J.D., Carrillo, J. y Pino-Fan, L.R. (2019). What makes mathematics teacher knowledge specialized? Offering alternative views. International Journal of Science and Mathematics Education, 17(1), 153-172. https://doi.org/10.1007/s10763-017-9859-6

Seguí, J.F. y Alsina, A. (2022). Conocimiento especializado del profesorado de Educación Primaria para enseñar estadística y probabilidad. Revista Educación Matemática, 34(3), 65-96. https://doi.org/10.24844/EM3403.03

Vidal-Szabó, P. (2021). Enseñar y Aprender Estadística desde los Primeros Años de Escolaridad. En A. Pizarro, C. Caamaño y M. C. Brieba (Eds.), Didáctica de la Matemática para Primer Ciclo de Educación Básica: Aportes a la Formación Continua de Profesores, Tomo I (pp. 130-155). Ediciones Universitarias de Valparaíso.

Vidal-Szabó, P. y Estrella, S. (2020). Extensión del modelo MTSK al dominio estadístico. En Y. Morales-López y Á. Ruíz (Eds.), Educación Matemática en las Américas 2019 (pp. 1036-1042). Comité Interamericano de Educación Matemática.

Vidal-Szabó, P. y Estrella, S. (2021). Conocimiento Estadístico Especializado en Profesores de Educación Básica, basado en la taxonomía SOLO. Revista Chilena de Educación Matemática, 13(4), 134-148. https://doi.org/10.46219/rechiem.v13i4.81

Vidal-Szabó, P., Kuzniak, A., Estrella, S. y Montoya, E. (2020). Análisis cualitativo de un aprendizaje estadístico temprano con la mirada de los espacios de trabajo matemático orientado por el ciclo investigativo. Revista Educación Matemática, 32(2), 217-246. https://doi.org/10.24844/EM3202.09

Wild, C. y Pfannkuch, M. (1999). Statistical thinking in empirical enquiry. International Statistical Review, 67(3), 223-265. https://doi.org/10.1111/j.1751-5823.1999.tb00442.x

Wild, C., Utts, J. y Horton, N. (2018). What is statistics? En D. Ben-Zvi, K. Makar y J. Garfield (Eds.), International Handbook of Research in Statistics Education (pp. 5-36). Springer. https://doi.org/10.1007/978-3-319-66195-7_2

Zieffler, A., Garfield, J. y Fry, E. (2018). What is Statistics Education? En D. Ben-Zvi, K. Makar y J. Garfield (Eds.), International Handbook of Research in Statistics Education (pp. 37-70). Springer. https://doi.org/10.1007/978-3-319-66195-7_2

 

Como citar:

Vidal-Szabó, P. y Estrella, S. (2023). Explorando la extensión del modelo MTSK al dominio estadístico: características del aprendizaje desde la Taxonomía SOLO. Revista de Educación Estadística, 2(1), 1-25. https://doi.org/10.29035/redes.2.1.3

 

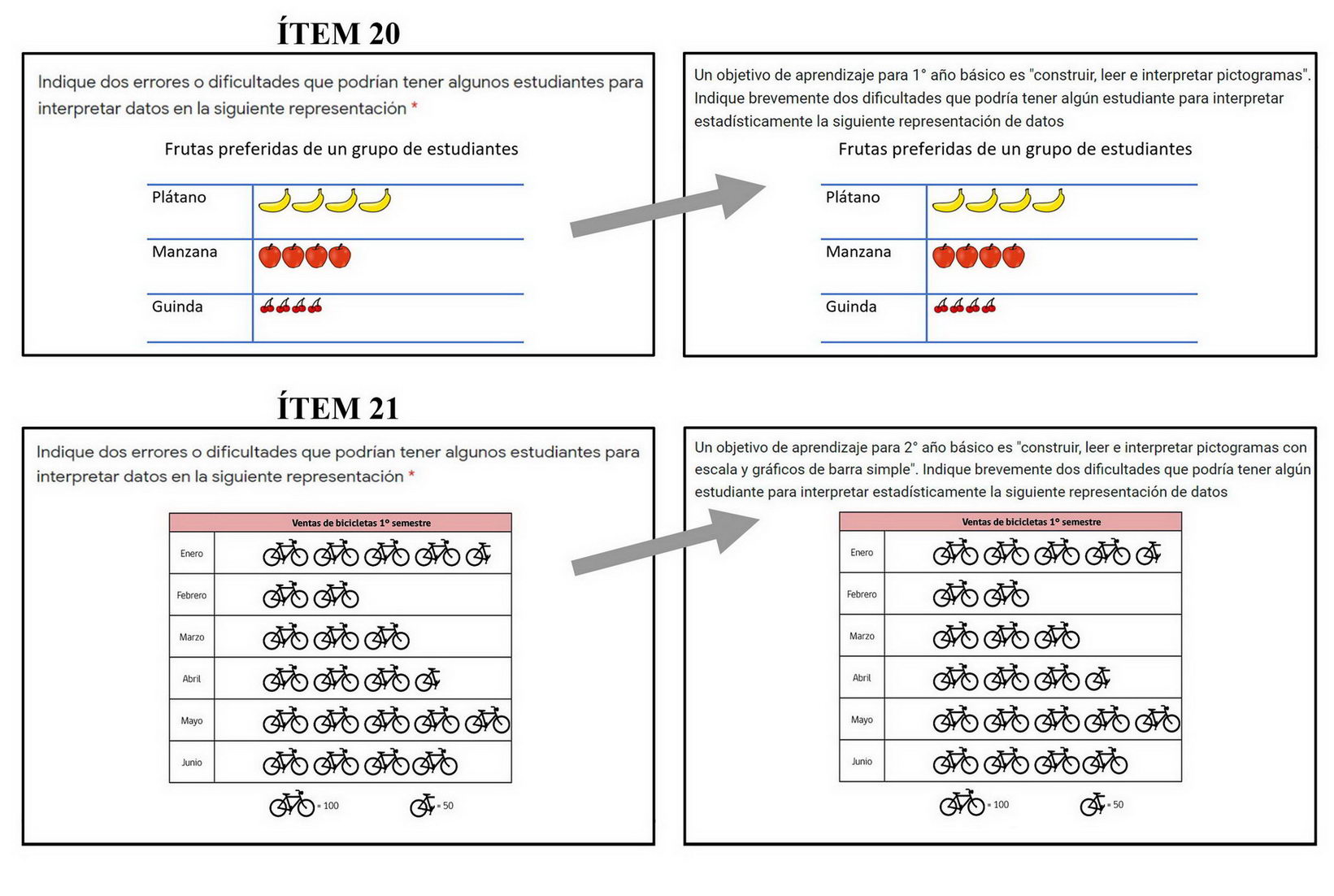
Anexo 1.

Reformulación de las consignas de los ítems 20 y 21

 

Esta obra está bajo una licencia de Creative Commons
Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional.