Revista de Educación Estadística https://revistaeduest.ucm.cl/ Vol. 2, n. 1, 1-25, abr. 2023 - sep. 2023 ISSN 2810-6164

DOI: https://doi.org/10.29035/redes.2.1.1

PROBABILIDADE EM AÇÃO: APRESENTANDO UM JOGO DE TABULEIRO PARA O ENSINO DE PROBABILIDADE NOS ANOS INICIAIS

Probabilidad en acción: Presentamos un juego de mesa para enseñar la probabilidad en los primeros años

Probability in action: Presenting a board game to teach probability in the early years

Ailton Paulo de Oliveira Júnior*1

Universidade Federal do ABC (Santo André/SP, Brasil)

Nilceia Datori Barbosa2

Universidade Federal do ABC (Santo André/SP, Brasil)

 

Resumo

O objetivo deste trabalho foi apresentar um jogo de tabuleiro para auxiliar alunos e professores nos processos de ensino e aprendizagem da probabilidade. O jogo é voltado para os anos iniciais do Ensino Fundamental e contém todos os objetos de conhecimento e habilidades propostos pela Base Nacional Comum Curricular – BNCC, dentre outros importantes documentos que norteiam o ensino de probabilidade. O jogo é composto por um percurso e dois tipos de cartas: (1) Perguntas: que são situações problemas envolvendo conteúdos de probabilidade; (2) Saiba mais: que trazem informações probabilísticas. Para o desenvolvimento do jogo nós nos apoiamos na metodologia de design iterativo proposta por Eric Zimmerman que é baseada num processo cíclico de prototipagem, teste, análise e refinamento. O jogo apresenta diversos elementos da aleatoriedade em sua estrutura e, portanto, consideramos que além de aproximar as crianças da probabilidade também tem potencial de proporcionar reflexões importantes sobre os conceitos probabilísticos em maior ou menor grau, dependendo da mediação do professor. Esse trabalho vislumbra a contribuição dos jogos como ferramenta auxiliar para o ensino de probabilidade visto que, quando inseridos no contexto escolar, podem potencializar o desenvolvimento de habilidades e auxiliar no processo de aprendizagem de conceitos.

Palavras-chave: Jogo pedagógico, Ensino de probabilidade, Anos iniciais do Ensino Fundamental, Design iterativo.

 

Resumen

El objetivo de este trabajo fue presentar un juego de mesa para ayudar, a estudiantes y docentes, en los procesos de enseñanza y aprendizaje de la probabilidad. El juego está dirigido a los primeros años de la escuela primaria y contiene todos los objetos de conocimiento y habilidades propuestos por la Base Nacional Común Curricular - BNCC, entre otros documentos importantes que orientan la enseñanza de la probabilidad. El juego consta de un curso y dos tipos de tarjetas: (1) Preguntas: que son situaciones problema que involucran contenido de probabilidad; (2) Saber más: que aportan información probabilística. Para el desarrollo del juego, nos basamos en la metodología de diseño iterativo propuesta por Eric Zimmerman, la cual se basa en un proceso cíclico de prototipado, prueba, análisis y refinamiento. El juego tiene varios elementos de aleatoriedad en su estructura y, por ello, creemos que además de acercar a los niños a la probabilidad, también tiene el potencial de aportar importantes reflexiones sobre conceptos probabilísticos en mayor o menor medida, dependiendo de la mediación del profesor. Este trabajo contempla el aporte de los juegos como una herramienta auxiliar para la enseñanza de la probabilidad ya que, al insertarse en el contexto escolar, puede potenciar el desarrollo de habilidades y ayudar en el proceso de aprendizaje de conceptos.

Palabras clave: Juego pedagógico, Enseñanza de la probabilidad, Primeros años de primaria, Diseño iterativo.

 

Abstract

The objective of this work was to present a board game to help students and teachers in the teaching and learning processes of probability. The game is aimed at the early years of elementary school and contains all the objects of knowledge and skills proposed by the National Common Curricular Base - BNCC, among other important documents that guide the teaching of probability. The game consists of a course and two types of cards: (1) Questions: which are problem situations involving probability contents; (2) Learn more: that bring probabilistic information. For the development of the game, we relied on the iterative design methodology proposed by Eric Zimmerman which is based on a cyclic process of prototyping, testing, analysis and refinement. The game has several elements of randomness in its structure and, therefore, we believe that in addition to bringing children closer to probability, it also has the potential to provide important reflections on probabilistic concepts to a greater or lesser extent, depending on the teacher’s mediation. This work envisages the contribution of games as an auxiliary tool for teaching probability, since when inserted in the school context they can enhance the development of skills and help in the process of learning concepts.

Keywords: Pedagogical game, Probability teaching, Early years of elementary school, Iterative design.

 

Recibido: 30/01/2023 - Aceptado: 10/04/2023

 

1. INTRODUÇÃO

 

Partindo do nosso objeto de estudo e a realização de uma Revisão Sistemática de Literatura – RSL (Oliveira Júnior e Datori Barbosa, 2023, submetido à publicação) revelou-se a importância da utilização de jogos pedagógicos como ferramenta para o ensino e aprendizagem da probabilidade, devido ao seu caráter lúdico e desafiador, que permite ao professor conhecer o perfil do aluno e interagir com seu pensamento probabilístico. Além disso, identificou-se uma lacuna a ser preenchida em relação à criação, desenvolvimento e utilização de jogos de tabuleiro e digitais para o ensino de probabilidade para alunos de 6 a 10 anos, na qual, buscou-se com esse trabalho, dar continuidade à pesquisa desenvolvida por Datori Barbosa (2019) ampliando o jogo pedagógico “Brincando com a Probabilidade”.

Assim, nesse texto, trata-se de um jogo de tabuleiro, tipo percurso, com problemas convencionais que depende da sorte e de respostas assertivas. O tabuleiro estrutura um espaço e relações entre objetos neste espaço, tornando possível uma experiência lúdica e agradável, que gera prazer funcional (Instituto Avisa Lá, 2021).

Sobre a ludicidade, de acordo com Silva e Souza (2021) os jogos podem ser considerados como atividades potencialmente lúdicas, isto é, atividades pensadas e planejadas pelo professor com o propósito de oferecer prazer em sua realização. É importante esclarecer e frisar que a ludicidade não se restringe a jogos e brincadeiras, mas sim a toda atividade planejada pelo professor com o intuito de promover prazer ao realizá-la.

Para Luckesi (2014), a ludicidade pode ser considerada como um estado interno do sujeito, em que o que é prazeroso para um indivíduo pode não ser prazeroso para outro. A este respeito, Grando et al. (2022) reforçam que o lúdico requer envolvimento, atitude, vontade de fazer e estar, ou seja, é algo subjetivo. Ainda, por ser considerado um afeto (desafiador) o lúdico incita a pessoa a querer permanecer envolvido num comportamento lúdico, contudo, isso ocorre somente enquanto o indivíduo estiver se sentindo desafiado e/ou atribuindo sentido no ato de jogar.

Destacamos que o jogo apresentado neste trabalho conta com 89 situações problemas ou desafios (cartas “Pergunta”) para serem resolvidos. Além dessas cartas, o jogo também é composto por 24 cartas tipo “Saiba Mais”, que trazem curiosidades/informações probabilísticas de diversas áreas do conhecimento.

Nessa perspectiva lúdica, o jogo traz a resolução de problemas nas questões contidas nas cartas tipo “Pergunta” de forma que, a partir do jogo, o aluno resolverá diversos problemas envolvendo conceitos probabilísticos para avançar no tabuleiro e vencer a partida. É importante frisar que, embora os problemas sejam convencionais, eles possibilitam a experimentação em sala de aula e ainda, por se tratar de um jogo, abre possibilidades de aproveitamento do aspecto lúdico para trabalhar com os conceitos de probabilidade.

As situações problemas contidas nas cartas do jogo abordam todos os objetos de conhecimento probabilísticos para os anos iniciais do Ensino Fundamental segundo a Base Nacional Comum Curricular – BNCC (Ministério da Educação, 2018) de maneira conectada com o programa de ensino desenvolvido por Bryant e Nunes (2012) publicado pela Fundação Nuffield da Universidade de Oxford.

Na continuidade do trabalho, buscou-se ampliar os aspectos pedagógicos do jogo, incluindo o documento norte-americano Diretrizes para Avaliação e Instrução em Ensino de Estatística - GAISE II em Bargagliotti et al. (2020) por incorporar o pensamento probabilístico na quantificação da aleatoriedade para o ensino de estatística em todos os níveis de ensino da Educação Básica.

Com base nesses constructos, o jogo foi reestruturado para oferecer ao professor possibilidades de trabalho em sala de aula, baseadas na verbalização, visando subsídios para o desenvolvimento das noções probabilísticas. Essas possibilidades incluem utilizar o jogo tanto para avaliar os conhecimentos prévios das crianças, como para introduzir um assunto que depois poderá ser desenvolvido com mais tempo em sala de aula, ou, introduzir um assunto em sala de aula e depois reforçar com o jogo, como também para aprofundar um objeto de conhecimento em específico.

Essa ampliação trouxe também a possibilidade ao professor de criar novas cartas para compor o jogo, bem como a realização de alguns experimentos em sala de aula que estiverem propostos nestas cartas, promovendo assim, oportunidade de intervenção em prol da construção dos conceitos probabilísticos.

Desta forma, envolvendo a probabilidade num ambiente lúdico de um jogo de tabuleiro, pretendemos propiciar a sensação de se estar em oposição a uma situação formal de aprendizado, oportunizando espaço para que as falas, trocas de ideias e argumentações discorram de forma mais natural e espontânea possível.

 

2. APRESENTANDO A BNCC, O PROGRAMA DE ENSINO DA FUNDAÇÃO NUFFIELD E O DOCUMENTO GAISE II PARA O ENSINO DE PROBABILIDADE PARA OS ANOS INICIAIS DO ENSINO FUNDAMENTAL

 

O jogo contém todos os objetos de conhecimento e habilidades apontados pela BNCC (Ministério da Educação, 2018), que em sua proposta incorporou a probabilidade em uma das unidades temáticas a serem trabalhadas nos anos iniciais, a unidade denominada Probabilidade e Estatística. De acordo com a BNCC, o estudo das probabilidades nos anos iniciais do Ensino Fundamental tem a finalidade de promover a compreensão de que nem todos os eventos são determinísticos. Sendo assim, o trabalho inicial com probabilidade deve focar o desenvolvimento da noção de aleatoriedade, de forma que os alunos compreendam que existem eventos certos, eventos impossíveis e eventos possíveis.

De forma gradativa, dentre os eventos aleatórios possíveis, iniciam-se as análises entre os eventos, tais como: pouco provável, muito provável, improvável, igualmente provável e equiprovável. Parte-se da ideia de que é muito comum que pessoas julguem impossíveis eventos que nunca viram acontecer. Assim, nessa fase, é importante que os alunos verbalizem, em eventos que envolvem o acaso, os resultados que poderiam ter acontecido em oposição ao que realmente aconteceu, iniciando a construção do espaço amostral e a apropriação de um repertório linguístico probabilístico.

Os objetos de conhecimento probabilísticos a serem abordados, de acordo com a BNCC (Ministério da Educação, 2018), para os anos iniciais do Ensino Fundamental (6 a 10 anos), são apresentados no Tabela 1 (Descrição dos objetos de conhecimento e descrição das habilidades).

 

Tabela 1

Objetos e Habilidades de Probabilidade propostos na BNCC do 1° ao 5° ano do Ensino Fundamental (6 a 10 anos)

	1° ano	2° ano	3° ano	4° ano	5° ano
Objetos	Noção de acaso.	Análise da ideia de aleatório em situações do cotidiano.	Análise da ideia de acaso em situações do cotidiano: espaço amostral.	Análise de chances de eventos aleatórios.	Espaço amostral: análise de chances de eventos aleatórios.	Cálculo de probabilidade de eventos equiprováveis.
Habilidades	EF01MA20 Classificar eventos envolvendo o acaso, tais como “acontecerá com certeza”, “talvez aconteça” e “é impossível acontecer”, em situações do cotidiano.	EF02MA21 Classificar resultados de eventos cotidianos aleatórios como “pouco prováveis”, “muito prováveis”, “improváveis” e “impossíveis”.	EF03MA25 Identificar, em eventos familiares aleatórios, todos os resultados possíveis, estimando os que têm maiores ou menores chances de ocorrência.	EF04MA26 Identificar, entre eventos aleatórios cotidianos, aqueles que têm maior chance de ocorrência, reconhecendo características de resultados mais prováveis, sem utilizar frações.	EF05MA22 Apresentar todos os possíveis resultados de um experimento aleatório, estimando se esses resultados são igualmente prováveis ou não.	EF05MA23 Determinar a probabilidade de ocorrência de um resultado em eventos aleatórios, quando todos os resultados possíveis têm a mesma chance de ocorrer, equiprováveis.

Fonte: Ministério da Educação (2018, p. 280-281; 284-285; 288-289; 292-293; 296-297)

 

Godino et al. (1996), destacam que a probabilidade pode ser aplicada à realidade tão diretamente quanto à aritmética elementar, pois não é preciso lançar mão de teorias físicas e nem técnicas matemáticas complicadas.

É neste contexto que a probabilidade proporciona uma excelente oportunidade para mostrar aos alunos como matematizar, como aplicar a matemática para resolver problemas reais (Godino et al., 1996). Para que isso ocorra é preciso que o ensino das noções probabilísticas aconteça mediante uma metodologia heurística e ativa, através de propostas de problemas concretos e da realização de experimentos reais ou simulada.

A aprendizagem da probabilidade contribui para o desenvolvimento do pensamento crítico, que permite aos cidadãos compreender e comunicar diferentes tipos de informação presentes em inúmeras situações da vida cotidiana nas quais fenômenos aleatórios, acaso e incerteza estão presentes (Bennett, 2003; Everitt, 1999).

Surge, então, a necessidade de educar os alunos nesta área desde tenra idade, a fim de ter cidadãos probabilisticamente alfabetizados, capazes de lidar com uma ampla gama de situações do mundo real que envolvem a interpretação ou geração de mensagens probabilística, bem como a tomada de decisões (Gal, 2005).

Com relação ao programa de ensino desenvolvido por Bryant e Nunes (2012), este foca dois aspectos: (1) de um lado preocupa-se em promover a compreensão das crianças sobre os conceitos de aleatoriedade, avaliando a melhora da capacidade delas de resolver problemas matemáticos em situações que envolvam incerteza; (2) de outro, promover a compreensão das crianças sobre operações numéricas em um contexto em que se pode ter certeza dos resultados e, a partir daí, avaliar se o entendimento das ideias matemáticas que envolvem certeza pode contribuir e melhorar também o seu conhecimento de Probabilidade (Tonouti, 2013).

Vale salientar que este programa de ensino contempla alguns dos elementos descritos no modelo de letramento probabilístico proposto por Gal (2005), relacionados ao tratamento da aleatoriedade, cálculos probabilísticos e questões críticas.

Na Figura 1, apresentamos o esquema desse programa de ensino que inicia nas ideias mais simples sobre aleatoriedade, passa pela quantificação de probabilidades e chega até o entendimento do risco (associação entre variáveis).

 

Figura 1

Etapas do programa de ensino sobre probabilidade e risco

Fonte: Bryant e Nunes (2012)

 

Em relação à primeira unidade do programa de estudo, a aleatoriedade, Bryant e Nunes (2012) indicam que nas situações de caráter probabilístico em que um conjunto de eventos possíveis pode acontecer, é presumível de se encontrar dificuldades em crianças com essas situações. Esse problema encontrado é explicado pela dificuldade em identificar no conjunto de eventos possíveis, quais deles vão acontecer ou em que ordem acontecem, sendo devido à aleatoriedade, pois não é possível determinar a forma com que os eventos ocorrem numa sequência ou num arranjo espacial aleatório.

Na segunda unidade da proposta de Bryant e Nunes (2012) é abordado o conceito de Espaço Amostral que é o conjunto de todos os eventos possíveis que têm um papel que não pode ser subestimado nos processos de ensino e aprendizagem da probabilidade. Indica-se a necessidade em identificar o espaço amostral em qualquer tarefa para compreender e calcular as probabilidades de eventos específicos.

Bryant e Nunes (2012) descrevem que na unidade de quantificação de probabilidades, busca-se calcular a probabilidade ou comparar a força de duas ou mais probabilidades constituindo-se na etapa final da solução de um problema. Estes cálculos são de naturezas proporcionais desde que cada probabilidade seja a proporção entre um resultado específico e o conjunto de resultados possíveis.

Segundo Bryant e Nunes (2012), a correlação é uma forma de raciocínio envolvido na determinação da natureza e da força de uma relação mútua entre duas variáveis exigindo o reconhecimento de que as relações entre variáveis não são absolutas, mas existem em graus e envolvendo o raciocínio probabilístico. Atividades de comparação de um sucesso em um experimento aleatório podem ser trabalhadas com as crianças para desenvolver um melhor raciocínio probabilístico.

Neste processo de reestruturação do jogo, além da BNCC (Ministério da Educação, 2018) e do Programa de ensino sobre probabilidade e risco de Bryant e Nunes (2012), como já mencionamos, agregamos o documento GAISE II (Bargagliotti et al., 2020) por incorporar habilidades necessárias para entender os avanços relacionados ao ensino de estatística nos últimos 15 anos, mantendo o espírito do GAISE I (Franklin et al., 2007).

O GAISE II destaca, dentre os diversos aspectos relacionados ao ensino de estatística, o papel do pensamento probabilístico na quantificação da aleatoriedade em todos os níveis de ensino da Educação Básica ou como o próprio documento estabelece, ou seja, nos níveis A, B e C. Os alunos no Nível A devem desenvolver ideias informais de como a probabilidade está ligada ao raciocínio estatístico. Essas ideias ajudarão a apoiá-los quando mais tarde usarem probabilidade para fazer inferências informalmente no Nível B e mais formalmente no Nível C (Bargagliotti et al., 2020).

No jogo “Probabilidade em Ação”, o desenvolvimento dessas ideias informais de como a probabilidade está ligada ao raciocínio estatístico pode ser trabalhado por meio das cartas tipo “Saiba Mais”, visto que, quando o aluno se deparar com essas cartas, terá acesso a diferentes informações que abrangem diversas áreas do conhecimento, sendo possível observar sua compreensão, intervir e explorar o conteúdo, contribuindo com o desenvolvimento dessas primeiras ideias e assim ir avançando para os outros níveis.

Em Bargagliotti et al. (2020), indica-se que a probabilidade é sobre quantificar a aleatoriedade. É a base de como fazemos previsões em estatísticas. Começando em tenra idade, os alunos podem usar a probabilidade informalmente para prever quão prováveis ou improváveis podem ser determinados eventos. Eles também podem considerar previsões informais além do escopo dos dados que analisaram. Além disso, a probabilidade é uma ferramenta essencial em estatística, bem como na matemática, que emprega abordagens e raciocínios diferentes dos usados na estatística.

Dois problemas e a natureza das soluções ilustrarão a diferença, segundo Bargagliotti et al. (2020):

Problema 1: Suponha que um dado seja “justo”.

Pergunta: Se um dado for lançado 10 vezes, quantas vezes veremos um número par na face superior?

Problema 2: Você pega um dado.

Pergunta: Este é um dado justo? Ou seja, cada face tem a mesma chance de aparecer?

O problema 1 é um problema de probabilidade matemática. O Problema 2 é um problema de estatística que pode usar o modelo matemático de probabilidade determinado no Problema 1 como ferramenta para buscar uma solução. (p. 10)

Em Bargagliotti et al. (2020) destacamos quais são os aspectos a serem considerados em cada um dos três níveis (A, B e C) para o ensino de probabilidade, diretamente associado ao ensino de estatística. O Tabela 2 apresenta estas características.

 

Tabela 2

Estrutura conceitual para o ensino de probabilidade segundo o documento norte-americano GAISE II

Nível	Descrição
A	Os alunos devem começar a entender que a probabilidade é uma medida da chance de que algo aconteça. É uma medida do grau de certeza ou incerteza. A probabilidade de eventos deve ser vista como estando em um continuum do impossível ao certo, com menos provável, igualmente provável e mais provável. Usando essas noções probabilísticas, os alunos do Nível A podem elaborar sua resposta à pergunta investigativa estatística para incluir declarações como: Se um aluno da nossa classe for selecionado aleatoriamente, é mais provável que ele seja um aluno que prefira Rap, Country ou Rock?
B	Deve-se reconhecer que, embora a amostra combinada seja maior, ela ainda pode não ser representativa de toda a população (ou seja, todos os alunos de sua escola). Em estatística, aleatoriedade e probabilidade são incorporadas ao procedimento de seleção da amostra para fornecer um método que seja “justo” e para melhorar as chances de selecionar uma amostra representativa. Por exemplo, se a turma decidir selecionar o que é chamado de amostra aleatória simples de 54 alunos, então cada amostra possível de 54 alunos terá a mesma probabilidade de ser selecionada. Esta aplicação ilustra um dos papéis da probabilidade na estatística. Embora os alunos não possam realmente empregar um procedimento de seleção aleatória ao coletar dados no Nível B, questões relacionadas à obtenção de amostras representativas devem ser discutidas.
C	Faz com que os alunos passem por estatísticas descritivas de todo o grupo ou população para incorporar noções de chance e probabilidade para fazer inferências gerais e comparações inferenciais sobre dois grupos. As simulações são empregadas para aprimorar o raciocínio probabilístico. Os alunos compreendem a variabilidade amostra a amostra.

Fonte: Bargagliotti et al. (2020, pp. 27; 49; 72)

 

Partindo dos princípios apresentados nos três níveis do documento consideramos que convergem em vários sentidos, principalmente no que se refere à verbalização por parte dos alunos em relação às suas análises, considerando que essa ação é fundamental para o entendimento das primeiras noções probabilísticas.

Na BNCC (Ministério da Educação, 2018) e no programa de ensino desenvolvido por Bryant e Nunes (2012), o ensino de probabilidade parte das ideias mais simples sobre aleatoriedade e, de forma gradativa, segue para a compreensão e determinação do espaço amostral e consequentemente para a identificação dos diversos eventos aleatórios que são subconjuntos do espaço amostral. Destacam a necessidade e importância do aluno em distinguir os diferentes tipos de eventos aleatórios, bem como os termos e o significado desses termos.

Essas ideias se coadunam com o documento GAISE II ao afirmar que a probabilidade é uma ferramenta essencial na medida em que os alunos podem utilizá-la de maneira não-formal para indicar quão prováveis podem ser determinados eventos, considerando que é o ponto de partida para a compreensão de que a probabilidade está ligada ao raciocínio estatístico.

O raciocínio estatístico, segundo Pfannkuch (2018), define o modo com que os indivíduos raciocinam com as ideias estatísticas e dão sentido à informação estatística, tendo subjacente a compreensão conceitual e a conexão de importantes ideias, como variação, distribuição, centro, dispersão, associação e amostragem ou a combinação de ideias sobre dados e incerteza que conduzem à realização de inferência.

 

3. METODOLOGIA

 

A reestruturação do jogo “Probabilidade em Ação” foi embasada na metodologia de design iterativo proposta por Zimmerman (2003), pensada para o desenvolvimento de jogos digitais, mas, também se adequando aos jogos físicos por se tratar de um processo iterativo e cíclico de testes e ajustes.

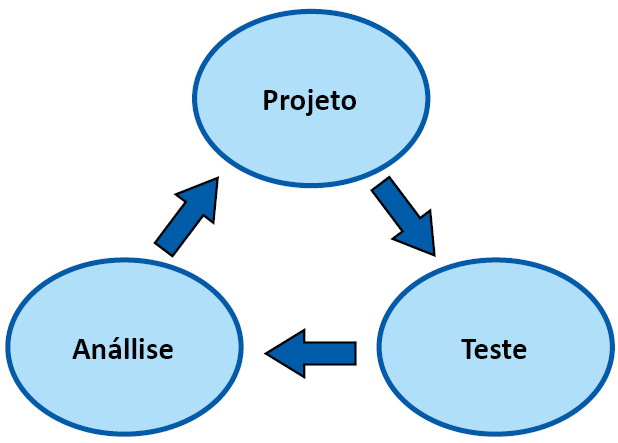
Nesta metodologia as decisões de design são baseadas na experiência do protótipo em andamento que é testado e revisado quantas vezes forem necessárias, num processo, de forma que venha a se desenvolver por um diálogo contínuo entre os designers, design e o público teste (Figura 2).

 

Figura 2

Modelo do design iterativo

Fonte: Traduzido de Zimmerman (2003, p. 1)

 

Para Zimmerman (2003), no caso de jogos, design iterativo significa teste de jogo. Durante todo o processo de design e desenvolvimento, seu jogo é jogado. Em cada caso, você os observa, faz perguntas, depois ajusta seu design e testa novamente.

O processo iterativo de design é radicalmente diferente do desenvolvimento típico de jogos a varejo, pois na maioria das vezes o processo desses jogos se inicia com um título e se pensa num conceito final, escrevendo logo em seguida um documento exaustivo que descreve todos os aspectos possíveis do jogo em detalhes. Invariavelmente, o jogo final nunca se assemelha ao original. Já um processo de design mais iterativo não apenas agilizará os recursos de desenvolvimento como também resultará em um produto final mais robusto e bem-sucedido (Zimmerman, 2003).

Zimmerman (2003) indica que se deve no processo de elaboração de um jogo, testar, analisar e refinar. Esse processo deve se repetir tantas vezes quanto for necessário porque a experiência de um espectador/usuário/jogador nunca pode ser completamente prevista. O protótipo é testado, revisões são feitas e o projeto é testado mais uma vez.

Assim desde o início do processo de construção do jogo “Probabilidade em Ação” uma série de protótipos foram criados, sendo um processo contínuo com idas e vindas, testes e ajustes, até chegar a um protótipo mais elaborado, que também passará por testes.

 

4. O PROCESSO DE DESIGN ITERATIVO DO JOGO DE TABULEIRO DENOMINADO “PROBABILIDADE EM AÇÃO”

 

Ao longo do processo de construção e reconstrução do jogo, vários protótipos foram criados, testados e analisados. Datori Barbosa (2019) sustentou a ideia de criar um jogo de tabuleiro com percurso para os desafios, que a princípio envolveria conceitos probabilísticos e estatísticos.

O primeiro modelo de tabuleiro, que neste trabalho chamamos de protótipo devido à metodologia utilizada, foi feito em aquarela no papel cartão. Tanto o layout como o conteúdo pedagógico do jogo abordavam conceitos de probabilidade e de estatística. Para percorrer o tabuleiro foram criados dois bonequinhos em biscuit, um representando Karl Pearson e outro, Ronald Fisher (Figura 3).

 

Figura 3

Primeiro tabuleiro confeccionado em aquarela e papel cartão

Devido a quantidade de objetos de conhecimento envolvido nas cartas do jogo (Probabilidade e Estatística), esse modelo inicial foi alterado, podendo ser identificado em Datori Barbosa (2019) e Oliveira Júnior e Datori Barbosa (2020), na qual foi sugerido delinear a pesquisa com foco na probabilidade.

Analisando o protótipo elaborado, percebemos que o modelo não era viável em termos de reprodução para ser disponibilizado aos professores. Pensando num modelo de jogo que favorecesse o acesso e consequentemente a disponibilização para uso do professor em sala de aula, o jogo foi reconstruído no Power Point (programa utilizado para criação/edição e exibição de apresentações gráficas). Essa modificação pode ser visualizada na Figura 4.

 

Figura 4

Protótipo construído no Power Point

Nesse processo de reestruturação do jogo, embora tenhamos mantido os bonequinhos de biscuit no trabalho para representar os jogadores, foi aberto espaço para troca por marcadores coloridos. Ainda, para que se possa percorrer o tabuleiro indicamos a utilização de um dado comum (Figura 5).

Figura 5

Dado e pinos para o jogo “Probabilidade em Ação”

Ressaltamos que os jogos com dados (ou objetos similares) existem desde o Egito Antigo e fazem parte da história da Probabilidade desde muito antes dessa área se consolidar dentro da Matemática. Lopes e Meirelles (2005) dizem que a teoria da probabilidade apareceu como ramo da Matemática em meados do século XV, embora tenha se iniciado como ciência empírica muito antes desse período. Indicam ainda que suas raízes apareceram principalmente nos jogos e apostas, havendo registros de que, por volta do 1200 a.C., um pedaço de osso do calcanhar (Astragalus), Figura 6, fosse utilizado formando faces como as de um dado. E, mesmo antes disso, por volta de 3500 a.C., no Egito, já havia jogos utilizando ossinhos. Os romanos também eram apaixonados por jogos de dados e cartas que, durante a Idade Média, foram proibidos pela Igreja Cristã.

 

Figura 6

Imagem de um Astrágalo

Fonte: Disponível em: <http://www.ancienttouch.com/1081.jpg>. Acesso em: 17 jun. 2022

 

O jogo apresentado neste trabalho, como já exposto acima, é composto por dois tipos de cartas: (1) Perguntas (?) referindo-se às situações problemas que devem ser respondidas para caminhar no tabuleiro; e (2) Saiba Mais (!), que trazem curiosidades e/ou informações probabilísticas.

Neste processo de reestruturação e prototipagem, após diversos testes e análises, algumas implementações foram realizadas em relação as cartas do jogo. Por exemplo, nas cartas tipo “Saiba Mais”, partindo das informações que em Datori Barbosa (2019) eram apresentadas somente pela representação percentual, essa foi ampliada para uma linguagem verbal, fracionária e decimal. Dessa forma, refletindo-se sobre seu objetivo no jogo e atendendo ao que a BNCC (Ministério da Educação, 2018) indica, foram trazidas informações para as crianças mostrando que a Probabilidade está associada a discussões em diversas áreas do conhecimento e em diferentes contextos (Figura 7).

 

Figura 7

Modelos de cartas ‘Saiba +”

Este ajuste ocorreu após nos colocarmos no lugar do jogador “aluno”, ou seja, de acordo com Zimmerman (2003), o jogo deve ser jogado, observado, questionado e ajustado num processo cíclico que perdura todo o seu desenvolvimento. Assim, após observar e questionar as informações probabilísticas contidas nas cartas do jogo, percebemos que seria muito mais enriquecedor utilizar diversos tipos de linguagem no lugar de utilizar uma única linguagem (percentual). Ainda, os diferentes tipos de linguagens estabeleceriam uma conexão mais direta com a unidade temática “Números e Operações”.

Quanto às cartas tipo “Perguntas”, relembramos que, inicialmente, a elaboração das situações problemas (também chamadas de tarefas em Datori Barbosa, 2019) buscou-se conectar à BNCC (Ministério da Educação, 2018) e ao Programa de Ensino desenvolvido por Bryant e Nunes (2012), desenvolvido na Inglaterra para ser aplicado nos anos iniciais da Educação Básica, de forma a possibilitar também um diálogo com pesquisas realizadas na área de probabilidade, bem como as propostas de Coutinho (2001), Batanero e Godino (2002) e Gal (2005).

Apoiados pela metodologia de Zimmermann (2003), essas cartas ganharam um novo design no layout, com opções coloridas em consonância com o conteúdo escrito e ainda, a inserção da proposta do documento norte-americano denominado GAISE II (Bargagliotti et al., 2020), focando em situações problemas que estivesses associadas a experimentos que podem ser pensados durante o jogo.

Ressaltamos que as opções de resposta em Datori Barbosa (2019) não eram coloridas sendo esse um processo em que novos modelos de layout foram surgindo até chegar no modelo atual. Justificando essa mudança no layout, no modelo anterior ao atual (Figura 8) as cartas eram coloridas em tons claros, mas sem preocupação com o conteúdo escrito e/ou espaço amostral.

Entretanto, ao aplicar a metodologia do design iterativo esse modelo foi alterado, visto que após testarmos o jogo, observando uma criança jogando, foi possível perceber que quando a cor das opções de resposta se diferenciava do conteúdo escrito e/ou do espaço amostral gerava confusão e muitas vezes erros na escolha da resposta. Diante desta observação ajustamos as cores das opções das cartas de acordo com o conteúdo escrito e/ou espaço amostral (Figura 8), mantendo as cores em tons claros para as cartas em que a escrita e/ ou o espaço amostral não são influenciados pela cor.

 

Figura 8

Modelos de cartas Pergunta (anterior ao atual e atual)

A reestruturação do jogo finalizou com a implementação de customização das cartas “Perguntas” e “Saiba Mais”. Analisando todas as cartas que foram criadas, sentiu-se a necessidade de criar possibilidades de renovação das mesmas. Assim, criou-se um template (Figura 9) onde o próprio professor pode elaborar novas cartas de acordo com o objeto de conhecimento que está trabalhando ou de acordo com a dificuldade dos alunos e/ou ainda, propor aos alunos que eles mesmos, em grupo, criem situações problemas para serem acopladas ao jogo.

 

Figura 9

Template para criar as cartas

Esta ideia de customização partiu de observações e questionamentos que tiveram por objetivo potencializar o trabalho em sala de aula em prol do desenvolvimento do raciocínio probabilístico, oferecendo ao professor uma ferramenta de ensino passível de ser reutilizada, podendo ser renovada ou modificada, dependendo de sua intencionalidade.

Para finalizar, foi criado um “cartão resposta” (Figura 10) para ficar em posse do “juiz” do jogo, uma pessoa (aluno), que será incumbido de indicar se a resposta dada pelos jogadores está correta ou não, para então o peão percorrer ou não o tabuleiro.

 

Figura 10

Cartão resposta

 

Segundo proposta de Datori Barbosa (2019) a respeito da organização e das regras do jogo, essas foram mantidas, considerando-se que em relação à organização, os alunos podem ser divididos em grupos compostos por, no mínimo dois e no máximo quatro integrantes. As regras do jogo são as seguintes:

1. Para iniciar o jogo os personagens deverão ser posicionados na casa “Início” e logo em seguida os grupos lançarão o dado para determinar quem iniciará a partida.

2. O grupo que obtiver o maior número no lançamento do dado começa a partida pegando uma carta do monte das “perguntas” (?), da qual um dos componentes irá ler em voz alta para o grupo responder.

3. O grupo respondendo acertadamente à questão, deverá avançar no tabuleiro a quantidade de casas indicada no valor obtido no lançamento do dado.

4. Caso o grupo erre a questão não poderá mover a peça do lugar e o outro grupo terá o direito de responder à pergunta, das quais acertando poderá avançar o total de casas correspondentes à questão.

5. Caso os dois grupos não acertem a solução do problema, havendo a possibilidade, o professor poderá intervir no jogo com perguntas que auxiliem os alunos na busca da solução, de forma que juntos percebam os “erros” cometidos;

6. Sempre que o personagem cair na casa “pergunta” (?), uma carta desse monte deverá ser retirada e esse processo se repete.

7. Quando o personagem representante do grupo cair na casa “Saiba Mais” (!), alguém do grupo deverá também ler em voz alta, para que todos ouçam, e em seguida, andar uma casa no tabuleiro.

8. Após andar uma casa, será a vez do outro grupo jogar.

9. No caso de retornar a mesma casa com questões que indiquem informações para enriquecer o conhecimento, representada por “!”, o grupo não deverá retirar outra carta “Saiba Mais”, mas sim, manter-se na casa e aguardar a próxima rodada para continuar jogando.

10. Quando o personagem representante do grupo cair na casa “Avance casas” (+1), (+2), deverá avançar a quantidade de casas correspondentes, da mesma forma, se cair na casa “Retornar casas” (-1), (-2), deverá retornar à quantidade de casas correspondentes;

11. Ganha a partida o grupo que chegar primeiro ao final do tabuleiro, ou seja, na casa “Fim”.

Posteriormente à elaboração das tarefas (situações problemas) contidas nas cartas tipo “Perguntas” do jogo, ela foi e continua fundamentada na Teoria Antropológica do Didático (TAD) de Chevallard (1996), o que permitiu uma análise praxeológica matemática e didática sobre essas tarefas, ampliando o olhar em cada uma delas, desde as possíveis estratégias práticas para resolução da tarefa até o discurso teórico-tecnológico acerca dessas estratégias.

Esse processo obedeceu fundamentalmente aos seguintes aspectos: (1) Apresentar pelo menos uma técnica para resolver tarefas solicitadas; (2) Para as técnicas descritas estabelecer, pelo menos, um esboço de um discurso tecnológico; (3) Articular diversos tipos de tarefas em torno dos conceitos probabilísticos; (4) Articular diversos tipos de tarefas utilizando a metodologia da resolução de problemas. Especificamente em relação ao conceito e espaço amostral, o intuito foi que os alunos reconhecessem como representar todas as possibilidades que podem ser listadas a partir da proposta de um problema voltado a situações, que podem inclusive vir a ser experimentadas em sala de aula.

Considerando o design iterativo proposto por Zimmerman (2003), destacamos que inicialmente os próprios pesquisadores participaram efetivamente do processo de criação do jogo “Probabilidade em Ação” e das cartas (Respostas e Saiba Mais). Ademais, criamos um momento para que 21 professores avaliassem o jogo em sua participação em curso de extensão que foi ofertado pelo Grupo de Estudos em Educação Estatística e Matemática - GEEM da Universidade Federal do ABC - UFABC denominado “Formação de professores a partir de um jogo pedagógico para o ensino de probabilidade nos anos iniciais do Ensino fundamental”.

Destacamos que o jogo é uma possibilidade lúdica que visou trazer aspectos motivacionais, pensando nesse como pretexto para o ensino de conceitos probabilísticos, mas não de contexto, visto que a resolução de problemas está nas cartas do jogo e não no jogo em si. Dessa forma, pode-se responder e utilizar as propostas (cartas) do jogo tanto durante o jogo como fora do jogo.

Segundo Bittar (2017), o modelo praxeológico proposto para descrever qualquer atividade, matemática ou não, é composto por: tipo de tarefas T; técnicas (τ) que resolvem as tarefas desse tipo; tecnologia (τ) que justificam as técnicas e garantem sua validade, e, finalmente, a teoria (Θ) que justifica a tecnologia. Esse quarteto praxeológico é denotado [T, τ, 𝜃, Θ], sendo que o bloco [T, τ] é denominado de prático-técnico (práxis), ou bloco do saber-fazer; e o bloco [𝜃, Θ] é denominado bloco tecnológico-teórico (logos) ou bloco do saber.

Assim, como exemplo, a carta mostrada na Figura 11, buscou determinar o espaço amostral por meio de experimentos, isto é, indicar todos os pares de bolas, sem reposição, de uma caixa contendo seis bolas, sendo três brancas e três pretas.

 

Figura 11

Uma das cartas do jogo sobre espaço amostral

A técnica utilizada indica que a resposta à tarefa proposta é a opção “C”, que é expressa por todos os resultados possíveis do experimento aleatório, ou seja, designar todas as maneiras possíveis de sair duas bolas, entre seis bolas (três brancas e três pretas) retiradas ao acaso e sem reposição. Cabe destacar que a ordenação das duas bolas faz diferença na resposta do problema. Dessa forma temos o seguinte espaço amostral S = {ll; ll;ll ;ll}. Ainda indicamos que as opções “A”, “B” e “D” não são os resultados possíveis, pois não apresentam todas as possíveis ordenações e, consequentemente, indicam alguns eventos, subconjuntos do espaço amostral, e não especificamente o espaço amostral S.

O discurso teórico-tecnológico (θ1, Θ1), que permite justificar e explicar a técnica pode ser inicialmente descrito por Pacto Nacional pela Alfabetização na Idade Certa - PNAIC (Ministério da Educação, 2014), destacando a importância do conceito de espaço amostral, indicando que as crianças necessitam compreender as possibilidades de um espaço amostral, sendo importante que desenvolvam um esquema para conseguir mapear todas as combinações possíveis do experimento aleatório sem esquecer nenhuma e nem tampouco repetir alguma.

Abordando a praxeologia didática para o ensino de probabilidade o objetivo da tarefa está relacionado à habilidade (EF05MA22) da BNCC (Ministério da Educação, 2018), que indica apresentar todos os possíveis resultados de um experimento aleatório, estimando se esses resultados são igualmente prováveis ou não. A tarefa configura-se em que os jogadores/alunos ampliem a ideia de espaço amostral. Finalizando, ressaltamos que todas as cartas do jogo com as análises praxeologias matemáticas e didáticas podem ser consultadas em Datori Barbosa (2019).

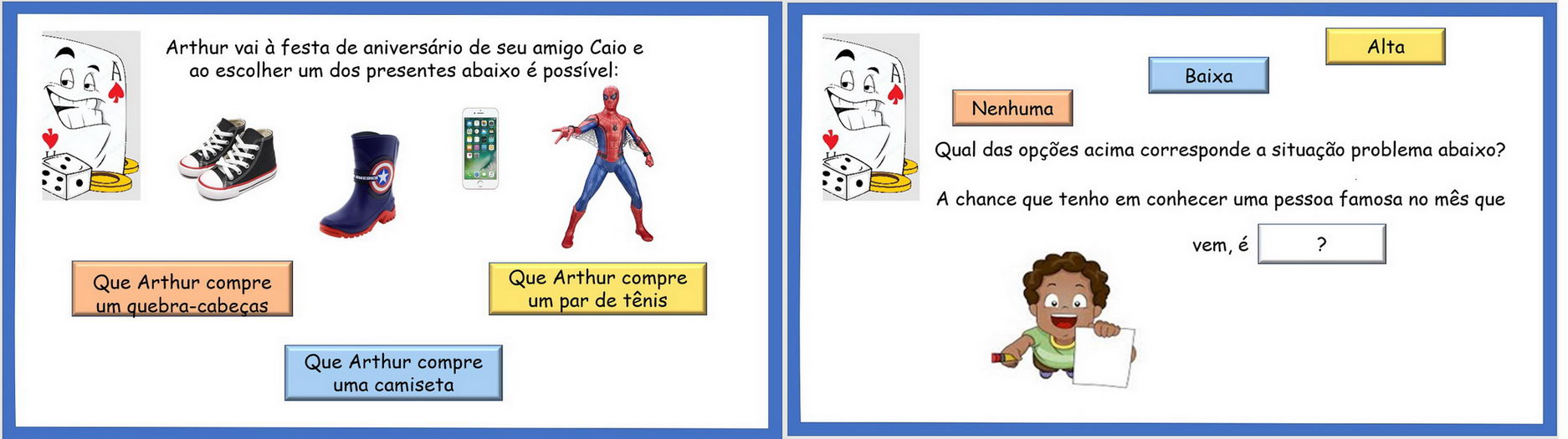
Ademais, na Figura 12, apresentamos mais duas tarefas como exemplos de diferentes abordagens de conceitos e situações probabilísticas, indicando, respectivamente, cartas do jogo sobre a identificação de evento aleatório possível e sobre a chance de ocorrência de um evento.

Considerando a primeira carta da Figura 12, buscou-se abordar a primeira unidade (aleatoriedade) do programa de ensino sobre probabilidade e risco de Bryant e Nunes (2012) e as habilidades segundo a BNCC para o terceiro ano do ensino fundamental brasileiro, ou seja, analisar a ideia de acaso em situações do cotidiano (espaço amostral), identificando, como eventos familiares aleatórios podem ser associados a todos os resultados possíveis e, consequentemente, estimar os que têm maiores ou menores chances de ocorrência (Ministério da Educação, 2018).

 

Figura 12

Cartas do jogo sobre a identificação de evento aleatório possível e sobre a chance de ocorrência de um evento

 

Trazendo análise praxeológica, de acordo com a situação proposta, deve-se refletir sobre o problema em questão e com base na observação do espaço amostral, determinar qual das opções listadas é possível. Para tanto será preciso refletir sob que circunstâncias um evento é considerado possível e a partir de análises sobre as condições e o contexto de cada um, identificar dentre as opções elencadas qual evento tem chances de ocorrência.

No caso da segunda carta da Figura 12, abordou-se a terceira unidade (quantificação de probabilidades) do programa de ensino sobre probabilidade e risco de Bryant e Nunes (2012) e as habilidades segundo a BNCC para o quarto ano do ensino fundamental brasileiro, ou seja, analisar chances de eventos aleatórios, identificando, entre eventos aleatórios cotidianos, aqueles que têm maior chance de ocorrência, reconhecendo características de resultados mais prováveis, sem utilizar frações (Ministério da Educação, 2018).

A tarefa proposta indica uma situação, na qual o aluno terá que analisar se esse evento aleatório possível se classifica como de nenhuma, baixa, ou alta chance de ocorrência. Para tanto será preciso refletir sobre a condições e o contexto, de forma a enquadrá-la a uma das opções elencadas. Considera-se que a resposta para o problema proposto é a opção “B”, visto que a chance de que este evento ocorra não é impossível e nem certo, mas é possível, apesar de poder se configurar como improvável.

No caso das duas cartas indicadas, o discurso teórico-tecnológico que permite justificar e explicar a técnica pode ser explicitado segundo MOOC (2017), quando diz que o termo probabilidade é usado diariamente, embora nem sempre com a precisão matemática necessária. Em linguagem comum, o conceito de provável está associado ao de possível, isto é, diz-se que um fato é provável de ocorrer se houver a possibilidade de que ele realmente ocorra. No entanto, isso pode ser ambíguo e uma conotação matemática mais precisa é necessária. Caso você tenha um espaço amostral com n pontos de amostragem, para os quais não há preferência de ocorrência, então é dito que os pontos de amostragem são igualmente possíveis ou igualmente prováveis (ou equiprováveis). Por exemplo, quando um dado “honesto” numerado de um a seis é lançado, presume-se que os seis desfechos possíveis sejam igualmente prováveis ou equiprováveis.

Ainda foi pensando nas duas situações indicadas, além de todas que compõem as cartas do jogo, trazer situações que podem ser vivenciadas pelos alunos e que se configuram como aleatórias, além de permitir ser trabalhado o processo investigativo.

Por fim, trazemos uma breve discussão, tomando como base a BNCC, o GAISE II e o programa de Ensino de Probabilidade e Risco proposto por Bryant e Nunes, além do PNAIC, que fundamentaram a construção das cartas do jogo e que ainda permitirão que professores possam elaborar outras cartas.

Nesse sentido, no Caderno 7 do PNAIC direcionado à Educação Estatística (Ministério da Educação, 2014), propõe-se pensar em material didático que vise inserir a criança no universo da investigação. Considera-se fundamental na atitude investigativa a preocupação em formular questões, elaborar hipóteses, escolher amostra e instrumentos adequados para a resolução de problemas e para a tomada de decisão.

Ainda indicamos que no documento GAISE II (Bargagliotti et al., 2020) é reforçado que a análise de dados é um processo investigativo que envolve: 1) Realizar suas próprias perguntas (esclarecer o problema em questão e formular questões que possam ser respondidas com dados); 2) Coletar informações apropriadas de várias fontes. Desenhar um plano apropriado para coletar dados e os empregar; 3) Analisar as informações por meio de métodos gráficos e numéricos apropriados e os utilizar para analisar os dados; 4) Interpretar os resultados, com o objetivo de inferir uma população com base em uma amostra, relacionando com a pergunta original.

A apresentação, por exemplo, da carta indicada na Figura 11, focando no conceito de espaço amostral, apesar de estar relacionada especificamente à segunda unidade do programa de ensino sobre probabilidade e risco de Bryant e Nunes (2012), perpassa pela primeira unidade, quando considera a ocorrência do conjunto de eventos possíveis, no caso o próprio evento certo, indicando a necessidade de que o aluno possa identificar o espaço amostral em qualquer tarefa, elemento essencial para a proposta das unidades seguintes, quais sejam, compreender e calcular as probabilidades de eventos específicos.

Por fim, destacamos que na BNCC (Ministério da Educação, 2018), indica-se que a incerteza e o tratamento de dados devem ser estudados na educação básica brasileira, propondo a abordagem de conceitos, fatos e procedimentos que estejam presentes em situações-problema da vida cotidiana dos alunos. Assim, todos os cidadãos precisam desenvolver habilidades para coletar, organizar, representar, interpretar e analisar dados em uma variedade de contextos, de maneira a fazer julgamentos bem fundamentados e tomar decisões adequadas.

 

5. CONSIDERAÇÕES FINAIS

 

Com o olhar voltado tanto para a proposta da BNCC (Ministério da Educação, 2018) acerca das competências a serem desenvolvidas nos anos iniciais, bem como para a necessidade de uma análise prática e teórica mais aprofundada dos objetos de conhecimento probabilísticos envolvidos na elaboração das cartas à luz da TAD, acreditamos que o jogo “Probabilidade em Ação” poderá ser utilizado por professores como ferramenta de ensino.

Em relação ao processo de reconstrução do jogo consideramos que a utilização da metodologia do design iterativo contribuiu para o seu aprimoramento, visto que os ajustes foram realizados devido aos testes, as observações e as análises realizadas.

Em nossa leitura, acreditamos que o jogo de tabuleiro “Probabilidade em Ação” apresenta alguns aspectos educativos importantes. O primeiro deles é com relação as casas “Perguntas” (?), em que a maior parte das situações problemas podem e “devem” ser simuladas em sala de aula para que o aluno possa vivenciar alguns experimentos.

Um segundo aspecto a ser apontado refere-se às cartas “Saiba Mais” (!). Essas cartas trazem informações probabilísticas por meio de diferentes representações (linguagem verbal, linguagem numérica em fração, decimal e percentual), abarcando diversas áreas do conhecimento, mostrando que a probabilidade não se limita ao campo matemático. Essas diferentes formas de representar graficamente as informações probabilísticas viabiliza conexão com outros eixos matemáticos, neste caso, com o eixo “Números e Operações”.

O terceiro aspecto é com relação a criação do template, que consideramos ser um pretexto estratégico, isto é, uma inovação do jogo de caráter motivacional e reflexivo para ser trabalhado com os alunos em sala de aula. Motivacional, porque as cartas criadas passarão a fazer parte do jogo e reflexivo porque para criar as cartas, tanto “perguntas” como “Saiba Mais”, será necessário refletir sobre uma situação que envolva conceitos de probabilidade e problematizar essa situação, com base em discussões e trocas de ideias de um conhecimento prévio ou já adquirido.

O quarto aspecto é mais de cunho didático e referente à dinâmica do jogo, em que o professor poderá observar e interagir com o pensamento probabilístico do aluno para:

1. Observar a forma como seus alunos pensam, agem, interagem e argumentam;

2. Descobrir quais conhecimentos prévios possuem;

3. Analisar a linguagem e os termos que utilizam e se entendem o significado desses termos;

4. Perceber suas maiores dificuldades e facilidades;

5. Mediar e intervir, quando necessário, nas situações decorrentes do jogo, visando contribuir com a aprendizagem do aluno;

6. Articular os objetos de conhecimento apresentados no jogo com a realidade do aluno para alcançar uma aprendizagem significativa.

Assim, reconhecemos que o caráter lúdico do jogo estimula a participação e a troca de conhecimentos entre alunos e professores e entre alunos, pois abre espaço para verbalizarem suas ideias e resolverem problemas envolvendo o acaso de maneira espontânea e descontraída.

Neste viés, acreditamos que o jogo “Probabilidade em Ação” apresenta potencial para ser considerado uma ferramenta de ensino que poderá auxiliar alunos e professores nos processos de ensino e aprendizagem da probabilidade nos anos iniciais do Ensino Fundamental.

 

REFERÊNCIAS BIBLIOGRÁFICAS

 

Bargagliotti, A., Franklin, C., Arnold P., Gould, R., Johnson, S., Perez, L. e Spangler, D.A. (2020). Pre-K–12 Guidelines for Assessment and Instruction in Statistics Education II (GAISE II)? A Framework for Statistics and Data Science Education Writing Committee. ASA. https://www.amstat.org/docs/default-source/amstat-documents/gaiseprek-12_full.pdf

Batanero, C. e Godino, J.D. (2002). Estocástica y su didáctica para maestros. Departamento de Didáctica de la Matemática, Universidad de Granada.

Bennett, D.J. (2003). Aleatoriedade. Martins Fontes.

Bittar, M.A. (2017). Teoria Antropológica do Didático como ferramenta metodológica para análise de livros didáticos. Zetetiké, 25(3), 364-387.

Bryant, P. e Nunes, T. (2012). Children’s understanding of probability: a literature review (full report). Nuffield Foundation.

Chevallard, Y. (1996). Conceitos fundamentais da didáctica: perspectivas trazidas por uma abordagem antropológica. In J. Brun (Ed.), Didáctica das Matemáticas (pp. 115-153). Horizontes Pedagógicos.

Coutinho, C.Q.S. (2001). Introduction aux situations aléatoires dès le Collège: de la modélisation à la simulation d’expériences de Bernoulli dans l’environnement informatique Cabri-géomètre II. [Tese de Doutorado em Didática da Matemática, Université Joseph Fourier, Grenoble I]. Biblioteca Digital de Teses e Dissertações PUC Minas. https://www.pucsp.br/~cileda/theseCileda.PDF

Datori Barbosa, N. (2019). O trilhar da construção de um jogo pedagógico como ferramenta para o ensino de probabilidade nos anos iniciais do ensino fundamental. [Dissertação de Mestrado em Ensino e História das Ciências e da Matemática, Universidade Federal do ABC]. Biblioteca Digital de Teses e Dissertações Sophia UFABC. https://biblioteca.ufabc.edu.br/

Everitt, B. S. (1999). Chance rules: an informal guide to probability, risk, and statistics. Springer.

Franklin, C., Kader, G., Mewborn, D., Moreno, J., Peck, R., Perry, M. e Scheaffer, R. (2007). Guidelines for Assessment and Instruction in Statistics I (GAISE I) Education: A Pre-K-12 Curriculum Framework. American Statistical Association. http://www.amstat.org/education/gaise/

Gal, I. (2005). Towards’ probability literacy for all citizens. In Jones, G. A (Ed.), Exploring probability in school: challenges for teaching and learning (pp. 39-63). Springer.

Godino, J.D., Batanero, C. e Cañizares, M.J. (1996). Azar y Probabilidad. Síntesis.

Grando, R.C., Laurent, A.A.V.K., Santos, R.S. y Grillo, R. (2022). A matemática possível nos jogos na Educação Infantil. In K.T. Ciríaco e C.A. Oliveira (Eds.), Tendências em educação matemática na infância (pp. 125-143). SBEM Nacional.

Instituto Avisa Lá. (8 de noviembre de 2021). Live com o Prof. Dr. Lino de Macedo e Érica Dutra [Archivo de Vídeo]. Youtube. https://www.youtube.com/watch?v=rhERHLLwIRM

Lopes, C.A.E. e Meirelles, E. (2005). Estocástica nas séries iniciais. Anais do 18 Encontro Regional de Professores de Matemática. LEM/IMECC/UNICAMP. https://www.ime.unicamp.br/erpm2005/anais/m_cur/mc02_b.pdf

Luckesi, C. (2014). Ludicidade e formação do educador. Revista Entreideias, 3(2), 13-23.

Ministério da Educação (2014). Secretaria de Educação Básica. Diretoria de Apoio à Gestão Educacional. Pacto Nacional pela Alfabetização na Idade Certa: Educação Estatística. Secretaria de Educação Básica.

Ministério da Educação (2018). Base Nacional Comum Curricular: Educação é a base. Conselho Nacional de Educação. http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf

MOOC. Estadística y probabilidad: probabilidad básica. Preparación Matemáticas Bachillerato – Educación Básica, material complementario, Costa Rica, 2017. MEP. http://www.reformamatematica.net/wp-content/uploads/2018/09/PMB-EP04_Probabilidad-ba%CC%81sica.pdf

Oliveira Júnior, A.P. e Datori Barbosa, N. (2020). O jogo pedagógico brincando com a probabilidade para os anos iniciais do ensino fundamental. Zetetiké, 28, 1-21.

Oliveira Júnior, A.P. e Datori Barbosa, N. (2023). Investigación sobre el uso de juegos manipulativos y digitales del 1° al 5° grado de la Enseñanza Fundamental para la enseñanza de la Probabilidad en Brasil. Revista Estudios Pedagógicos. (submetido à publicação).

Pfannkuch, M. (2018). Reimagining curriculum approaches. In D. Ben-Zvi, K. Makar e J. Garfield (Eds.), International Handbook of Research in Statistics Education (pp. 384-406). Springer International.

Silva, A.J.N. e Souza, P.S.S. (2021). Grupo de estudo e o movimento de ressignificação da concepção de ludicidade: uma experiência no LEPEM da UNEB. Brazilian Journal of Policy and Development, 3(3), 43-57.

Tonouti, R. R. (2013). Avaliação de um programa de ensino para a aprendizagem de probabilidade nos anos iniciais do ensino fundamental. [Dissertação de Mestrado em Educação Matemática, Universidade Bandeirante de São Paulo]. Repositório de Teses e Dissertações da Kroton.
https://repositorio.pgsskroton.com/handle/123456789/3641?locale=en

Zimmerman, E. (2003). Play as Research: the interactive design process. In B. Laurell (Ed.), Design Research: methods and perspectives (pp. 1-14). MIT Press. https://static1.squarespace.com/static/579b8aa26b8f5b8f49605c96/t/59921253cd39c3da5bd27a6f/1502745178453/Iterative_Design.pdf

 

Como citar:

Oliveira Júnior, A. P. y Datori Barbosa, N. (2023). Probabilidade em Ação: apresentando um jogo de tabuleiro para o ensino de probabilidade nos anos iniciais. Revista de Educación Estadística, 2(1), 1-25. https://doi.org/10.29035/redes.2.1.1

 

Esta obra está bajo una licencia de Creative Commons
Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional.