Revista de Educación Estadística https://revistaeduest.ucm.cl/ Vol. 2, n. 1, 1-28, abr. 2023 - sep. 2023 ISSN 2810-6164

 

DOI: https://doi.org/10.29035/redes.2.1.7

 

ESTRATEGIA PARA LA ENSEÑANZA DE LA INFERENCIA EN INGENIERÍA: FUNDAMENTOS PARA SU DISEÑO

Estratégia de ensino de inferência em engenharia: Fundamentos para seu projeto

Strategy for teaching inference in engineering: Foundations for its design

 

Stella Maris Figueroa*1

Universidad Nacional de Mar del Plata (Mar del Plata, Argentina)

María Laura Distéfano2

Universidad Nacional de Mar del Plata (Mar del Plata, Argentina)

 

Resumen

En este trabajo se presenta y fundamenta un diseño de actividades basado en ideas estadísticas fundamentales para la enseñanza de la inferencia, mediante la vinculación entre conceptos de estadística y de probabilidad, en la asignatura Estadística Básica de la Facultad de Ingeniería de la Universidad Nacional de Mar del Plata, Argentina. En esta propuesta didáctica, en una primera etapa, se utilizan los recursos de la inferencia estadística informal, a través de actividades que vinculan la teoría de probabilidades con la Estadística, para la comprensión de las ideas fundamentales de la estadística y, en una segunda etapa, se aplican técnicas de estimación y de pruebas de hipótesis para contrastar las conclusiones obtenidas previamente. De esta manera, el estudiante compara definiciones de conceptos análogos en el contexto teórico (probabilidad) y en el práctico (estadística), donde aplica la inferencia informal leyendo más allá de los datos, efectuando distintas representaciones y conjeturando sobre resultados muestrales, para luego confrontarlos, al resolver problemas de la inferencia formal. Se concluye que el diseño de este tipo de actividades proporciona al estudiante un hilo conductor que une todas las etapas del método estadístico y articula los conceptos probabilísticos y estadísticos utilizados.

Palabras clave: Enseñanza por competencias, Probabilidad, Estadística, Inferencia Estadística, Ingeniería.

 

Resumo

Este artigo apresenta e fundamenta um desenho de atividades baseadas em ideias estatísticas fundamentais para o ensino de inferência, através da ligação entre conceitos de estatística e probabilidade, na disciplina de Estatística Básica da Faculdade de Engenharia da Universidade Nacional de Mar del Plata, Argentina. Nesta proposta didática, em uma primeira etapa, são utilizados os recursos da inferência estatística informal, por meio de atividades que relacionam a teoria da probabilidade com a Estatística, para a compreensão das ideias fundamentais da estatística e, em uma segunda etapa, aplicam-se técnicas de estimação e hipóteses testes para contrastar as conclusões obtidas anteriormente. Dessa forma, o aluno compara definições de conceitos semelhantes no contexto teórico (probabilidade) e no prático (estatística), onde aplica inferência informal lendo além dos dados, fazendo representações diferentes e conjecturando sobre os resultados da amostra, para depois compará-los, para resolver problemas de inferência formal. Conclui-se que o desenho deste tipo de atividades proporciona ao aluno um fio condutor que une todas as etapas do método estatístico e articula os conceitos probabilísticos e estatísticos utilizados.

Palavras-chave: Ensino baseado em competências, Probabilidade, Estatística, Inferência estatística, Engenharia.

 

Abstract

This paper presents and substantiates a design of activities based on fundamental statistical ideas for the teaching of inference, through the link between concepts of statistics and probability, in the Basic Statistics subject of the Faculty of Engineering of the National University of Mar. del Plata, Argentina. In this didactic proposal, in a first stage, the resources of informal statistical inference are used through activities that link the theory of probability with Statistics for the understanding of the fundamental ideas of statistics and, in a second stage, they apply estimation techniques and hypothesis tests to contrast the conclusions previously obtained. In this way, the student compares definitions of similar concepts in the theoretical context (probability) and in the practical one (statistics), where he applies informal inference by reading beyond the data, making different representations and conjecturing about sample results to later compare them to the Solve formal inference problems. It is concluded that the design of this type of activities provides the student with a common thread that unites all the stages of the statistical method and articulates the probabilistic and statistical concepts used.

Keywords: Competence-based teaching, Probability, Statistics, Statistical Inference, Engineering.

 

Recibido: 24/04/2023 - Aceptado: 28/07/2023

 

1. INTRODUCCIÓN

Entre los acuerdos establecidos por la Asociación Iberoamericana de Instituciones de Enseñanza de la Ingeniería (ASIBEI) y el Consejo Federal de Decanos de Ingeniería (CONFEDI) de Argentina, se encuentra la elección de un modelo educativo que marca un cambio de perspectiva al considerar una Enseñanza por Competencias (CONFEDI, 2016).

Las competencias apuntan a capacidades complejas e integradas que incorporan la ética y los valores, están relacionadas con distintos tipos de saberes (teórico, contextual y procedimental), dependen del saber hacer y están expresadas en términos del contexto profesional del ingeniero (CONFEDI, 2018).

Los acuerdos entre ASIBEI y CONFEDI comenzaron hace más de 25 años, y coinciden con la propuesta del Massachusetts Institute of Technology junto con tres universidades de Suecia: Chalmers Institute of Technology, Linköping University y Royal Institute of Technology, quienes, en el año 2000, crean el proyecto llamado iniciativa CDIO, por su sigla en español, estableciendo que la ingeniería consiste en Concebir, Diseñar, Implementar y Operar (Restrepo y Lopera, 2015).

Este proyecto desafía articular las ciencias básicas con las ciencias de la ingeniería, al orientar una Enseñanza por Competencias. En este desafío se incluye vincular la Estadística, como una de las ciencias básicas, con las asignaturas propias en la formación del ingeniero. Sin embargo, esta asignatura es considerada “difícil” para los estudiantes de ingeniería (Alvarado y Batanero, 2007) y, tal como señalan Alvarado et al. (2018), los planes de estudio actuales no promueven la comprensión profunda de conceptos básicos. Estos autores señalan que se descuida la importancia de apropiarse de conceptos y procedimientos previos a la Inferencia Estadística, tales como el análisis de gráficos, las medidas de tendencia central y de dispersión.

La Facultad de Ingeniería de la Universidad Nacional de Mar del Plata, Argentina, considera en sus nuevos planes de estudio, la propuesta del CONFEDI (2018) con sus estándares de segunda generación para la Acreditación de Carreras de Ingeniería en la República Argentina. En ese marco, los responsables de la asignatura Estadística Básica, seleccionaron contenidos mínimos sobre los que definieron los resultados de aprendizaje, entendidos como las competencias de Estadística Básica, con la intención de aplicar el proceso de Concebir- Diseñar- Implementar- Operar, implícito en ellos.

Dos de los resultados de aprendizaje (RA3 y RA5) formulados para la asignatura, involucran habilidades integradas y proporcionan el contexto para el desarrollo de la temática de este trabajo. Ambos resultados de aprendizaje se vinculan con la estadística descriptiva, la teoría de probabilidades y la Inferencia Estadística. Están expresados con el formato [verbo] + [contenido] + [condición] + [finalidad] (Kowalski, et al., 2016), donde puede observarse la cantidad de conceptos involucrados y las habilidades requeridas cuando se trata de aprender Inferencia Estadística en carreras de ingeniería:

RA3: [Analiza e interpreta] [la distribución de datos] [para la resolución de problemas reales o simulados de la ingeniería], [mediante la identificación del experimento aleatorio asociado a la variable estadística discreta o continua del problema y a la caracterización de su modelo probabilístico respectivo, aplicando sus propiedades y sus características numéricas].

RA5: [Resuelve] [problemas de la ingeniería relativos a la inferencia] [a partir de la información obtenida de la muestra, del tamaño de la misma, de la confiabilidad pretendida, diferenciando en los casos necesarios si la varianza poblacional es o no es conocida, utilizando aplicaciones informáticas y las distribuciones muestrales respectivas de cada estadístico] [para la estimación de parámetros y la aplicación de pruebas de hipótesis].

Para desarrollar estas habilidades, es necesario que el estudiante esté familiarizado con conceptos como los de población y muestra, parámetro y estadístico, variable estadística y su variable aleatoria asociada, distribución empírica y distribución muestral del estadístico, estimador y estimación, valor observado y valor crítico en las pruebas de hipótesis, entre los más importantes.

Lo cierto es que, al llegar a la unidad correspondiente a Inferencia Estadística, los estudiantes aplican estos conceptos sin comprenderlos en su totalidad. Estos conceptos debieran ser trabajados previamente, en forma paralela, para ser comparados antes y después de la experimentación y para la verificación de la ley de los grandes números (Figueroa, 2017). En general, en los libros de texto de Probabilidades y Estadística se los presenta desvinculados entre sí: la teoría de probabilidades, por un lado, con sus distribuciones teóricas de probabilidad, y la estadística descriptiva, por el otro. Al llegar a la inferencia, que es el momento en que se trabaja simultáneamente con la probabilidad y la estadística, el estudiante “olvida” o no relaciona lo aprendido anteriormente con los conceptos relativos a estimación o pruebas de hipótesis, por lo que no puede justificar procedimientos.

Ruiz y Albert (2013) muestran las dificultades en el aprendizaje del concepto probabilístico de variable aleatoria y destacan la importancia de su vinculación con la variable estadística, ya que es el fundamento para el estudio de la Inferencia Estadística.

El trabajo de Meyer et al. (2008) plantea el análisis de contenido de ideas estadísticas fundamentales para la enseñanza y aprendizaje de la Inferencia Estadística Paramétrica (IEP). Si bien se restringe a las carreras de las Ciencias Sociales, dichas ideas fundamentales coinciden a las establecidas en este trabajo, implementadas en un curso introductorio de Estadística para ingenieros: Variabilidad, Frecuencias Empíricas y Frecuencias Teóricas, Población Estadística, Muestra al Azar, Incertidumbre vs. Determinismo, Técnicas Empíricas vs. Métodos Matemáticos. Los autores también reafirman el concepto de la naturaleza de la Inferencia Estadística, dada por diferenciar el “conocer” del “saber hacer” y/o del “saber cómo hacer”, lo cual coincide con la competencia implícita citada en los resultados de aprendizaje mencionados anteriormente. Por lo tanto, las ideas desarrolladas en este trabajo están en consonancia con estos autores, en el sentido de que resulta imprescindible el diseño y la construcción de procesos de enseñanza y aprendizaje que consideren la Inferencia Estadística como metodología, ya que es una característica intrínseca de la Estadística.

Siguiendo esa línea de investigación, Makar y Rubin (2009, citado en Sánchez y Ruiz, 2017) definen la inferencia informal como un proceso para aprender estadística, que incluye generalizar y/o predecir al observar más allá de los datos, usar los datos como evidencia y utilizar un lenguaje probabilístico al describir generalizaciones, incluyendo ideas informales con cierto grado de certeza, a partir de las conclusiones propuestas. Según estos autores, el eje del razonamiento inferencial informal consiste en profundizar la comprensión de los estudiantes sobre el objetivo propuesto, la interpretación y el análisis de los datos para elaborar conclusiones en relación al contexto. Utilizan la palabra informal como una aplicación del razonamiento inferencial fuera de los procedimientos formales.

Sánchez y Ruiz (2017) señalan que, aunque no se cuente con una definición formal de la Inferencia Informal, la idea que subyace en las conceptualizaciones de investigadores, es la misma: se elige reflexionar sobre ideas informales para efectuar conclusiones utilizando argumentos que consideran la variabilidad, el análisis que va más allá de datos y la evidencia que muestran los datos.

Los profesores deben partir de la base de considerar que los datos no están sujetos a fenómenos deterministas, sino que están sujetos a la variabilidad, tamaño de la muestra y formas de representación, por lo que estos elementos deben ser integrados de forma conjunta y no trabajarse aisladamente. (Sánchez y Ruiz, 2017, p. 128)

En la inferencia informal, entendida como un proceso para aprender estadística, se comparan distribuciones empíricas de muestras aleatorias de distintos tamaños, seleccionadas de una población dada mediante la simulación. Se analiza la variabilidad y simetría de las distribuciones empíricas en forma gráfica y analítica, y se resumen los datos en los casos posibles, calculando medidas descriptivas.

En consecuencia, este artículo tiene como objetivo presentar y fundamentar una propuesta didáctica que, en una primera etapa, utiliza los recursos de la inferencia estadística informal a través de actividades que vinculan la teoría de probabilidades con la Estadística para la comprensión de las ideas fundamentales de la estadística y, en una segunda etapa, se aplican técnicas de estimación y de pruebas de hipótesis para contrastar las conclusiones obtenidas previamente.

De esta forma, la propuesta considera la Inferencia Estadística como metodología, en términos de Meyer (2005), y con sentido estadístico, siguiendo las recomendaciones de Batanero (2013a).

 

2. ANTECEDENTES

 

Meyer (2005) analiza los libros de texto para la formación en Inferencia Estadística, destinados a estudiantes del área de Educación, Humanidades y Ciencias Sociales. Destaca que, en ellos, los conceptos disciplinares se encuentran reducidos a la lógica matemática interna de los métodos y su cálculo e interpretación es parcial, sin las características epistemológicas y el análisis del valor de verdad del conocimiento, que se adquiere mediante razonamientos inferenciales en situaciones de incertidumbre. El autor señala que las dificultades podrían reducirse si se considerara el significado de la Inferencia Estadística como un proceso metodológico, vinculado a la producción de conocimiento experimental. En este escenario, Meyer afirma que los formadores, provenientes de distintos campos del saber, poseen conocimientos parciales del proceso de Inferencia Estadística, relacionados principalmente con el cálculo estadístico. Esto puede verificarse en el proceso de aprendizaje en niveles de pregrado y grado porque se accede relativamente fácil al cálculo estadístico y con mucha dificultad a la práctica experimental de las ideas estadísticas fundamentales.

Por su parte, Retamal (2013) establece que las distribuciones muestrales son un tema difícil para los estudiantes por la cantidad de conceptos asociados, los tipos de lenguaje y representaciones, propiedades, procedimientos y argumentos utilizados. Considera que, en el currículo de ingeniería, la estadística puede pensarse como una etapa de transición entre los conocimientos matemáticos y los de ingeniería. Especifica que las distribuciones muestrales son importantes en el trabajo del ingeniero al brindar herramientas metodológicas para el análisis de la variabilidad, determinar relaciones entre variables, mejorar las predicciones y la toma de decisiones en condiciones de incertidumbre.

Chance et al. (2004, citado en Retamal, 2013), reconocen a la distribución muestral como la piedra angular de la Inferencia Estadística. Pfannkuh y Wild (2004, citado en Retamal, 2013), señalan que, para la comprensión de las distribuciones muestrales, un prerrequisito esencial es apropiarse de la idea de distribución y variabilidad, ya que esos conceptos surgen naturalmente en el análisis de datos, previo a los conceptos de inferencia.

En la misma línea de investigación, Inzunza (2017) se refiere a las distribuciones muestrales como un concepto fundamental, en el cual se basan los métodos de Inferencia Estadística. Señala que el enfoque de su enseñanza ha sido hasta ahora formal deductivo, que requiere una adecuada comprensión de conceptos de estadística y probabilidad como población, parámetro, estadístico, muestreo aleatorio, variables aleatorias y distribuciones de probabilidad. Destaca también que el lenguaje matemático utilizado está fuera del alcance de muchos estudiantes y plantea que, desde esta perspectiva, si bien los estudiantes aplican fórmulas y procedimientos para resolver un problema, no siempre logran comprender el proceso y los conceptos que subyacen en una inferencia.

Una de las maneras de abordar esta problemática, es a través de la utilización de ambientes computacionales. Al respecto, Alvarado et al. (2013) realizan una descripción de investigaciones sobre la comprensión de distribuciones muestrales con el uso de recursos informáticos.

• Inzunza (2007) y Chance et al. (2007), citados en Alvarado et al. (2013), sugieren el uso de applets disponibles en la web, por el apoyo que aportan los recursos informáticos en la simulación de fenómenos aleatorios para la visualización de conceptos abstractos, exploración de datos, representaciones gráficas de distribuciones, entre las actividades más destacadas.

• Batanero et al. (2001, citado en Alvarado et al., 2013), describen una experiencia de enseñanza de la distribución normal dentro de un curso de análisis de datos, con estudiantes universitarios en un ambiente computacional. Si bien utilizaron el software y adquirieron muchos de los elementos de significado considerados en la enseñanza, se observaron dificultades en la comparación de las distribuciones empíricas y teóricas, en interpretar ciertos gráficos y resúmenes estadísticos, así como un insuficiente análisis y síntesis.

• Del Mas et al. (2004, citado en Alvarado et al., 2013), también utilizan simulaciones en su enseñanza y destacan las dificultades en la comprensión del efecto del tamaño de la muestra sobre la variabilidad de la distribución muestral y la confusión entre el parámetro y el estadístico respectivo. Sugieren que la tecnología no es suficiente para la comprensión y consideran dar un rol a la enseñanza de tipo constructivista.

• Inzunza (2006, citado en Alvarado et al., 2013), utiliza simulaciones para analizar el significado de las distribuciones muestrales mediante el software Fathom. Señala errores frecuentes de los estudiantes en el uso de representaciones numéricas, con un manejo superficial de conceptos y de propiedades de las distribuciones muestrales, con escasa argumentación.

• Retamal et al. (2007, citado en Alvarado et al., 2013), realizan una enseñanza contextualizada de las distribuciones muestrales, con el programa @risk, en estudiantes de ingeniería. Sugieren desarrollar las representaciones gráficas y algebraicas en simulaciones, según el tipo de variable aleatoria.

• Ramírez (2008, citado en Alvarado et al., 2013), estudia los tipos de razonamiento que muestran estudiantes de maestría, utilizando el software Fathom para la simulación de un desarrollo empírico de la distribución normal, utilizando un enfoque frecuencial. Si bien el recurso contribuyó a modificar conceptos erróneos sobre esta distribución, se debe focalizar la atención en el lenguaje, la simbología utilizada por los estudiantes y el uso de datos reales.

• Olivo y Batanero (2007, citado en Alvarado et al., 2013), señalan el significado que tiene un intervalo de confianza como procedimiento y destacan la necesidad de adquirir elementos previos, como el de la distribución muestral, para la comprensión del concepto de intervalo de confianza. Los errores observados en los estudiantes hacen recomendar a los autores el diseño de secuencias didácticas con simulaciones para aumentar la relevancia del aprendizaje.

Estas investigaciones tienen elementos comunes para el abordaje de la enseñanza de las distribuciones muestrales: contar con un recurso informático que permita simular un experimento aleatorio y así visualizar las distribuciones empíricas obtenidas. Si bien este recurso contribuye a una enseñanza contextualizada de la estadística, siguen apareciendo errores de los estudiantes referidos a la comprensión superficial de conceptos relativos a la inferencia, a la simbología utilizada y a la confusión entre distribuciones experimentales y teóricas, entre otros.

Asimismo, la investigación de Terán y Ciminari (2019) describe errores cometidos por los estudiantes en la resolución de situaciones problemáticas, en temas de Inferencia Estadística, entre los cuales se encuentran:

• Planteo incorrecto de las hipótesis nula y alternativa: se observaron casos donde invierten las hipótesis, casos donde utilizan el estadístico en lugar del parámetro, y otros, donde no plantean las hipótesis.

• Confusión entre parámetro y estadístico: se incluyeron casos donde toman en forma equivocada los datos de los parámetros y de los estadísticos, no pudiendo distinguir cada uno.

• Elección y/o escritura incorrecta del estadístico de prueba: eligen de manera incorrecta el estadístico de prueba a considerar, o bien, lo eligen de manera correcta, pero hay algún error dentro de la fórmula del mismo.

• Búsqueda errónea del valor de tabla: buscan el valor en la tabla correcta, pero de manera errónea, o utilizan una tabla que no corresponde.

• Error en la elección de la distribución de probabilidad: eligen de manera incorrecta la distribución de probabilidad del estadístico, o bien, la eligen correctamente, pero no escriben de manera correcta sus parámetros y grados de libertad correspondientes.

• Interpretación errónea en términos de la situación problemática: se observa que el desarrollo del test de hipótesis se aplica en forma correcta, pero al concluir en términos de problema, no interpretan coherentemente de acuerdo a la situación planteada.

 

3. FUNDAMENTOS PARA LA PROPUESTA DIDÁCTICA

 

Si se revisan los textos de estadística para carreras de ingeniería, se observa que, en general, comienzan con estadística descriptiva y definen el concepto de variable estadística como aquella característica medible que es estudiada a partir de los resultados obtenidos de una muestra. Llegado el capítulo de la teoría de probabilidades, se suele presentar el concepto de variable aleatoria sin establecer ninguna vinculación explícita con la variable estadística.

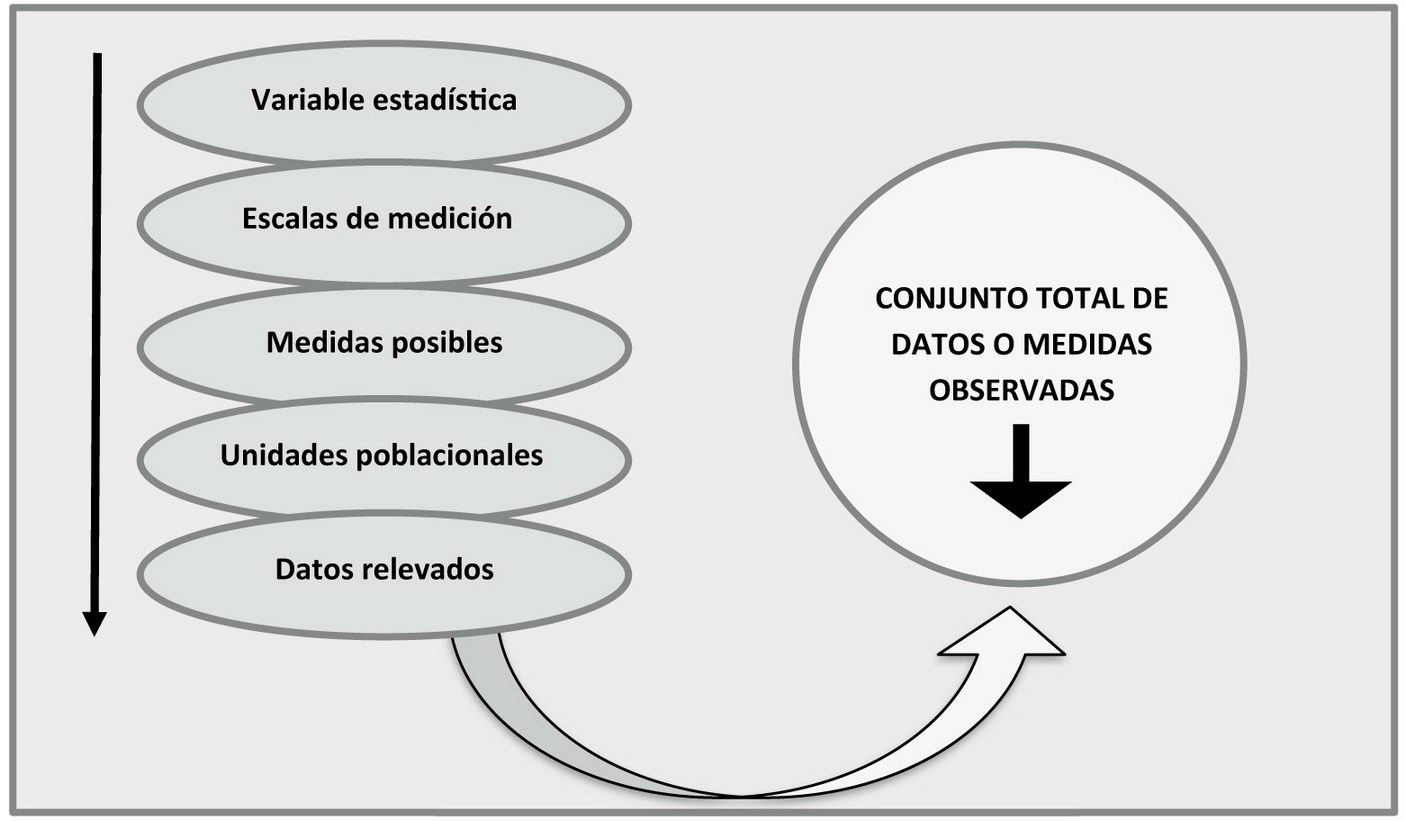
La propuesta didáctica que se presenta en este trabajo, considera que el puente que une la Estadística y la Probabilidad está dado por la conexión entre estos objetos matemáticos: variable aleatoria y variable estadística, a su vez, de la variable estadística surgen los conceptos previos necesarios para llegar al de población estadística, representados en la Figura1.

Determinar el experimento aleatorio asociado a estas variables y cuándo se realiza el mismo, distingue dos momentos: un antes y un después. Esta mirada es esencial para relacionar e identificar estas variables.

Por un lado, se comienza por identificar el contexto en el que se está trabajando: en el antes de la experimentación, el contexto es poblacional. Esto significa considerar el conjunto de todos los resultados posibles de dicho experimento aleatorio, lo que da lugar a asignar un valor numérico o un intervalo a cada uno de estos resultados. De esta manera, se determina el recorrido de la variable aleatoria con su distribución de probabilidades correspondiente, obtenidas con el cálculo que proporciona la teoría de probabilidades.

Por otro lado, en el después del experimento, a menos que se realice un censo, el contexto en el que se trabaja es muestral. La toma de datos se obtuvo de una muestra con datos reales o simulados. Los datos, es decir, los valores obtenidos en la muestra, no necesariamente son todos los posibles (eso depende del tamaño de la muestra y de la muestra seleccionada), pero son los valores que tomó la variable estadística. Su distribución de frecuencias relativas es su distribución empírica o experimental.

Una vez identificados el escenario poblacional y muestral, con sus variables respectivas, las distribuciones de probabilidades (distribuciones teóricas) no debieran confundirse con las distribuciones frecuenciales (distribuciones empíricas).

Llegado este punto, y sabiendo que en Inferencia Estadística se utiliza el concepto de población, como la variable aleatoria de estudio con su correspondiente distribución de probabilidades –pero también como el conjunto total de datos–, es necesario destacar la idea común que subyace en ellas y vincularlas.

En las primeras actividades de esta propuesta, se estudia el caso de una población cuya distribución es de Bernoulli. La proporción de éxitos observada en una muestra grande de ella, se acerca a la proporción real de éxitos en la población de Bernoulli. De esta manera, se verifica el Teorema de la ley de los grandes números, que establece que, a medida que el tamaño de la muestra aumenta, la media muestral se acerca a la media poblacional. Análogamente, se analiza el caso de una población binomial: se seleccionan muestras de esa población y se verifica la ley de los grandes números. Se trabaja en clase, comparando estimaciones de los parámetros obtenidos en muestras de distintos tamaños para conjeturar acerca de los parámetros poblacionales respectivos.

Para estudiar las distribuciones de los estadísticos muestrales, por ejemplo, el de la proporción muestral, los estudiantes parten de la definición de la media aritmética, y verifican que la proporción de éxitos de la muestra de una población de Bernoulli, es la media muestral. Se plantean actividades referidas a seleccionar muestras aleatorias de la población de Bernoulli y representar gráficamente sus distribuciones de frecuencias relativas. De la misma forma, se trabaja con una población binomial. Posteriormente, se estudian los casos para una buena aproximación de la distribución binomial a la distribución normal y la aplicación de la corrección por continuidad.

Desde la teoría de probabilidades, se define la proporción muestral como la suma de una gran cantidad variables independientes de Bernoulli dividida por una constante n. Luego, a través de actividades en clase, los estudiantes verifican que, al aplicar el Teorema del Límite Central, la proporción muestral se distribuye normalmente. Deducen también la esperanza y varianza de la proporción muestral, a partir de la esperanza y varianza de la variable binomial. Siguiendo en el contexto de las probabilidades, una vez que los estudiantes deducen las distribuciones de los estadísticos p̂ y x̅ y calculan su esperanza y varianza para muestras grandes, están en condiciones de avanzar con las técnicas de estimación y/o pruebas de hipótesis para los parámetros respectivos P y µ de estos estadísticos o estimadores.

En resumen, esta propuesta didáctica aplica la inferencia informal integrando ambientes computacionales, a través de simulaciones para partir del análisis de datos a la inferencia, en términos de Batanero (2013b). Pretende esclarecer la confusión entre parámetro y estadístico, diferenciar las distribuciones empíricas de las teóricas y darle sentido a la comparación entre el valor crítico y el observado, para la toma posterior de decisiones en la resolución de problemas de inferencia en ingeniería. De esta forma, se establece una correspondencia entre los conceptos seleccionados en los contextos probabilístico y estadístico.

La propuesta utiliza el concepto de “practica matemática” que proporciona el Enfoque Ontosemiótico del Conocimiento y la Instrucción Matemáticos (EOS). Entre sus características, este modelo didáctico destaca la articulación de los aspectos institucionales y personales del conocimiento matemático, la asignación de un papel clave a la actividad de resolución de problemas socialmente compartida, a los recursos expresivos y a la coherencia entre supuestos pragmatistas y referenciales sobre el significado de los objetos matemáticos. Considera práctica matemática “a toda actuación o expresión (verbal, gráfica, etc.) realizada por alguien para resolver problemas matemáticos, comunicar a otros la solución obtenida, validarla o generalizarla a otros contextos y problemas” (Godino y Batanero, 1994, p. 334).

Santarrone y Meyer (2020) proponen un enfoque para favorecer el aprendizaje de las ideas fundamentales de la Inferencia Estadística paramétrica, en alumnos de la Facultad de Ciencias Económicas de la UNL. Su trabajo muestra una secuencia de conceptos previos al presentar el concepto de población estadística.

 

Figura 1

Secuencia de conceptos previos al presentar el concepto de población estadística (Meyer, 2005)

 

Tabla 1

Prácticas matemáticas requeridas al estudiante en el proceso de vinculación entre conceptos probabilísticos y conceptos estadísticos para el diseño de las actividades.

ANTES del experimento aleatorio Teoría de Probabilidades	Grupo de Prácticas Matemáticas requeridas al estudiante en el proceso de vinculación	DESPUÉS del experimento aleatorio Estadística
Espacio Muestral	1. Identificar el experimento aleatorio asociado al problema presentado.	Suceso o Evento
Variable aleatoria Distribución de probabilidades de una variable aleatoria. (Distribución Teórica)	2. Vincular la variable estadística y su variable aleatoria asociada a través de: • Calcular probabilidades de variables aleatorias discretas. • Simular mediante un software, datos reales como los valores que toma una variable estadística. • Construir tablas y representaciones gráficas con datos simulados y con probabilidades calculadas. • Observar más allá de los datos y usar los mismos como evidencia. • Generalizar y/o predecir observaciones a partir de los datos obtenidos. • Utilizar un lenguaje probabilístico al describir generalizaciones. • Proponer conjeturas o ideas informales con cierto grado de certeza a partir de las conclusiones propuestas. • Comparar distribuciones empíricas, con distribuciones teóricas, reconociendo que las empíricas pueden tomar sólo algunos valores de la variable aleatoria, mientras que las distribuciones teóricas toman todos los valores posibles de la variable aleatoria. • Verificar la ley de los grandes números.	Variable Estadística Distribución de frecuencias relativas de una variable estadística. (Distribución empírica)
Población Dada por todos los valores que toma una variable aleatoria con su respectiva distribución de probabilidades.	3. Establecer esta secuencia de conceptos previos para arribar al concepto de población estadística: • Plantear preguntas para caracterizar la población que permiten resolver un problema dado. • Definir la variable estadística involucrada. • Medir esa variable según su escala de medición. • Decidir cuáles son las unidades poblacionales de interés que caracterizan a la población y las otras variables estadísticas involucradas.	Población estadística Dada por las unidades elementales que forma el conjunto total de datos relevados o medidas observadas.
Muestra aleatoria de tamaño n Conjunto de n variables aleatorias independientes e idénticamente distribuidas extraídas de la población.	4.a. Seleccionar muestras aleatorias extraídas de poblaciones dadas para conocer una característica medible de dicha población. • Identificar a cada observación como el resultado de la medición de una característica medible de la población real o simulada. • Establecer la correspondencia entre cada variable aleatoria y la medida observada obtenida en el muestreo.	Muestra aleatoria de tamaño n n observaciones de la población elegidas aleatoriamente
Parámetro Es una característica medible de la población. Es un valor constante que define una población. Suelen notarse con letras griegas. A menos que se realice un censo, son desconocidos.	4.b. • Comparar medidas descriptivas poblacionales y muestrales. • Verificar la ley de los grandes números calculando medias de muestras de distintos tamaños para compararlas con la media poblacional en una población de Bernoulli. • Verificar la ley de los grandes números calculando las medias de muestras de distintos tamaños para compararlas con la media poblacional en una población binomial.	Estadístico/a Es una característica medible en la muestra. Es un valor calculado con los datos de una muestra. Estima, en forma puntual, a los parámetros de una población.
Estadístico o Estimador Es una variable aleatoria (por ser cualquier operación aritmética que se realiza con las variables de una muestra aleatoria). La distribución de probabilidades del estadístico o estimador está dada por todos los resultados obtenidos de ese estadístico en cada una de las muestras posibles de tamaño n extraídas de la población.	4.c. • Construir distribuciones empíricas de la media y de la proporción muestrales a partir de selecciones aleatorias de muestras del mismo tamaño. • Construir la distribución de la varianza muestral. • Comparar distribuciones muestrales empíricas con distribuciones muestrales teóricas. • Verificar de la ley de los grandes números. 5.a. Resolver problemas aplicando estimaciones donde se identifican: • Parámetro y estadístico. • Distribución del estimador del parámetro en cuestión. • Error de muestreo y confiabilidad. • Esperanza y varianza del estadístico seleccionado. • Estimador y estimación. • Valor crítico y valor observado.	Estimación puntual: Es el valor numérico del estadístico. Por intervalo: Con él se espera encontrar, con cierta confiabilidad, extremos que contengan al parámetro a estimar. Los extremos dependen de la muestra, del tamaño de la misma y del riesgo aceptado en la estimación.
Valor crítico Es un punto en la distribución de probabilidades del estadístico que divide al recorrido de la variable en subconjuntos con áreas o probabilidades que permiten la toma de decisiones a partir del valor observado.	5.b. Resolver problemas aplicando pruebas de hipótesis, donde se identifican: • Parámetro y estadístico. • Distribución del estimador del parámetro en cuestión. • Error de muestreo y confiabilidad. • Esperanza y varianza del estadístico seleccionado. • Hipótesis nula y alternativa. • Nivel de significación. • Estimador y estimación. • Valor crítico y valor observado.	Valor observado Es un valor calculado con los datos de una muestra. Es un valor posible en la distribución de probabilidades del estadístico correspondiente. Se estandariza para poder ser comparado con el valor crítico.

 

4. ACTIVIDADES SELECCIONADAS Y FUNDAMENTADAS PARA LA PROPUESTA

 

En las siguientes subsecciones se describen la fundamentación y los enunciados de posibles actividades que se pueden realizar, considerando las prácticas matemáticas agrupadas de 1 a 5 en la Tabla1, de acuerdo a los conceptos probabilísticos y estadísticos trabajados.

 

4.1. Identificar del experimento aleatorio asociado al problema presentado

 

4.1.1. Fundamentación de la Actividad 1

Para la introducción de las distribuciones de probabilidad discretas, se pensó en seleccionar un problema que pueda modelizarse con la distribución de Bernoulli primero, y binomial después. El objetivo es interpretar la variable binomial como el número de éxitos obtenidos en n pruebas repetidas de Bernoulli y aplicar el razonamiento estadístico en términos de Wild y Pfannkuch (1999), más específicamente, aplicar los modos fundamentales de razonamiento estadístico (reconocer la necesidad de los datos, la transnumeración. la percepción de la variación, el razonamiento con modelos estadísticos y la integración de la estadística y el contexto).

 

4.1.2. Enunciado de la Actividad 1 para trabajar en grupos

En el contexto de las telecomunicaciones, cualquier señal debe considerarse aleatoria, ya que, por muchas razones, no existen garantías de que la señal enviada sea exactamente igual a la señal recibida.

1. ¿Cuál/es podría/n ser el/los experimento/s aleatorio/s considerados?

2. Elegir un solo experimento aleatorio y determinar sus resultados posibles.

3. Se transmite una sola señal y se observa si se recibe erróneamente. La probabilidad de que se reciba de manera errónea es p=0.4. Escriban la distribución de probabilidades de la variable aleatoria asociada a este experimento en una tabla de valores.

4. Una variable es de Bernoulli, si toma dos valores posibles: X1 = 1 Es el éxito (resultado esperado del experimento) con probabilidad de éxito “p” y X2 = 0 (Fracaso, resultado no esperado), con probabilidad 1-p. La variable asociada a este experimento en el punto 3. ¿Es una variable de Bernoulli? Justifiquen.

5. Se transmiten 3 señales y se observa el estado de su llegada. (1: erróneo; 0: correcto)

a) ¿Cuál es el espacio muestral asociado?

b) Se define la variable aleatoria X: “número de señales erróneas recibidas en las tres transmisiones” Determinen el conjunto de valores que toma la variable.

c) Analicen si las tres señales enviadas (las tres pruebas repetidas) son independientes.

d) ¿Son mutuamente excluyentes los sucesos (0, 1,1) y (1,1,0)? Justifiquen cada respuesta.

e) Calculen la probabilidad de que se reciban exactamente 2 señales erróneas recibidas en tres transmisiones.

f) Calculen la distribución de probabilidades de la variable X: “nº de señales erróneas recibidas en tres transmisiones”. Verifiquen con GeoGebra.

g) Representen gráficamente esta distribución de probabilidades. Verifiquen con GeoGebra.

 

4.2. Vincular la variable estadística y su variable aleatoria asociada a través de:

 

• Calcular probabilidades de variables aleatorias discretas.

• Simular, mediante un software, datos reales que representen los valores que toma una variable estadística.

• Construir tablas y representaciones gráficas con datos simulados y con probabilidades calculadas.

• Comparar distribuciones empíricas, reconociendo que pueden tomar sólo algunos valores, con distribuciones teóricas, que toman todos los valores de la variable.

• Verificar la ley de los grandes números.

 

4.2.1. Fundamentación de la Actividad 2

Se realizan simulaciones del experimento aleatorio para distintos tamaños de muestras. Se destaca que cada resultado del experimento aleatorio corresponde a un valor que tomó la variable estadística asociada al experimento aleatorio. Se utiliza el comando de GeoGebra BinomialAleatorio(n, p) para
n = 1 y p = 0,4. Se hace notar que si n=1, la variable binomial es de Bernoulli. Se pretende que los estudiantes interpreten la variable binomial como el número de éxitos obtenidos en n pruebas repetidas de Bernoulli, al contar los unos de la planilla de cálculo. Se señala que el tamaño n de la muestra corresponde a la cantidad de pruebas repetidas independientes. También se destaca que aumentar el tamaño de muestra, permite observar la variación de las distribuciones de frecuencias en las muestras de la variable estadística “Número de señales erróneas transmitidas en 10, 100 y 500 transmisiones” respectivamente.

También se hace observar que los valores muestrales de p obtenidos en las distintas distribuciones de frecuencias, pasan de 0,5 a 0,38 para n = 10 y 100 respectivamente.

Para vincular la variable estadística con su variable aleatoria asociada, se enfatizan los contextos muestral y poblacional respectivamente, al comparar la distribución de frecuencias de la variable estadística con la distribución de probabilidades de la variable aleatoria de Bernoulli asociada. Se justifica esta vinculación con la ley de los grandes números. Asimismo, se destaca que GeoGebra utiliza la distribución binomial para n = 1 como población de Bernoulli. Esto evidencia la necesidad de que el estudiante identifique el experimento aleatorio simulado: cada número “uno” de la planilla de cálculo de GeoGebra, representa un éxito (una señal errónea), al simular la emisión de la señal. En este caso, el tamaño n de la muestra representa el número de transmisiones efectuadas.

Pero, para relacionar la variable aleatoria binomial con su variable estadística “número de señales erróneas en 10 transmisiones”, cada resultado obtenido en la simulación, utilizando el comando BinomialAleatorio(10, 0,4) es un número (del 0 al 10) de la planilla de cálculo y representa el número de éxitos obtenidos en 10 pruebas repetidas e independientes, es decir, en 10 transmisiones. Es importante destacar que, en este caso, el tamaño n de la muestra representa el número de veces “n” que se efectúa el experimento de transmitir 10 señales. De esta manera, se pretende que los estudiantes diferencien el número de pruebas repetidas independientes de la distribución binomial (en este caso 10) con el número de veces que se simula el experimento aleatorio ya que, por abuso de notación, al tamaño de una muestra también se lo llama n.

 

4.2.2. Enunciado de la Actividad 2 para trabajar en grupos

1. Simular el experimento aleatorio de transmitir 10 señales con probabilidad 0,4 de éxito.

Para ello, utilizar la distribución de Bernoulli con el comando de GeoGebra BinomialAleatorio(n, p) para n = 1 y p = 0.4. (Notar que si n = 1, la variable binomial es de Bernoulli). Al arrastrar el mouse en la planilla de cálculo de A1 a A10, se genera una muestra de tamaño n = 10. Crear una lista y darle un nombre a la lista de datos brutos, por ejemplo: muestra1. Son los resultados obtenidos de la variable estadística “número de señales erróneas transmitidas en 10 transmisiones”.

2. Tabular los datos obtenidos con el comando Tabla Frecuencias (lista de datos brutos, factor de escala) para lista de datos brutos: muestra1, para factor de escala: 1.

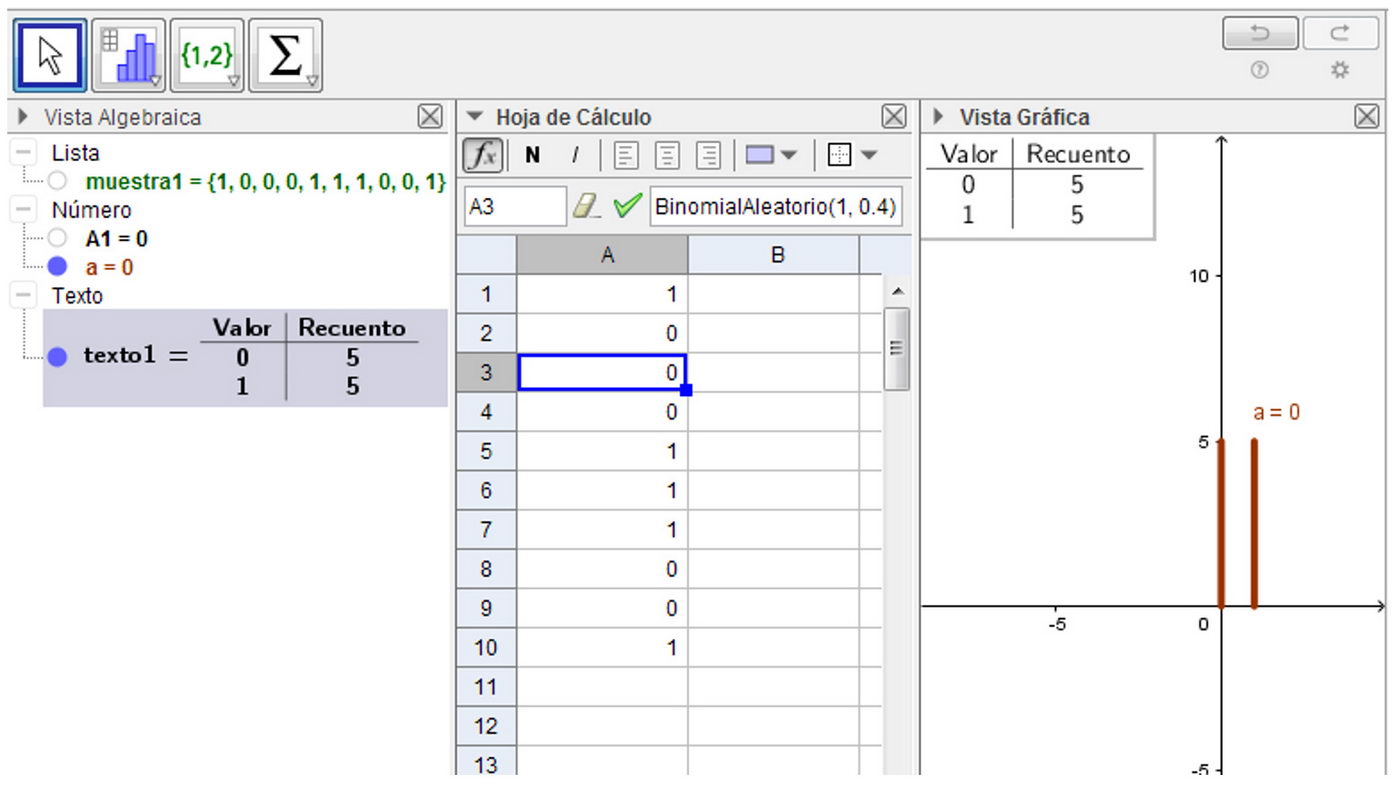
3. Graficar con el comando Barras(<Lista de datos brutos>, <Ancho de barras>, <Factor de escala vertical (opcional)>) para Lista de datos brutos: escribir “muestra1”, para Ancho de barras: 0 (para que sea un gráfico de bastones), para Factor de escala vertical (opcional): 1 (para trabajar con frecuencias absolutas). Para frecuencias relativas, el factor de escala es 1/n. En este caso, n=10. En la Figura 2 se resumen las resoluciones de los puntos 1, 2 y 3 de la Actividad 2 con frecuencias absolutas.

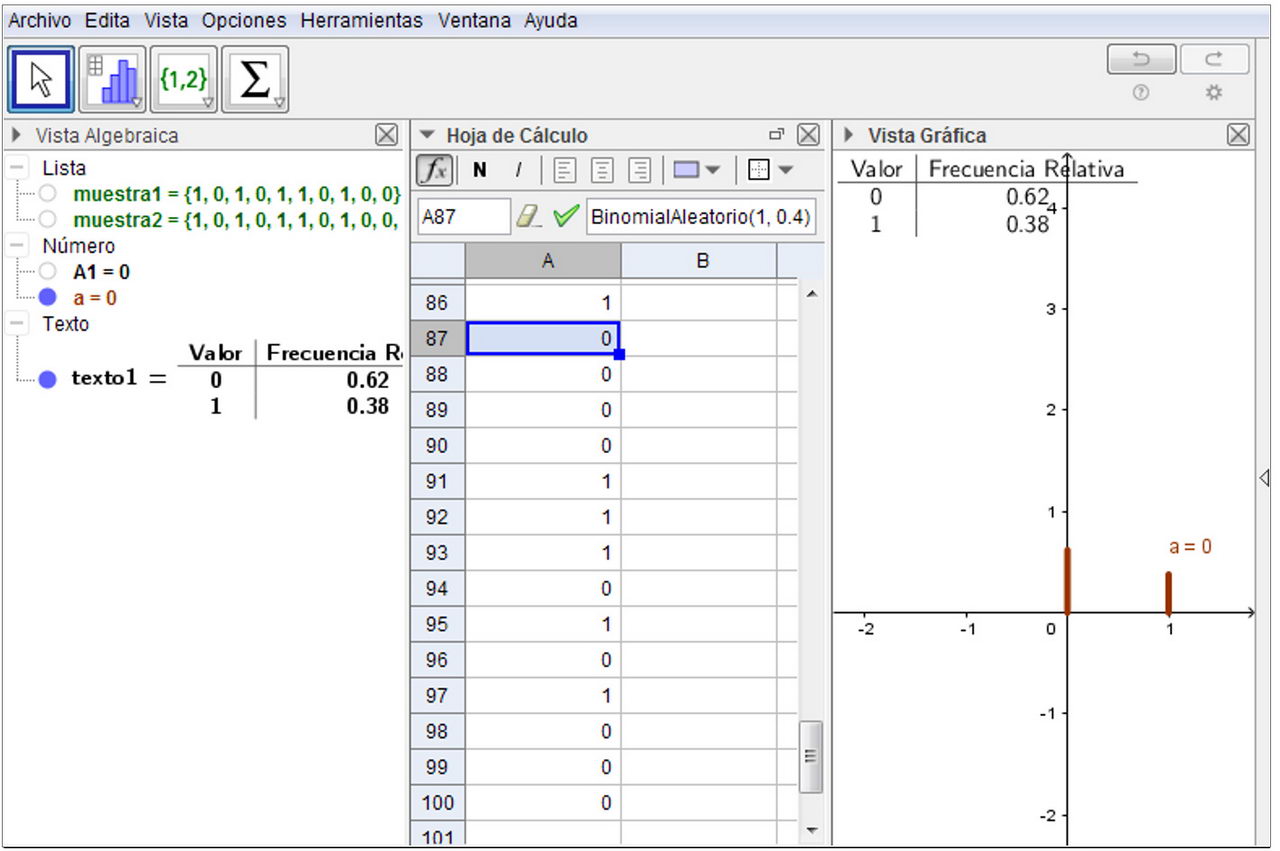
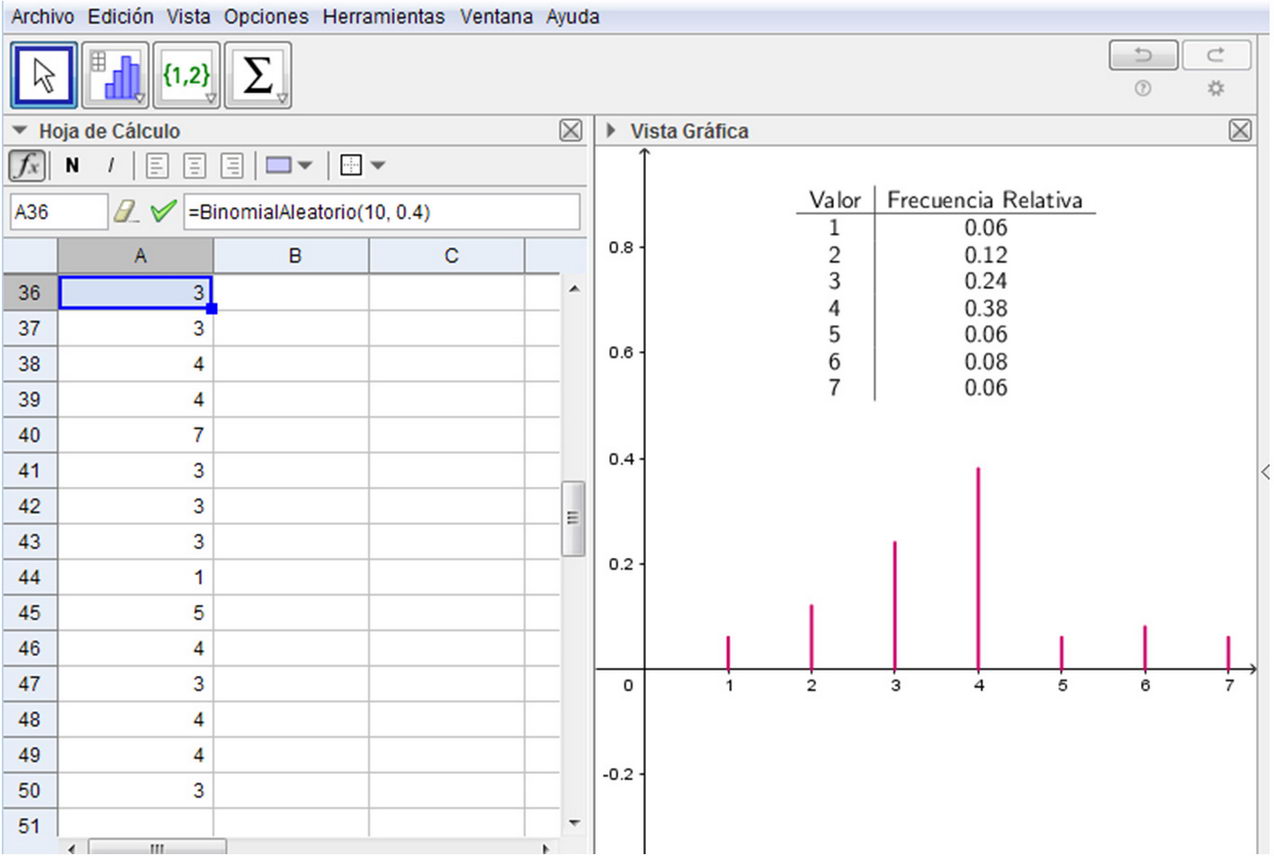
4. Simular el experimento aleatorio de transmitir 100 señales con probabilidad 0,4 tabular y graficar los datos simulados. Ídem para 500 señales. En la Figura 3 se muestra una simulación, efectuada con GeoGebra, de 100 transmisiones de señales.

5. ¿Se podría argumentar con herramientas teóricas que, cuanto mayor es el tamaño n de la muestra, más se acercan los valores muestrales de p (es decir, las frecuencias relativas) al valor teórico de probabilidad 0,4? Justifiquen.

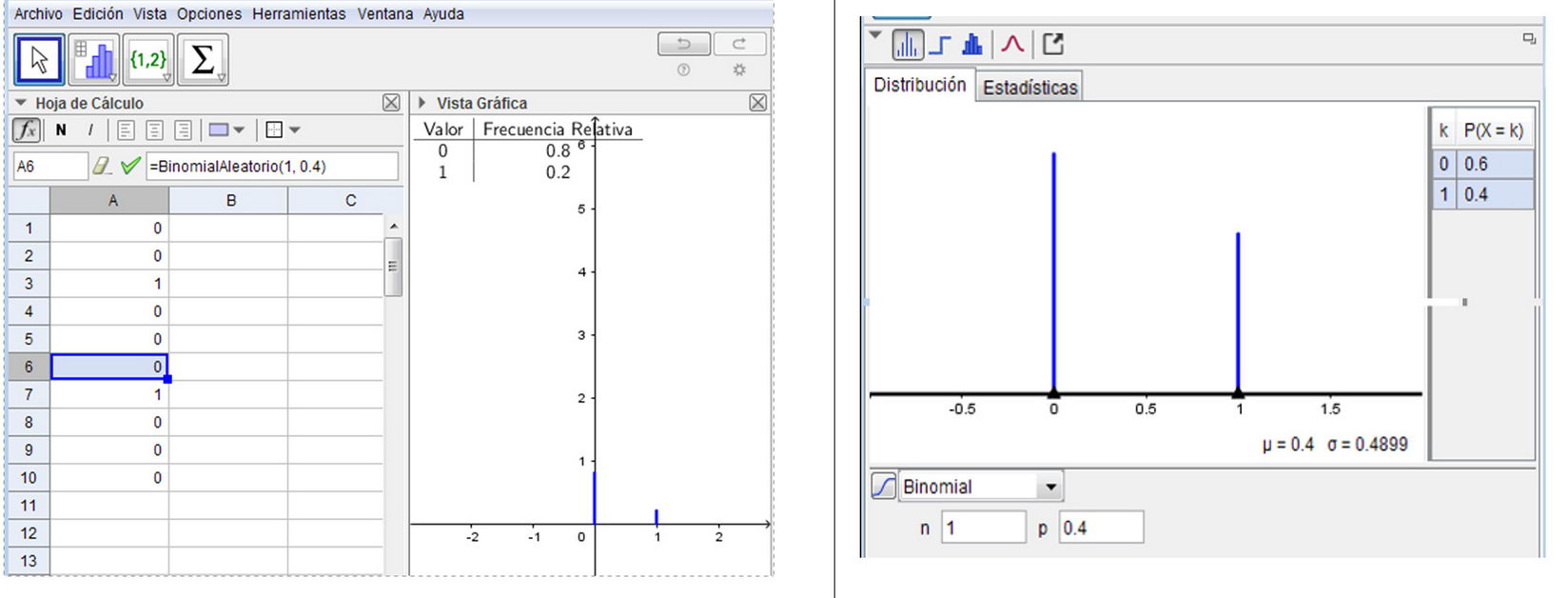
6. Comparar la distribución de frecuencias relativas de la variable estadística “Número de señales erróneas producidas en 10 transmisiones” con su variable aleatoria asociada. (Se espera obtener resultados como los que se muestran en la Figura 4).

 

Figura 2

Simulación de 10 transmisiones de señales en GeoGebra

 

Figura 3

Simulación de 100 transmisiones de señales en GeoGebra

 

Figura 4

Comparación de la distribución de frecuencias relativas de la variable estadística “Número de señales erróneas transmitidas en 10 transmisiones” con su variable aleatoria asociada: la Distribución Binomial para n=1 y p=0,4 (o de Bernoulli para p=0.4)

Variable estadística (Muestra)	Variable aleatoria (Población de Bernoulli)

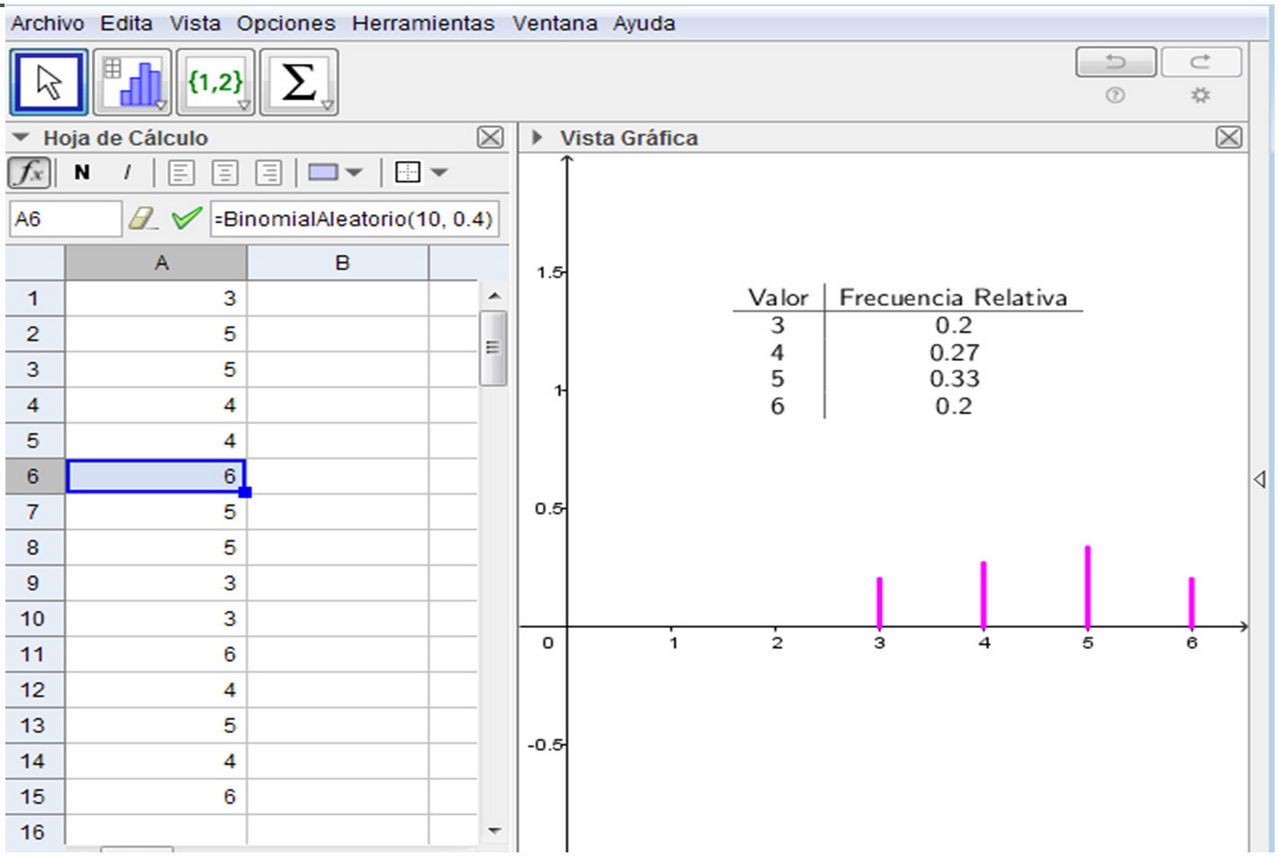
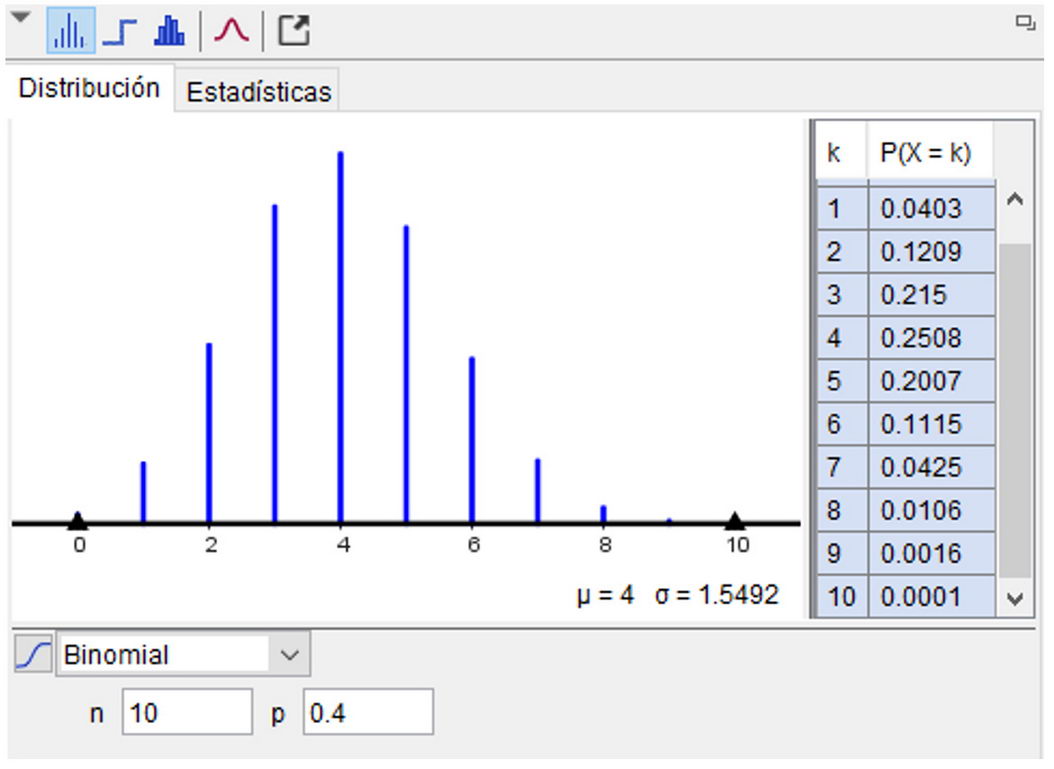
7. Comparar la distribución de frecuencias relativas de la variable estadística “Número de señales erróneas producidas en 10 transmisiones en una muestra de tamaño 15 y otra de tamaño 50” con su variable aleatoria asociada. (Se espera obtener resultados como los que se muestran en la Figura 5, donde los estudiantes verifican la ley de los grandes números al comparar las distribuciones de frecuencias relativas para los distintos tamaños de muestra, con la distribución de probabilidades dada en las tablas y en las representaciones gráficas.)

 

Figura 5

Distribución de frecuencias relativas de la variable estadística “Número de señales erróneas producidas en 10 transmisiones con p=0,4 en una muestra de tamaño 15 y otra de tamaño 50” y su variable aleatoria asociada.

Distribuciones empíricas o muestrales para n = 15 y para n = 50	Distribución teórica o población Binomial

 

4.3. Establecer una secuencia de conceptos previos para arribar al concepto de población estadística

 

Decidir cuáles son las unidades poblacionales de interés que caracterizan a la población y las otras variables estadísticas involucradas.

Plantear preguntas para caracterizar la población que permiten resolver un problema dado, definir la variable estadística involucrada, medir esa variable según su escala de medición, decidir cuáles son las unidades poblacionales de interés que caracterizan a la población junto a otras variables estadísticas involucradas.

 

4.3.1. Fundamentación de la Actividad 3

Caracterizar la población de estudio determina las unidades elementales que forma el conjunto total de datos relevados o medidas observadas. Establecer esta secuencia, es una práctica matemática que permite identificar cada observación como uno de los posibles valores que toma su variable aleatoria asociada. Vincula la población de la “teoría de probabilidades” con la población estadística.

 

4.3.2. Enunciado de la Actividad 3 para trabajar en grupos

Determinar el porcentaje de aprobados en el primer parcial de Estadística de la Facultad de Ingeniería de la Universidad Nacional de Mar del Plata de este año, en el turno tarde.

1) Se buscan preguntas que caracterizan a la población para resolver el problema:

¿Son estudiantes de ingeniería que cursan Estadística en este año? ¿Cuál universidad? ¿Qué turno? ¿Qué tipo de examen? ¿Cuál es el puntaje de aprobación?

2) Esas preguntas ayudan a definir la variable estadística: “estudiantes de Estadística de la Facultad de Ingeniería de la Universidad Nacional de Mar del Plata que aprobaron el primer parcial de la asignatura en este año”.

3) Se busca una forma de medir esta variable, según su escala de medición, para decidir cuáles son las unidades poblacionales de interés: estudiantes de Estadística de este año, de esta Facultad y Universidad que aprobaron el primer parcial de la asignatura obteniendo, al menos, 50 puntos.

De su observación, se definirá quiénes aprobaron y quienes no para determinar el porcentaje de aprobados en el primer parcial.

 

4.4. Seleccionar muestras aleatorias extraídas de poblaciones dadas para conocer una característica medible de dicha población

 

• Identificar a cada observación como el resultado de la medición de una característica medible de la población real o simulada.

• Establecer la correspondencia entre cada variable aleatoria y la medida observada, obtenida en el muestreo.

• Comparar medidas descriptivas poblacionales y muestrales.

• Representar gráficamente las distribuciones empíricas de la media y de la proporción muestrales, a partir de una selección aleatoria de muestras del mismo tamaño.

• Comparar distribuciones empíricas con distribuciones teóricas, para verificar la ley de los grandes números.

 

4.4.1. Fundamentación de la Actividad 4

Se comienza con la selección aleatoria de varias muestras extraídas de una población dada, ya sea con datos reales o simulados. El objetivo es estudiar el comportamiento de variables estadísticas, vincularlas con sus variables aleatorias asociadas y verificar resultados teóricos, considerando distintos tamaños de muestra y muestras del mismo tamaño para el estudio de los estadísticos muestrales.

Es importante señalar al estudiante que, si bien en la realidad cotidiana se selecciona una sola muestra representativa de la población y se trabaja con ella, el objetivo de la Inferencia Estadística paramétrica, es extraer conclusiones acerca de los parámetros desconocidos de la población, a partir de esa muestra. El alcance de los resultados dependerá si la selección de la muestra fue aleatoria, también dependerá de su tamaño y del error aceptado en la estimación o en la prueba de hipótesis.

La selección aleatoria de muestras del mismo tamaño permite el cálculo de los estadísticos de cada una y con ellos estudiar el comportamiento de sus distribuciones empíricas. La comparación posterior con las distribuciones muestrales respectivas, se establece al vincular la variable estadística con su variable aleatoria asociada.

Se propone una actividad integradora para que los estudiantes resuelvan una problemática, donde apliquen desde el análisis de datos hasta la inferencia, en un escenario de su profesión: en este caso se introduce la actividad a partir del estudio de pruebas mecánicas como el Ensayo de Tracción. Los ensayos de tracción, dentro de todas las pruebas mecánicas que se pueden realizar en un material, son esenciales y están estandarizados. Las propiedades mecánicas de los materiales indican el comportamiento de un material cuando se encuentra sometido a fuerzas exteriores, como un estiramiento del material por una fuerza externa a él. (Fuente: https://www.areatecnologia.com/materiales/ensayo-de-traccion.html).

Se proporcionan datos de cuatro poblaciones. Las dos primeras poblaciones, tienen una distribución asimétrica positiva y las dos últimas, se distribuyen normalmente. Se pretende que los estudiantes visualicen y comprueben que, aunque las dos primeras poblaciones son asimétricas, la distribución de sus medias muestrales respectivas en cada caso se distribuye normalmente para muestras de tamaño 30 como mínimo. Los estudiantes buscan argumentaciones para justificar este resultado. Se espera que apliquen el teorema central del límite. Las poblaciones 3 y 4 distribuidas normalmente, son utilizadas para los problemas de estimación y de pruebas de hipótesis, que requieren este supuesto de normalidad.

 

4.4.2. Enunciado de la Actividad 4 para trabajar en grupos

Los datos utilizados para esta actividad son datos reales suministrados por cuatro Laboratorios: 1,2,3 y 4. Describen la tensión de rotura de 100 probetas de un determinado polímero. Cada columna del fichero rotura.xls representa la tensión de rotura, según las mediciones efectuadas por cada laboratorio. Los análisis fueron solicitados por una empresa dedicada a la fabricación de soportes para GPS, para interiores de automóviles.

Cada grupo, de cuatro estudiantes, deberá descargar sus datos de un enlace dado.

1. Suponer que durante 20 días se realizaron 5 mediciones diarias acerca de la tensión de rotura de las probetas del Laboratorio 3.

Desde la planilla Excel donde se descargaron los datos, y para una mejor visualización y tratamiento de los mismos, seleccionar las 5 primeras mediciones de ese laboratorio, copiarlas y pegarlas en la misma planilla, (por ejemplo, de F1 a J5) con el pegado especial de Excel, eligiendo Transponer. Quedará una fila con las 5 mediciones correspondientes a las obtenidas durante el primer día. Continuar seleccionando las 5 mediciones siguientes del Laboratorio 3 y transponiendo debajo de la primera fila. Al terminar, obtendrán una matriz de 20 filas por 5 columnas.

Copiar en GeoGebra todos los datos descargados para resolver los ejercicios 2, 3 y 4:

2. Considerar las 100 mediciones del Laboratorio 1 como la Población 1 y organizar los datos de la Población 1:

a) Agrupar los datos por intervalos regulares.

b) Construir la gráfica de frecuencias correspondiente a esta Población 1, y calcular su media, su varianza y su desviación estándar.

c) Seleccionar 30 muestras aleatorias independientes de tamaño 40.

d) Para cada una de las muestras, calcular su media y su varianza. Crear una lista con las medias muestrales así obtenidas y otra lista para las varianzas.

e) Agrupar por intervalos las medias obtenidas en cada muestra y representarlas gráficamente.

f) ¿Qué elementos da la teoría respecto de la distribución de la media muestral? ¿Coincide con la gráfica del inciso e)?

g) Comparar respectivamente, la media y la varianza de la Población 1 con la media de las medias muestrales y la media de las varianzas de las medias muestrales. Justificar los resultados obtenidos.

h) Utilizar la desviación estándar de las medias muestrales de tamaño 40 para compararla con el cociente ente la desviación estándar de la Población 1 y la raíz cuadrada del tamaño de las muestras. Desde la teoría, ¿Cómo justifican el resultado de la comparación?

 

4. 5. Resolver problemas aplicando estimaciones o pruebas de hipótesis

 

En esta resolución se identifican: parámetro y estadístico, distribución del estimador del parámetro en cuestión, error de muestreo y confiabilidad, esperanza y varianza del estadístico seleccionado, hipótesis nula y alternativa, nivel de significación, estimador y estimación, valor crítico y valor observado.

 

4.5.1. Fundamentación de la Actividad 5

Es importante que el estudiante pueda ubicarse en el contexto que está trabajando, para poder diferenciar parámetro de estadístico y estadístico de estimación. En esta diferenciación, se destaca que el vocablo “estadístico” tiene dos acepciones: una, como variable aleatoria, con su respectiva distribución de probabilidades, y la otra, como “valor observado” que es el valor calculado con los datos de la muestra. Reconocer que el valor observado es uno de los valores que puede tomar la variable aleatoria asociada, contribuye a la justificación de la comparación de los valores observados con los valores teóricos de las tablas de probabilidades. El estudiante puede comprobar que la estimación puntual es el valor observado del estadístico que estima a un parámetro. Con la simulación de una población, este parámetro puede calcularse, y al ser conocido, compararse con el valor obtenido en la estimación a partir de la muestra seleccionada, calcular el error de muestreo, verificar si el parámetro a estimar pertenece al intervalo de confianza obtenido en la muestra y, verificar hipótesis entre las actividades más relevantes.

 

4.5.2. Enunciado de la Actividad 5 para trabajar en grupos

Continuar con los datos proporcionados para la Actividad 4.

1. Seleccionar una muestra aleatoria de tamaño 20 de la Población 4. Considerar conocida la varianza de la Población 4.

a) Estimar por punto la media poblacional. ¿Es una buena estimación? Justificar la respuesta con el cálculo del error de muestreo. ¿Siempre es posible calcular este error? Justificar.

b) Estimar el promedio real de la tensión de rotura, con un intervalo del 95% de confianza. El intervalo hallado: ¿cumple con ser uno de los 95 intervalos donde se encuentra el promedio real de la tensión de rotura? Justificar.

c) Profesionales del Laboratorio 4 afirman que el promedio real de la tensión de rotura de este tipo de probetas, está dado por la media de la Población 4. Contrasta la hipótesis que plantean estos profesionales a un nivel de significación del 5%, según los datos obtenidos en la muestra.

2. Seleccionar una muestra aleatoria de tamaño 15 de la Población 3 y suponiendo que la desviación estándar de la Población 3 no es conocida:

a) ¿Es posible estimar con un intervalo del 90% de confiabilidad, el promedio real de la tensión de rotura? Justifica tu respuesta y, si es posible, encuentra el intervalo para la muestra seleccionada.

b) Profesionales del Laboratorio 3 afirman que el promedio real de la tensión de rotura de este tipo de probetas, está dado por la media de la Población 3. Contrasta la hipótesis que plantean estos profesionales a un nivel de significación del 1%, según la media obtenida en la muestra.

 

5. CONCLUSIONES

 

El diseño de esta propuesta se fundamentó en utilizar los resultados de aprendizaje de la asignatura como puntos de llegada de un camino que aplicó, en todo su recorrido, una enseñanza contextualizada y significativa de la estadística, con la intención de contribuir a resolver las problemáticas detalladas en los antecedentes presentados en este artículo, las cuales están referidas a la comprensión de los conceptos asociados a las ideas fundamentales de la estadística para el aprendizaje de la Inferencia Estadística. Es sabido que el abordaje tradicional de los contenidos de probabilidad y de estadística, dificulta la comprensión de la vinculación entre ellos. La estrategia desarrollada en esta propuesta utiliza la inferencia informal, en una primera fase, se plantean conjeturas sobre la información muestral obtenida para aplicar, en una segunda fase, técnicas de pruebas de hipótesis y estimaciones sobre los parámetros trabajados.

Considerar un antes y un después de la experiencia aleatoria, resulta un aspecto central para vincular la enseñanza de la estadística y la probabilidad, junto a ambientes computacionales a través de simulaciones. La ley de los grandes números emerge en forma natural en estos escenarios, y todas estas actividades contribuyen a disminuir la confusión entre parámetro y estadístico, a diferenciar distribuciones empíricas de teóricas, y a darle sentido a la comparación entre el valor crítico y el observado, para la toma posterior de decisiones. De esta manera, al momento que se abordan los contenidos de Inferencia Estadística, los conceptos de probabilidad y los de estadística que fueron vinculados a través de esta metodología de trabajo, contribuyen a darle sentido y significado a cada uno de los pasos utilizados en la resolución de problemas de estimación y pruebas de hipótesis.

En el marco de esta propuesta, se concluye que continuar con el diseño de este tipo de actividades que favorecen la comprensión de la Inferencia Estadística al tratarla como un proceso, proporciona al estudiante un hilo conductor que une, no sólo todas las etapas del método estadístico, sino también articula los conceptos probabilísticos y estadísticos utilizados.

En futuras etapas, se espera poder analizar el impacto de esta metodología de trabajo en el proceso de aprendizaje, a través del desempeño académico de los estudiantes. Para esto, se prevé la aplicación de una rúbrica que evalúe los resultados de aprendizaje mencionados.

 

REFERENCIAS BIBLIOGRÁFICAS

 

Alvarado, H. y Batanero, C. (2007). Dificultades de comprensión de la aproximación normal a la distribución binomial. Números, 67, 1-7.

Alvarado, H., Galindo, M. y Retamal, L.M. (2013). Comprensión de la distribución muestral mediante configuraciones didácticas y su implicación en la inferencia estadística. Enseñanza de las Ciencias, 31(2), 75-91.

Alvarado, H., Galindo, M. y Retamal, L.M. (2018). Evaluación del aprendizaje de la estadística orientada a proyectos en estudiantes de ingeniería. Educación Matemática, 30(3), 151-183. https://doi.org/10.24844/em3003.07

Batanero, C., Tauber, L. y Sánchez, V. (2001). Significado y comprensión de la distribución normal en un curso introductorio de análisis de datos. Quadrante, 10(1), 59-91.

Batanero, C. (2013a) Sentido estadístico: componentes y desarrollo. En J.M. Contreras, G.R. Cañadas, M.M. Gea y P. Arteaga (Eds.), Actas de las Jornadas Virtuales en Didáctica de la Estadística, Probabilidad y Combinatoria (pp. 55-61). Universidad de Granada.

Batanero, C. (2013b). Del análisis de datos a la inferencia: reflexiones sobre la formación del razonamiento estadístico. Cuadernos de Investigación y Formación en Educación Matemática, 8(11), 277-291.

Behar, R. y Yepes, M. (2007). Estadística: un enfoque descriptivo. Talleres gráficos Impresora Feriva.

Chance, B., Ben-Zvi, D., Garfield, J. y Medina, E. (2007). The role of technology in improving student learning of statistics. Technology Innovations in Statistics Education, 1(1), 1-26.

Chance, B., del Mas, R. y Garfield, J. (2004). Reasoning about sampling distributions. En D. Ben-Zvi y J. Garfield (Eds.), The Challenge of developing Statistical Literacy, Reasoning and Thinking (pp. 295-323). Kluwer Academic Publishers

CONFEDI (2016). Competencias y Perfil del Ingeniero Iberoamericano, Formación de Profesores y Desarrollo Tecnológico e Innovación (Documentos Plan Estratégico ASIBEI). ASIBEI. https://www.acofi.edu.co/noticias/competencias-y-perfil-del-ingeniero-iberoamericano-formacion-de-profesores-y-desarrollo-tecnologico-e-innovacion/

CONFEDI (2018). Propuesta de estándares de segunda generación para la acreditación de carreras de ingeniería en la República Argentina “Libro Rojo de CONFEDI”. Universidad FASTA Ediciones.

del Mas, R., Garfield, J. y Chance, B. (2004, abril). Using assessment to study the development of students’ reasoning about sampling distributions. Annual Meeting of the American Educational Research Association, California.

Figueroa, S. y Aznar, M. (2017). Significados personales sobre la vinculación entre una variable estadística y su variable binomial asociada en el contexto de un problema. En J.M. Contreras, P. Arteaga, G. R. Cañadas, M.M. Gea, B. Giacomone y M. M. López-Martín (Eds.), Actas del Segundo Congreso International Virtual sobre el Enfoque Ontosemiótico del Conocimiento y la Instrucción Matemáticos (pp. 1-10). Universidad de Granada.

Godino, J. y Batanero, C. (1994), Significado institucional y personal de los objetos matemáticos, Recherches en Didactique des Mathématiques, 14(3), 325-355.

Inzunza, S. (2006). Significados que estudiantes universitarios atribuyen a las distribuciones muestrales en un ambiente de simulación computacional y estadística dinámica. [Tesis doctoral, Departamento de Matemática Educativa del Centro de Investigación y de Estudios Avanzados del IPN].

Inzunza, S. (2007). Recursos de internet para apoyo de la investigación y la educación estadística. Revista Iberoamericana de Educación, 41(4), 1-12.

Inzunza, S. (2017). Significado institucional de las distribuciones muestrales en libros de texto universitarios. En J.M. Contreras, P. Arteaga, G.R. Cañadas, M.M. Gea, B. Giacomone y M.M. López-Martín (Eds.), Actas del Segundo Congreso International Virtual sobre el Enfoque Ontosemiótico del Conocimiento y la Instrucción Matemáticos (pp. 1-10). Universidad de Granada.

Kowalski, V., Posluszny, J., López, J., Erck, I. y Enriquez, H. (2016). Formación por competencias en ingeniería: ¿Camino o destino? Revista Argentina de Ingeniería, 5(7), 130-141.

Meyer, R. (2005). Funcionamiento didáctico del Saber. La inferencial estadística como metodología y la formación de formadores en educación. [Tesis Doctoral en Educación, Universidad Católica de Santa Fe].

Meyer, R., Debiaggi, M. y Giménez, N. (2008). La inferencia estadística como metodología. Análisis de contenido de ideas fundamentales. Ciencias Económicas, 2(6), 29-46.

Olivo, E. y Batanero, C. (2007). Un estudio exploratorio de dificultades de comprensión del intervalo de confianza. UNION, 12, 37-51.

Ramírez, G. (2008). Formas de razonamiento que muestran estudiantes de maestría de matemática educativa sobre la distribución normal mediante problemas de simulación de fathom. Revista Electrónica de Investigación en Educación en Ciencias, 3(1), 10-23

Restrepo, G. y Lopera, M.A. (2015). CDIO: una gran estrategia de formación en ingeniería. Revista Ingeniería y Sociedad, 9, 33-39.

Retamal, M.L. (2013). Enseñanza de la estadística mediante proyectos de iniciación científica en estudiantes universitarios. En Instituto Tecnológico de Costa Rica, Costa Rica (Ed.), III Encuentro sobre Didáctica de la Estadística, la Probabilidad y el Análisis de Datos (pp. 1-12). Instituto Tecnológico de Costa Rica.

Retamal, M.L., Alvarado, H. y Rebolledo, R. (2007). Understanding of sample distributions for a course on statistics for engineers. Ingeniare, 15, 6-17.

Ruiz, B. y Albert, J. (2013). La relación entre la variable aleatoria y la variable estadística: un análisis epistemológico disciplinar. En J.M. Contreras, G.R. Cañadas, M.M. Gea y P. Arteaga (Eds.), Actas de las Jornadas Virtuales en Didáctica de la Estadística, Probabilidad y Combinatoria (pp. 383-390). Universidad de Granada.

Sánchez, N. y Ruiz, B. (2017) La inferencia informal en la enseñanza de la estadística. Una propuesta por medio del estudio de clases. En A. Rosas (Ed.), Avances en Matemática Educativa. El profesor investigador Nº6 (pp. 117-133). Lectorum.

Santarrone, M. y Meyer, R. (2020, octubre). Población estadística. Una idea fundamental en la inferencia estadística paramétrica [Sesión de congreso]. XIV Jornadas de Investigación de la Facultad de Ciencias Económicas de la Universidad Nacional del Litoral de la República Argentina. Santa Fe, Argentina.

Terán, T. y Ciminari, J. (2019). Los errores en la resolución de situaciones problemáticas de inferencia estadística como principal obstáculo en la didáctica de la estadística. En J.M. Contreras, M.M. Gea, M.M. López-Martín y E. Molina-Portillo (Eds.), Actas del Tercer Congreso Internacional Virtual de Educación Estadística (pp. 1-8). FQM126.

Wild, C.J. y Pfannkuch, M. (1999). Statistical thinking in empirical enquiry, International Statistical Review, 67, 223-265.

 

Como citar:

Figueroa, S.M. y Distéfano, M.L. (2023). Estrategia para la enseñanza de la inferencia en Ingeniería: fundamentos para su diseño. Revista de Educación Estadística, 2(1), 1-28. https://doi.org/10.29035/redes.2.1.7

 

Esta obra está bajo una licencia de Creative Commons
Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional.