IDEAS ESTADÍSTICAS FUNDAMENTALES EN LA FORMACIÓN DEL PROFESOR DE MATEMÁTICAS DE EDUCACIÓN SECUNDARIA EN MÉXICO

Revista de Educación Estadística

https://revistaeduest.ucm.cl/

Vol. 4, pp. 1-19, ene. 2025 - dic. 2025

ISSN 2810-6164

DOI: https://doi.org/10.29035/redes.4.1.8

IDEAS ESTADÍSTICAS FUNDAMENTALES EN LA FORMACIÓN DEL PROFESOR DE MATEMÁTICAS DE EDUCACIÓN SECUNDARIA EN MÉXICO

Ideias estatísticas fundamentais na formação de professores de matemática do ensino secundário no México

Fundamental statistical ideas in the training of secondary education mathematics teachers in Mexico

Miguel Ángel Verástegui Gutiérrez1

Universidad Autónoma de Zacatecas (Zacatecas, México)

José Iván López-Flores2

Universidad Autónoma de Zacatecas (Zacatecas, México)

*Jaime I. García-García3

Universidad Metropolitana de Ciencias de la Educación (Santiago, Chile)

Resumen

En este estudio se analiza la presencia de las ideas estadísticas fundamentales durante la formación inicial del profesor de matemáticas de Educación Secundaria en México. La investigación se enmarca en una metodología cualitativa y se utiliza como método el análisis de contenido para analizar la presencia de dichas ideas en las actividades que se proponen en los programas de estudio de los cursos vinculados a la estadística y la probabilidad, a saber: Tratamiento de la información, Pensamiento estocástico y Estadística inferencial. Los resultados nos permiten concluir que estas ideas están presentes a lo largo de los tres cursos, donde se destacan datos, representación y probabilidad; mientras que asociación y modelado, así como variación, son aquellas que tienen menor presencia. En general, se concluye que es importante fortalecer las ideas estadísticas fundamentales en la formación inicial del profesor de matemáticas de Educación Secundaria, para que pueda transmitirlas adecuadamente a sus futuros estudiantes y, con ello, promover el desarrollo del razonamiento estadístico.

Palabras clave: Educación secundaria, Estadística, Formación de profesores, Programa de estudios.

Resumo

Este estudo analisa a presença de ideias estatísticas fundamentais durante a formação inicial de professores de matemática do ensino médio no México. A pesquisa está enquadrada em uma metodologia qualitativa e a análise de conteúdo é usada como método para analisar a presença dessas ideias nas atividades propostas nos programas de estudo dos cursos relacionados à estatística e à probabilidade, a saber: Processamento de Informações, Pensamento Estocástico e Estatística Inferencial. Os resultados nos permitem concluir que essas ideias estão presentes nos três cursos, onde se destacam dados, representação e probabilidade; enquanto associação e modelagem, bem como variação, são as que têm menor presença. Em geral, concluímos que é importante reforçar as ideias estatísticas fundamentais na formação inicial dos professores de Matemática do Ensino Médio, para que eles possam transmiti-las adequadamente a seus futuros alunos e, assim, promover o desenvolvimento do raciocínio estatístico.

Palavras-chave: Ensino secundário, Estatística, Formação de professores, Currículo.

Abstract

This study analyzes the presence of fundamental statistical ideas during the initial training of secondary school mathematics teachers in Mexico. The research is framed within a qualitative methodology and content analysis is used as a method to analyze the presence of such ideas in the activities proposed in the curricula of courses linked to statistics and probability, namely: Information Processing, Stochastic Thinking and Inferential Statistics. The results allow us to conclude that these ideas are present throughout the three courses, where data, representation and probability stand out; while association and modeling, as well as variation, are those that have less presence. In general, we conclude that it is important to strengthen the fundamental statistical ideas in the initial training of the mathematics teacher in Secondary Education, so that they can adequately transmit them to future students and, thus, promote the development of statistical reasoning.

Keywords: Secondary education, Statistics, Teacher training, Curriculum.

Recibido: 10/11/2024 - Aceptado: 13/06/2025

1. INTRODUCCIÓN

En recientes investigaciones se ha observado la importancia que juegan las Ideas Estadísticas Fundamentales (IEF de aquí en adelante) dentro del proceso de enseñanza y aprendizaje de la estadística en los diferentes niveles educativos, siendo un área de investigación en Educación Estadística que requiere de ser estudiada, justificándose en las diversas aplicaciones que demanda la estadística como ciencia de los datos (Batanero et al., 2011; Bianchini, 2022; Garfield y Ben-Zvi, 2008; Tauber et al., 2019).

Dada la presencia de las IEF en el currículo de Educación Básica, recae en el profesor de matemáticas la responsabilidad de garantizar su enseñanza efectiva, al ser el encargado de llevar al aula los contenidos correspondientes a estos temas (Batanero et al., 2011). Por su parte, Estrella (2017) señala la importancia del desarrollo de las IEF y del razonamiento estadístico en los estudiantes de los diversos niveles educativos, atribuyendo esta tarea a los profesores frente a grupo. En ese sentido, es necesaria una formación especializada en el profesorado, que contemple no solo el área disciplinar, sino también un conocimiento profundo de cómo transmitir conceptos e ideas estadísticas en el alumnado, considerando el uso de softwares educativos que favorezcan el análisis de los datos y la toma de decisiones (Zamora et al., 2022).

En la literatura se han reportado investigaciones que señalan algunas dificultades presentes en la formación estadística que reciben los profesores de matemáticas y propuestas para mejorar la enseñanza en el aula (Alsina et al., 2020; Micheli, 2010; Zamora et al., 2022). Una de estas propuestas consiste en que la formación del profesor debe distinguirse por la promoción de su razonamiento estadístico y su comprensión conceptual a través del proceso investigativo estadístico, apoyado de la exploración y análisis de datos en contexto y del uso de la tecnología (Estrella, 2017).

En relación con las IEF dentro del aula, algunas investigaciones se han dado a la tarea de analizar su presencia y cómo se incorporan en los libros de texto y los currículos educativos de algunos países (Inzunza y Rocha, 2021; Salcedo, 2019; Salcedo et al. 2021; Vásquez y Cabrera, 2022).

Por ejemplo, Salcedo (2019) señala que las IEF presentes en las actividades de los libros de texto venezolanos de primaria y secundaria no parecen contribuir a la formación estadística del ciudadano, debido a su baja demanda cognitiva y solo se trabajan dos ideas: análisis exploratorio de datos y modelación de información por probabilidad (Batanero y Borovcnik, 2016). En Salcedo et al. (2021) se indica que en los libros de texto de primaria Nicaragua y Venezuela se abordan únicamente tres de las siete IEF propuestas por Burrill y Biehler (2011): representación, distribución y modelos de probabilidad en los libros nicaragüenses; y dato, representación y modelos de probabilidad en los libros venezolanos. Además, los autores señalan que en los libros de texto de ambos países se pone mayor énfasis en tareas de procedimiento sin conexión (algorítmicas).

Vásquez y Cabrera (2022) establecen la importancia de abordar las IEF desde edades tempranas, de manera progresiva y con distintos niveles de profundidad acorde a su edad para desarrollar gradualmente la alfabetización estadística y probabilística en el alumnado. A la luz de examinar la presencia de las IEF en los currículos escolares de diferentes países (Estados Unidos, Australia, Singapur, Nueva Zelanda, España y Chile), en el caso de Educación Primaria, se identificó la presencia de las ideas de datos, representación, variación y distribución (Burrill y Biehler, 2011); mientras que, para el caso de Educación Primaria, notaron la presencia de todas las IEF en los currículos de Estados Unidos, Australia y Nueva Zelanda, siendo asociación y correlación, así como muestreo e inferencia, aquellas con menor predominancia.

Inzunza y Rocha (2021) comparten su preocupación en cuanto a la enseñanza de la estadística y probabilidad en Educación Media (Bachillerato), ya que en el currículo mexicano de este nivel educativo no se incluye la inferencia estadística. Además, los autores mencionan esta ausencia en la mayoría de los currículos escolares de los países latinoamericanos, a excepción de algunos como Chile, en los que se incluyen temas de muestreo e inferencia estadística, así como elementos de razonamiento inferencial, a partir del séptimo año. En el contexto mexicano, señalan que la idea de datos se trabaja desde Educación Preescolar hasta bachillerato; mientras que el azar está presente a partir de quinto año de Educación Primaria.

En un estudio reciente, Verástegui et al. (2023) analizan la presencia de las IEF (Burrill y Biehler, 2011) en las actividades propuestas en el curso de Estadística inferencial, en la formación del profesor de matemáticas de nivel secundaria, donde se establece que se promueven dichas ideas durante la preparación del profesorado.

A partir de esta breve revisión de literatura, es posible observar que la comunidad de Educación Estadística se ha interesado por estudiar la presencia de las IEF en los currículos escolares de los niveles educativos en diferentes países, así como las implicaciones que esto conlleva en el proceso de enseñanza-aprendizaje de la estadística y en la formación del futuro profesor de matemáticas.

A partir de lo anterior, este trabajo tuvo como objetivo analizar la presencia de las IEF en el currículo educativo para la formación del profesorado de matemáticas de Educación Secundaria en México, considerando los programas de estudio de los cursos vinculados a la probabilidad y la estadística: 1) Tratamiento de la información (Ti), 2) Pensamiento estocástico (Pe) y 3) Estadística inferencial (Ei). Cabe señalar que esta investigación es una ampliación del estudio desarrollado en Verástegui et al. (2023), con el propósito de indagar cómo se plantea el desarrollo de las IEF durante la formación inicial de dicho profesorado.

2. LAS IDEAS ESTADÍSTICAS FUNDAMENTALES

Existen diversas perspectivas acerca de cuáles son las IEF; por ejemplo, las propuestas por Kilpatrick et al. (2001) y Watson (2006) están enfocadas en Educación Primaria y parte de la Secundaria, las de Burrill y Biehler (2011) y Batanero y Borovcnik (2016) están pensadas para Educación Secundaria y Educación Media (Bachillerato), mientras que las de Garfield y Ben-Zvi (2008) se centran en un primer curso de estadística en Educación Superior (Tabla 1).

Tabla 1

Distintas propuestas sobre las ideas estadísticas fundamentales

Kilpatrick et al., (2001)	Watson (2006)	Burrill y Biehler (2011)	Batanero y Borovcnik (2016)	Garfield y Ben-Zvi (2008)
Describir datos	Colección de datos	Datos	Análisis exploratorio de datos	Datos
Organizar datos	Reducción de datos	Datos
Representar datos	Representación gráfica	Representación
Análisis de datos	Variabilidad	Distribución		Distribución
		Distribución		Centro
		Variación		Variabilidad
Probabilidad de un evento	Probabilidad	Modelos de probabilidad para procesos de generación de datos	Modelación de información por probabilidad	Aleatoriedad
Comparaciones de probabilidades entre espacios muestrales
Probabilidad condicional
Independencia de un evento
	Muestreo	Muestreo e inferencia	Muestreo e inferencia	Muestreo
	Inferencia	Muestreo e inferencia	Muestreo e inferencia	Inferencia estadística
		Relaciones de asociación y modelado entre dos variables	Exploración y modelación de la asociación	Modelos estadísticos

Para esta investigación adoptamos la propuesta de Burrill y Biehler (2011), quienes señalan que estas IEF debieran “enseñarse en las matemáticas escolares y todo alumno debería conocerlas al salir de la escuela secundaria” (p. 58). Dichos autores se basan en algunos de los criterios expuestos por Heymann (2003) con la finalidad de realizar conexiones entre la estadística y la cotidianeidad, y con ello, lograr una comprensión profunda en el estudiantado. La propuesta de estos autores está compuesta por las siguientes ideas:

1. Datos. En el salón de clase se trabajan los datos en la “visualización de números” y en el estudio de las funciones; sin embargo, rara vez se abordan los datos en un contexto. En este sentido, esta idea incluye los diferentes tipos de datos, las formas de recopilarlos y su medición.

2. Variación. La variación en estadística consiste en cómo medir y controlar la variabilidad. Los datos reales son contextuales, de tal forma que presentan incertidumbre y error.

3. Distribución. Esta idea se desarrolla en la enseñanza de la estadística, donde se contempla la tendencia de los datos y su dispersión. Así como el razonamiento de variables aleatorias y resúmenes en distribuciones de muestreo.

4. Representación. Esta idea requiere de la visualización de los datos, donde se utilizan gráficos o representaciones para identificar aspectos de los mismos datos (se incluye la noción de la transnumeración).

5. Relaciones de asociación y modelado entre dos variables. Se utiliza en particular para el análisis de datos cuantitativos bivariantes; además, se incluye la regresión para la modelización de asociaciones estadísticas.

6. Modelos de probabilidad para procesos de generación de datos. La extracción de muestras aleatorias a partir de datos de población y la variación entre muestras pueden modelarse a través de modelos de probabilidad. En este sentido, esta idea puede aprovecharse para enriquecerse con experiencias fenomenológicas, en las que la simulación puede desempeñar un papel trascendental.

7. Muestreo e inferencia. Las afirmaciones estadísticas sobre el margen de error y los intervalos de confianza se consideran ejemplos de inferencias a partir de la muestra.

En resumen, Burrill y Biehler (2011) proponen utilizar las ideas estadísticas de forma que se utilicen datos reales, realizar predicciones previas a calcular, formular preguntas sobre el azar con base en los datos, analizar diferentes tipos de distribuciones, utilizar la visualización como herramienta para aprender acerca de las relaciones, explorar diversas representaciones de los datos para comprender las relaciones y conexiones que mantienen las variables.

3. METODOLOGÍA

El enfoque metodológico del presente estudio es de tipo cualitativo (Cohen et al., 2002), donde se utiliza el análisis de contenido como técnica de investigación, sistemática y objetiva para la descripción e interpretación de diferentes tipos de documentos (Bernete, 2013); en nuestro caso, los programas de estudio de los cursos que se detallan a continuación.

3.1. Datos y contexto: currículo educativo para la formación del profesor de matemáticas

En México, los profesores de matemáticas de Educación Secundaria son formados según el Plan de estudios de la Licenciatura en Enseñanza y Aprendizaje de las Matemáticas en Educación Secundaria (LEAMES) (DGESPE, 2018). La malla curricular contiene tres cursos que están vinculados a la estadística y la probabilidad:

1. Tratamiento de la información (Ti). Esta asignatura se cursa durante el segundo semestre de la LEAMES y pretende favorecer el procesamiento de la información cualitativa/cuantitativa, así como la incorporación del discurso estadístico. Además, propone al razonamiento estadístico como uno de los elementos que preparan para la autoformación del ciudadano. El curso Ti se divide en tres unidades de aprendizaje: Elementos del análisis cuantitativo, distintas tendencias de medida y distribuciones de probabilidad (Secretaría de Educación Pública [SEP], 2018).

2. Pensamiento estocástico (Pe). Este curso se ubica en el tercer semestre de la LEAMES y tiene por objetivo contextualizar y fundamentar la práctica profesional a partir de los principios de los estocásticos como las variables aleatorias discretas y continuas y estadísticos para la resolución de problemas. El programa de la presente asignatura conforma tres unidades de aprendizaje: Fundamentos de la probabilidad, Teoría de la probabilidad e Introducción a los procesos estocásticos de variable aleatoria continua y discreta. (SEP, 2019).

3. Estadística inferencial (Ei). Por último, los profesores de matemáticas cursan la asignatura de Ei durante el quinto semestre según el plan de estudios, donde se estudian pruebas de hipótesis estadísticas sobre el comportamiento de poblaciones y muestras en contextos escolares y sociales. Además, este curso provee herramientas para la toma de decisiones en la vida personal y profesional, así como una metodología de investigación en el aula de clases. El curso se conforma de tres unidades de aprendizaje: Muestreo, Distribuciones de Probabilidad y Pruebas de Hipótesis. (SEP, 2020).

3.2. Fases del análisis de contenido

Para el análisis de contenido, consideramos las tres fases propuestas por Bernete (2013):

1. Trabajo previo a la obtención de los datos. En esta fase se eligieron las unidades de muestreo a analizar que fueron los programas de estudio de Ti, Pe y Ei. Cada uno de estos documentos se conforman de los siguientes elementos: propósito general, antecedentes, características, competencias del perfil de egreso, orientaciones para el aprendizaje y enseñanza, sugerencias de evaluación, unidades de aprendizaje, propósitos de las unidades, contenidos, actividades de aprendizaje generales y específicas, evidencias de las unidades, criterios de evaluación y bibliográfica básica y complementaria. Cabe mencionar que cada programa contiene tres unidades de aprendizaje, donde se sugieren actividades a desarrollar para el logro de los aprendizajes.

2. Extracción de datos. En la segunda fase se enlistaron y examinaron las actividades específicas y generales de cada uno de los programas de estudio. Los programas de Ei y de Pe contienen 39 actividades, respectivamente, mientras que el programa Ti sugiere 29 actividades.

3. Explotación de datos. Para esta última fase se identificaron las IEF presentes en las diferentes actividades de aprendizaje que se proponen en los tres programas de estudio (Ti, Pe, Ei). Después, se identificaron cuáles de estas estaban presentes en cada una de las unidades de aprendizaje. Por ejemplo, la idea de datos se presentó en al menos una de las actividades propuestas por unidad de aprendizaje.

4. RESULTADOS

En el análisis de las actividades que se proponen en los programas de estudio para la formación del profesor de matemáticas de Educación Secundaria en México, vinculados a la probabilidad y la estadística, se encontraron presentes algunas de las IEF a lo largo de las tres unidades de aprendizaje que conforman cada uno de los cursos (Ti, Pe y Ei).

4.1. Las IEF en el programa de estudio de Tratamiento de la información

Como se declaró anteriormente, el curso Ti busca que el profesor en formación reflexione sobre la naturaleza de la información, así como su organización, procesamiento y presentación de una manera óptima (SEP, 2018).

En la primera unidad de aprendizaje, Elementos de análisis cuantitativo, se interpreta información obtenida mediante fenómenos de la vida cotidiana, organizados en tablas y gráficos estadísticos. Se discrimina entre los diferentes métodos para el procesamiento y presentación de la información (SEP, 2018). En la Figura 1 puede observarse que se favorece la IEF de representación, donde se especifica que el estudiante elabora gráficos estadísticos. Mientras que la IEF de datos se ve favorecida en una de las actividades donde el estudiantado recurre a investigar sobre algún tema en específico, en este caso, el programa del curso Ti propone como tópico los intereses de los estudiantes, donde también se introduce la idea de muestreo.

Figura 1

Presencia de las IEF en algunas actividades propuestas en la primera unidad del programa Ti

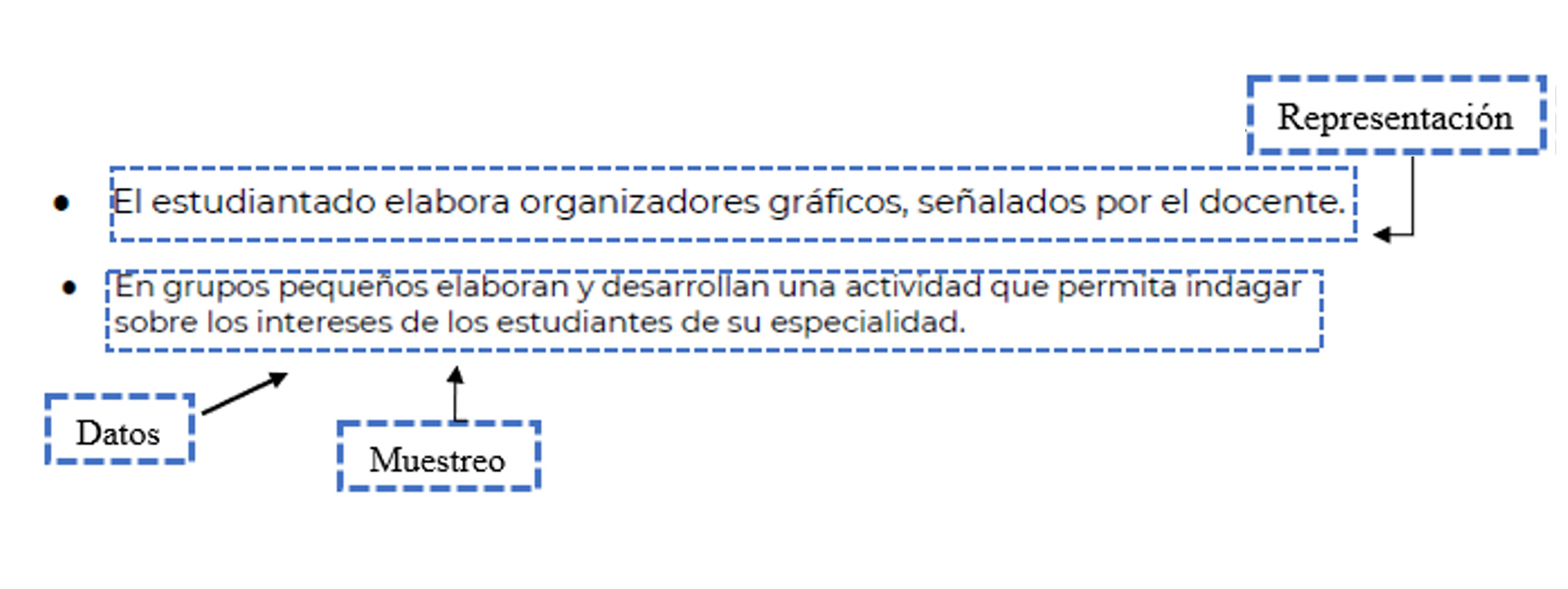
Fuente: SEP (2018, p. 17).

Figura 2

Presencia de las IEF en algunas actividades propuestas en la segunda unidad del programa Ti

Fuente: SEP (2018, p. 23).

En la segunda unidad de aprendizaje, Distintas tendencias de medida, se explican fenómenos cotidianos mediante la utilización de las medidas de tendencia central y dispersión. Se interpretan diversos aspectos de la realidad mediante el procesamiento y presentación de la información con el uso de diferentes técnicas de recolección de datos. En la Figura 2 se puede observar la presencia de algunas IEF como datos, donde se propone que los estudiantes utilicen herramientas tecnológicas para el procesamiento e interpretación de la información. La variación y la distribución pueden distinguirse en actividades donde los alumnos trabajan con medidas descriptivas como la media aritmética, mediana y moda; así como conceptos de variabilidad.

En la tercera unidad de aprendizaje, Distribuciones de probabilidad, se trabaja el análisis, resumen e interpretación de la información, además se indica realizar predicciones tomando en cuenta el comportamiento estandarizado de poblaciones y muestras aleatorias para la toma de decisiones. En la Figura 3 puede observarse que la mayoría de las IEF se presentan en esta última unidad del programa Ti. La probabilidad y distribución se hacen notar en la caracterización conceptual de términos como sesgo y normalidad. Podemos considerar esta última actividad como una introducción al estudio de la distribución normal, que ocupa espacio en el curso consecuente de Pe (SEP, 2019).

Figura 3

Presencia de las IEF en algunas actividades propuestas en la tercera unidad del programa Ti

Fuente: SEP (2018, p. 27-28).

4.2. Las IEF en las actividades de aprendizaje del programa de estudio de Pensamiento estocástico

El curso Pe aproxima a los futuros docentes en el estudio de los estocásticos, donde se abordan conceptos como los tipos de variables y se diferencian aquellos argumentos probabilísticos de los que no lo son (SEP, 2019).

A lo largo de la primera unidad de aprendizaje, Fundamentos de la probabilidad, se validan conjeturas acerca de diferentes fenómenos aleatorios con base en el análisis de información cuantitativa y cualitativa, a partir de juegos de azar y situaciones no deterministas (SEP, 2019). En la Figura 4 pueden notarse la presencia de IEF como la probabilidad, la cual destaca en las diferentes actividades, debido a la naturaleza de la predicción y el azar. En el caso de la IEF de datos, esta se encuentra en actividades que involucran recopilarlos mediante situaciones como los juegos azarosos. La representación se ubica en el análisis e interpretación de gráficos con la intención de predecir.

Figura 4

Presencia de las IEF en algunas actividades propuestas en la primera unidad del programa Pe

Fuente: SEP (2019, p. 24).

Figura 5

Presencia de las IEF en algunas actividades propuestas en la segunda unidad del programa Pe

Fuente: SEP (2019, p. 32).

Durante la segunda unidad de aprendizaje, Teoría de la probabilidad, se articulan la combinatoria, la estadística y la probabilidad con la finalidad de facilitar el análisis de una situación modelada (SEP, 2019). En la Figura 5 puede observase la presencia de dos IEF, probabilidad y datos. A diferencia de la unidad anterior, en esta se ausenta la idea de representación, debido a que no se explicita como tal en las actividades propuestas. En cuanto a la idea de probabilidad, que como ya se mencionó, es la que predomina, radica en el cálculo de probabilidad de ocurrencia a partir de eventos mutuamente excluyentes e independientes.

En la tercera unidad de aprendizaje Introducción a los procesos estocásticos de variable aleatoria continua y discreta, se reflexiona sobre los procesos de enseñanza y aprendizaje de la probabilidad desde el análisis de situaciones problema probabilísticas que involucran variables aleatorias continuas y discretas (SEP, 2019). En la Figura 6 se presentan las IEF que se encuentran en las actividades de la última unidad de aprendizaje del programa Pe. Permanece la idea de probabilidad en situaciones que implican eventos independientes. También puede notarse la presencia de la distribución, en el cálculo y análisis de ocurrencia de los diferentes eventos que contiene una situación, como el caso del problema de los circuitos de radares.

Figura 6

Presencia de las IEF en algunas actividades propuestas en la tercera unidad del programa Pe

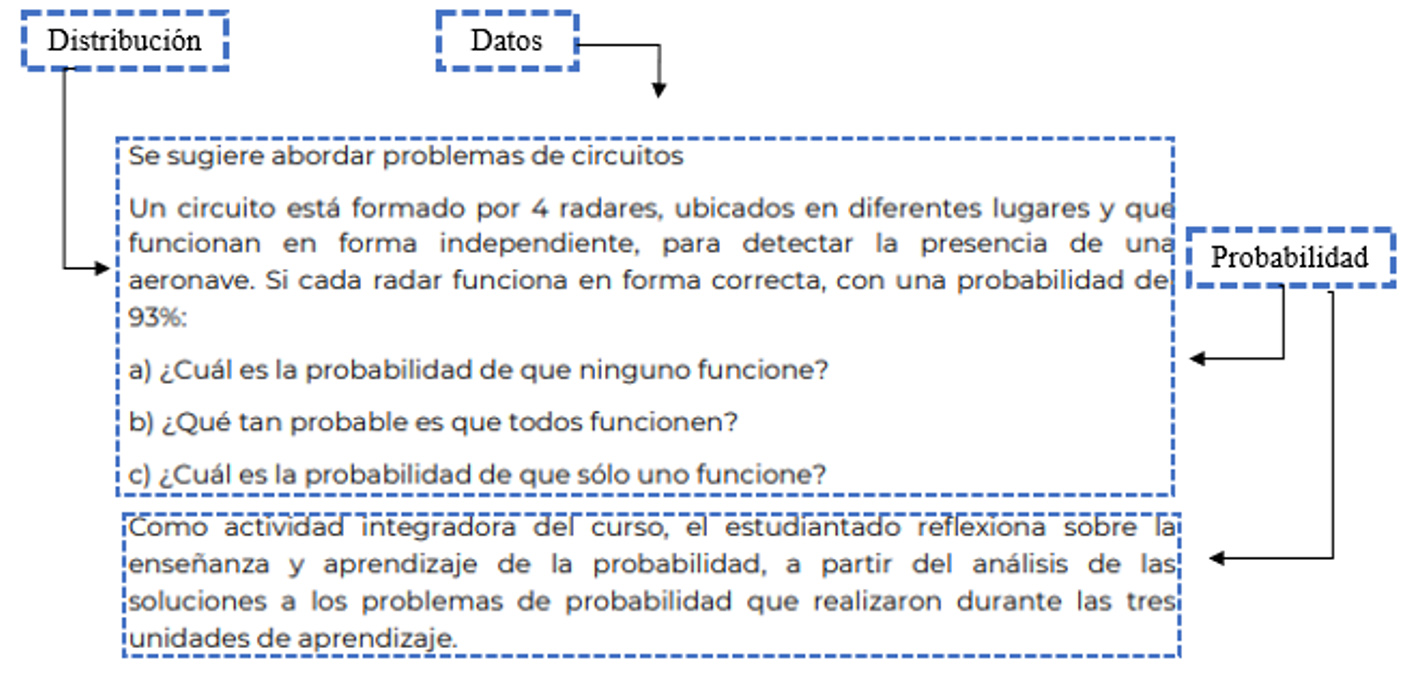
Fuente: SEP (2019, p. 40).

4.3. Las IEF en las actividades de aprendizaje del programa de estudio de Estadística inferencial

El curso Ei está enfocado en medir, modelar, predecir e inferir fenómenos aleatorios, con la intención de tomar decisiones informadas en diversas situaciones. Además, se busca que el futuro profesor utilice la inferencia estadística como una herramienta multidisciplinar en la tarea del quehacer docente y la investigación educativa (SEP, 2020).

En la primera unidad de aprendizaje, Muestreo, las actividades se centran en la lectura de información estadística acerca de los diferentes estudios en el campo educativo en México, para caracterizar al estudiantado de la Educación Básica, con el propósito de hacer inferencias sobre el comportamiento de una variable en una población (SEP, 2020). En la Figura 7 se expone la presencia de la mayoría de las IEF que se encuentran en las actividades de la primera unidad del curso Ei. Es posible observar que ideas como datos, muestreo e inferencia abarcan más de una de las actividades propuestas, especialmente cuando se trata de recopilar información mediante bases de datos o utilizando métodos de recolección, así como resultados de evaluación de estudiantes de Educación Básica, donde también se presenta la variación y distribución. Es importante destacar que la idea de asociación se presenta por primera vez en la formación inicial del profesor en el análisis de gráficos de regresión lineal.

Figura 7

Presencia de las IEF en algunas actividades propuestas en la primera unidad del programa Ei

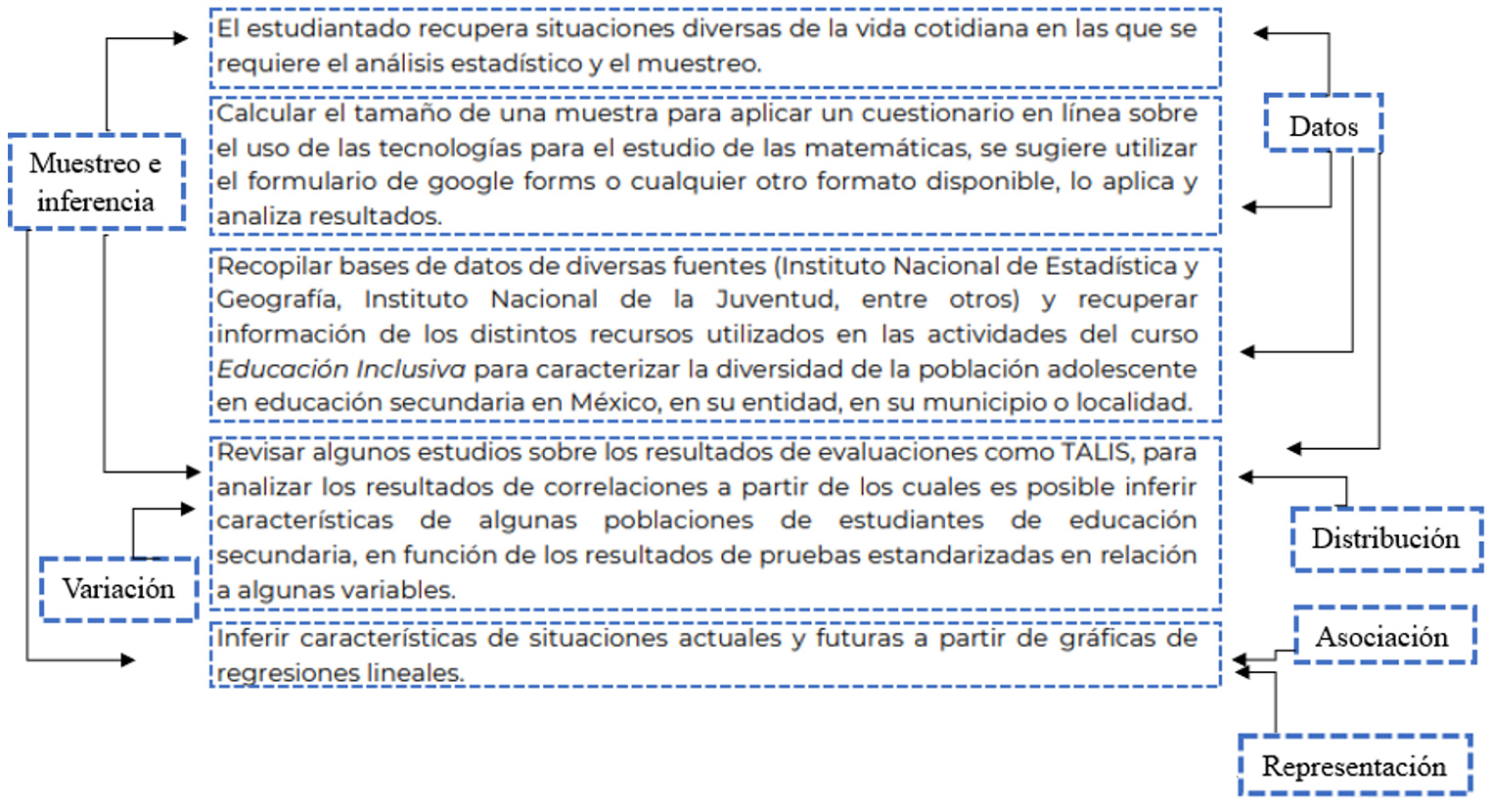
Fuente: SEP (2020, p. 22).

En la segunda unidad de aprendizaje, Distribuciones de probabilidad, se recuperan diversas situaciones que ocupan ser modeladas mediante distribuciones de probabilidad con respecto al tipo de variables que estas involucran (SEP, 2020). En la Figura 8 puede observarse que se encuentran casi todas las IEF, a excepción de asociación. En esta unidad, las ideas de probabilidad, datos y distribución abarcan más de una actividad, esto se justifica en que se estudian las diferentes distribuciones de probabilidad, tanto de variables aleatorias continuas como discretas. La idea de representación se fundamenta en la utilización de la curva de Gauss para visualizar el comportamiento de una distribución normal. En cuanto a la variación, muestreo e inferencia, se usa el análisis estadístico en el diseño de propuestas didácticas.

Figura 8

Presencia de las IEF en algunas actividades propuestas en la segunda unidad del programa Ei

Fuente: SEP (2020, p. 32).

Figura 9

Presencia de las IEF en algunas actividades propuestas en la tercera unidad del programa Ei

Fuente: SEP (2020, p. 41).

En la tercera unidad de aprendizaje, Prueba de hipótesis, se continúa estudiando las distribuciones de probabilidad para las pruebas de hipótesis de muestras pequeñas con el propósito de tomar decisiones sobre cuándo aceptar o rechazar una hipótesis de investigación (SEP, 2020). En la Figura 9 se expone la presencia de casi todas las IEF en las actividades que se sugieren en el programa del curso Ei. En dichas actividades se propone realizar pruebas de hipótesis, lo cual involucra IEF como muestreo e inferencia, variación, distribución, probabilidad y representación. El trabajo con datos reales continúa mediante la recuperación de resultados de evaluación.

4.4. Las IEF en la formación del profesor de matemáticas

Durante la formación del profesor de matemáticas se estudian tres cursos correspondientes a la estadística y probabilidad, donde se abordan actividades que involucran la presencia de IEF, lo cual puede observarse en la Tabla 2.

Tabla 2

Presencia de las IEF en las actividades de los programas de estudio para la formación estadística y probabilística del profesor de matemáticas

Idea estadística fundamental (IEF)	Tratamiento de la información			Pensamiento estocástico			Estadística inferencial			Presencia de la IEF (%)
Idea estadística fundamental (IEF)	U1	U2	U3	U1	U2	U3	U1	U2	U3	Presencia de la IEF (%)
Variación		X	X				X	X	X	55,6
Distribución		X	X			X	X	X	X	66,7
Representación	X	X	X	X			X	X	X	77,8
Asociación							X			11,0
Probabilidad			X	X	X	X	X	X	X	77,8
Muestreo e inferencia	X	X	X				X	X	X	66,7

Con base en el análisis de las actividades que conforman los tres programas de formación del profesor de matemáticas, podemos establecer que la IEF de datos es la que se encuentra presente a lo largo de todos los cursos que implican a la estadística y la probabilidad. Esta se trabaja en actividades donde se utilizan diferentes métodos para la recopilación de datos, el análisis de información estadística y el uso de recursos tecnológicos para el procesamiento de la información.

Las ideas de representación y probabilidad están presentes en un 77,8% de las unidades del estudio. La representación se observa mayormente favorecida en el curso Ti, donde se usan diferentes formas para representar los datos, como lo son las tablas y los gráficos estadísticos; mientras que, en el curso de Ei se presenta mayormente en las pruebas de hipótesis y las distribuciones de probabilidad, cuando se recurre a la curva normal.

La idea de probabilidad se trabaja con más frecuencia en el curso Pe y Ei, donde se aprovecha en actividades que involucran el cálculo de probabilidades para diferentes tipos de eventos, así como en el análisis de distribuciones de probabilidad para las variables aleatorias continuas y discretas.

Las ideas de distribución y muestreo e inferencia se abordan en el 66,7% de las unidades analizadas. Ambas se favorecen mayormente en los cursos de Ti y Ei. La distribución se aprovecha en el análisis estadístico, así como en las diferentes distribuciones de probabilidad.

En cuanto a la idea de muestreo e inferencia, esta no se presenta en el curso Pe, pero su estudio se inicia en las actividades que se proponen en el programa Ti. En suma, se presenta con más frecuencia en el curso Ei, donde se calcula el tamaño de una muestra, se infieren características sobre la población de estudiantes de Educación Básica, entre otras.

La idea de variación tiene un 66,7% de presencia en la formación del profesor de matemáticas. Esta se favorece en los cursos de Ti y Ei, donde las actividades propuestas involucran la toma de decisiones a partir del análisis y comparación, en dos o más conjuntos de datos, en la prueba de hipótesis, en las distribuciones de probabilidad y en el análisis de la información que se recaba mediante los diferentes métodos de recopilación.

Por último, se encuentra la idea de asociación que solo se presenta en un 11,1% de las unidades analizadas. En concreto, se presenta en la primera unidad del curso Ei; esta se aborda en actividades donde implica el análisis de la regresión lineal y el cálculo del coeficiente de correlación.

5. CONCLUSIONES

En esta investigación se analizaron las IEF y cómo se presentan en las actividades propuestas en los tres programas de estudio correspondientes a los cursos que involucran la estadística y la probabilidad: Tratamiento de la información (Ti), Pensamiento estocástico (Pe) y Estadística inferencial (Ei). Los resultados obtenidos señalan que todas las ideas propuestas por Burrill y Biehler (2011) se encuentran presentes al menos una vez a lo largo de la formación del profesor de matemáticas de Educación Secundaria en México. Es importante aclarar que cuando una IEF se presenta en alguna de las unidades de aprendizaje, esta puede presentarse parcial o completa. Por ejemplo, el muestreo e inferencia se encuentra presente en el curso Ti y Ei. No obstante, esta idea tiene mayor presencia en el último curso.

En las actividades propuestas en el programa del curso Ti predominan ideas como datos, representación, muestreo e inferencia, aunque esta última idea se limita al muestreo aleatorio. También ocupan espacio la variación y distribución en dos de las tres unidades de aprendizaje. La idea de probabilidad se encuentra en la última unidad de aprendizaje, esto con el objetivo de introducir a los estudiantes en el curso consecuente de Pe. No obstante, se puede notar la ausencia de la idea de asociación.

En el curso Pe predomina la idea de probabilidad, por la naturaleza del curso, por lo que la presencia de las otras IEF en este curso es limitada. Esto no significa que no se favorezcan las ideas o que el curso sea carente, sino que consideramos pertinente y necesario volver a analizar el programa de Pe, con un enfoque estocástico, donde se utilice otra propuesta de IEF, como la de Kilpatrick et al. (2001), o incluso considerar las ideas estocásticas fundamentales propuestas por Heitele (1975), con el objetivo de detallar cómo se trabajan las ideas en este curso y, con ello, complementar y enriquecer este trabajo de investigación.

En el curso Ei se concentran todas las IEF a lo largo de las actividades propuestas en las tres unidades de aprendizaje que conforman el curso (Verástegui et al., 2023). Sin embargo, la idea de asociación solo se presenta en la primera unidad de aprendizaje cuando se aborda la correlación y la regresión lineal.

En general, podemos concluir que se abordan las IEF propuestas por Burrill y Biehler (2011) en la formación inicial del profesor de matemáticas de Educación Secundaria en México. Este resultado coincide con los hallazgos de Vásquez y Cabrera (2022), con respecto a que se abordan todas las IEF en los currículos escolares de Educación Primaria de Estados Unidos, Australia y Nueva Zelanda. Sin embargo, dista de los reportados en Salcedo (2019) y en Salcedo et al. (2021), enfocados en el análisis de la presencia de las IEF en libros de texto de Educación Primaria, al abordarse solo dos y tres de las ideas propuestas por Batanero y Borovcnik (2016) y Burrill y Biehler (2011), respectivamente. A diferencia de estudios anteriores, enfocados en el currículo escolar o libros de texto, esta investigación se centra en los programas de estudio para la formación inicial del profesor de matemáticas de Educación Secundaria, lo que permitió identificar ausencias y fortalezas relacionadas con la presencia de las IEF.

Además, a la luz de esta investigación podemos resaltar la importancia de que los futuros profesores de matemáticas desarrollen las IEF durante su formación, con la finalidad de que ellos puedan desarrollarlas en sus estudiantes. En este punto sabemos que sí están presentes dichas IEF en los programas de estudio relacionados con estadística y probabilidad, lo que deja como futura línea de investigación indagar cómo es que se pueden desarrollar estas ideas de la mejor manera posible, logrando una comprensión y un razonamiento estadístico en el profesor, y cómo se pueden emplear las herramientas tecnológicas para favorecer su aprendizaje. Es decir, esta investigación no solo ofrece un diagnostico de la presencia de las IEF en la formación inicial del profesorado de matemáticas de Educación Secundaria, sino también ofrece elementos para repensar la incorporación de estas ideas en la preparación docente.

REFERENCIAS BIBLIOGRÁFICAS

Alsina, Á., Vásquez, C., Muñiz-Rodríguez, L. y Rodríguez-Muñiz, L. (2020). ¿Cómo promover la alfabetización estadística y probabilística en contexto? Estrategias y recursos a partir de la COVID-19 para Educación Primaria. Épsilon. Revista de la Sociedad Andaluza de Educación Matemática, 104, 99-128.

Batanero, C., Arteaga, P. y Contreras, J.M. (2011). El currículo de estadística en la enseñanza obligatoria. EM TEIA. Revista de Educação Matemática e Tecnológica Iberoamericana, 2(2), 1-20.

Batanero, C. y Borovcnik, M. (2016). Statistics and probability in high school. Sense Publishers.

Bernete, F. (2013). Análisis de contenido. En A. Lucas, y A. Noboa (Eds.), Conocer lo social: estrategias y técnicas de construcción y análisis de los datos (pp. 221-261). Editorial Fragua.

Bianchini, C. (2022). Propuesta didáctica que promueve el sentido estadístico centrada en ideas estocásticas fundamentales [Tesis doctoral, Universidad Nacional del Litoral].

Burrill, G., y Biehler, R. (2011). Fundamental statistical ideas in the school curriculum and in training teachers. En C. Batanero, G. Burrill y C. Reading (Eds.), Teaching Statistics in School Mathematics-Challenges for Teaching and Teacher Education: A Joint ICMI/IASE Study (pp. 57–69). Springer. https://doi.org/10.1007/978-94-007-1131-0_10

Cohen, L., Manion, L. y Morrison, K. (2002). Research methods in education. Routledge.

Dirección General de Educación Superior para Profesionales de la Educación [DGESPE] (2018). Planes de Estudio 2018. Licenciatura en Enseñanza y Aprendizaje de las Matemáticas en Educación Secundaria. DGESPE.

Estrella, S. (2017). Enseñar estadística para alfabetizar estadísticamente y desarrollar el razonamiento estadístico. En A. Salcedo (Ed.), Alternativas Pedagógicas para la Educación Matemática del Siglo XXI (pp. 173-194). Universidad Central de Venezuela.

Garfield, J. y Ben-Zvi, D. (2008). Developing students’ statistical reasoning: connecting research and teaching practice. Springer.

Heitele, D. (1975). An epistemological view on fundamental stochastic ideas. Educational Studies in Mathematics, 6(2), 187-205. https://doi.org/10.1007/BF00302543

Heymann, H.W. (2003). Why teach mathematics: A focus on general education. Kluwer Academic Publishers.

Inzunza, S., y Rocha, E. (2021). Los datos y el azar en el currículo de educación básica y bachillerato en México: reflexiones desde la perspectiva internacional. Diálogos sobre educación. Temas actuales en investigación educativa, 12(23), 1-13. https://doi.org/10.32870/dse.v0i23.717

Kilpatrick, J., Swafford, J. y Findell, B. (2001). Adding it up: Helping children learn mathematics. The National Academies Press. https://doi.org/10.17226/9822

Micheli, E. (2010). Desafíos y oportunidades en la enseñanza de la estadística. En U. Malaspina (Ed.), V Congreso Internacional sobre Enseñanza de las Matemáticas (pp. 3-18). Pontificia Universidad Católica del Perú.

Salcedo, A. (2019). Las ideas fundamentales de la estadística en textos escolares de matemáticas. En J.M. Contreras, M.M. Gea, M.M. López-Martín y E. Molina-Portillo (Eds.), Actas del Tercer Congreso Internacional Virtual de Educación Estadística (pp. 1-10). Universidad de Granada.

Salcedo, A., Uzcátegui, R. y Díaz-Levicoy, D. (2021). Ideas estadísticas fundamentales en libros de texto de matemáticas para la Educación Primaria en Nicaragua y Venezuela. IE Revista de Investigación Educativa de la REDIECH, 12, e1210. https://doi.org/10.33010/ie_rie_rediech.v12i0.1210

Secretaría de Educación Pública [SEP] (2018). Tratamiento de la Información. SEP.

Secretaría de Educación Pública [SEP] (2019). Pensamiento Estocástico. SEP.

Secretaría de Educación Pública [SEP] (2020). Estadística Inferencial. SEP.

Tauber, L., Cravero, M. y Santellán, S. (2019). La construcción del sentido estadístico a partir de indicadores sociales. En J.M. Contreras, M.M. Gea, M.M. López-Martín, y E. Molina-Portillo (Eds.), Actas del Tercer Congreso Internacional Virtual de Educación Estadística (pp. 1-9). Universidad de Granada.

Vásquez, C. y Cabrera, G. (2022). La estadística y la probabilidad en los currículos de matemáticas de educación infantil y primaria de seis países representativos en el campo. Educación Matemática, 34(2), 245-274. https://doi.org/10.24844/em3402.09

Verástegui, M., López-Flores, I. y García-García, J.I. (2023). Ideas estadísticas fundamentales en el programa de estudio de un curso de Estadística Inferencial para la formación inicial del profesor de matemáticas en México. En L. Tauber, C. Vásquez y J. Pinto-Sosa. (Eds.), Educación Estadística para la formación de ciudadanía crítica. Libro de ponencias de las Jornadas Latinoamericanas de investigación en Educación Estadística (pp. 92-99). Universidad Nacional del Litoral.

Watson, J.M. (2006). Statistical literacy at school: Growth and goals. Lawrence Erlbaum.

Zamora, J., Aguilar, E. y Guillén, H. (2022). Educación Estadística: tendencias para su enseñanza y aprendizaje en educación secundaria y terciaria. Revista Educación, 46(1), 547-567. https://doi.org/10.15517/revedu.v46i1.43494

Como citar:

Verástegui, M., López-Flores, J.I. y García-García, J.I. (2025). Ideas estadísticas fundamentales en la formación del profesor de matemáticas de Educación Secundaria en México. Revista de Educación Estadística, 4, 1-19. https://doi.org/10.29035/redes.4.1.8

Licencia de Creative Commons

Esta obra está bajo una licencia de Creative Commons
Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional.

1 * Autor de correspondencia: jaime.garcia@umce.cl (J.I. García-García)
https://orcid.org/0009-0003-4916-783X (mavg.1604@hotmail.com).
2 https://orcid.org/0000-0003-2350-2647 (jlopez@uaz.edu.mx).
3 https://orcid.org/0000-0002-8799-5981 (jaime.garcia@umce.cl).