Revista de Educación Estadística https://revistaeduest.ucm.cl/ Vol. 4, pp. 1-23, ene. 2025 - dic. 2025 ISSN 2810-6164

DOI: https://doi.org/10.29035/redes.4.1.11

 

EL CONOCIMIENTO PROBABILÍSTICO DE ESTUDIANTES PARA MAESTRO: DISEÑANDO Y ADAPTANDO PROBLEMAS DE PROBABILIDAD PARA ALUMNADO CON TRASTORNO DE ESPECTRO AUTISTA

Conhecimento probabilístico dos alunos para professores: concepção e adaptação de problemas de probabilidade para alunos com Perturbação do Espectro do Autismo

Prospective teachers’ probabilistic knowledge: designing and adapting probability problems for students with Autism Spectrum Disorder

 

Marlén Alonso-Castaño1

Universidad de Oviedo (Oviedo, España)

Carla Álvarez-Cándano2

Universidad de Oviedo (Oviedo, España)

Pablo Giadas3

Universidad de Oviedo (Oviedo, España)

 

Resumen

Los y las Estudiantes para Maestro (EPM) reciben una formación limitada en inclusión educativa dentro de los programas de formación inicial docente en matemáticas. Esta situación se acentúa durante la mención en educación especial, pues la formación en adaptaciones es general y no específica para matemáticas. En el caso de la probabilidad es esencial que los y las EPM adquieran habilidades para realizar adaptaciones adecuadas específicas de la materia. Así, en este estudio se diseñó una tarea formativa en la que 9 EPM de educación especial, con formación en probabilidad y resolución de problemas, debían crear y resolver un problema de probabilidad para 6.º de Educación Primaria y luego adaptarlo para una alumna con Trastorno de Espectro Autista y Trastorno Específico del Lenguaje. Se pretendía determinar cómo era el conocimiento matemático para la enseñanza mostrado por los y las EPM al desarrollar el problema con y sin adaptaciones. Para ello, se analizó su conocimiento matemático para la enseñanza a través de un análisis de contenido aplicando el modelo MTSK adaptado a probabilidad. Los resultados mostraron que ٨ de los y las ٩ EPM diseñaron problemas adecuados, pero sus adaptaciones fueron insuficientes, destacando la necesidad de mejorar su formación en adaptaciones específicas.

Palabras clave: probabilidad, enseñanza superior, formación de profesores, autismo, adaptación.

 

Resumo

Os estudantes do ensino superior (EES) recebem uma formação limitada em matéria de inclusão educativa no âmbito dos programas de formação inicial de professores de matemática. Esta situação é acentuada durante a especialização em educação especial, uma vez que a formação em adaptações não é específica da matemática. No caso da probabilidade, é essencial que os EES adquiram as competências necessárias para efetuar as adaptações adequadas às disciplinas específicas. Assim, neste estudo, foi concebida uma tarefa de treino em que 9 EES de educação especial, com formação em probabilidade e resolução de problemas, tiveram de criar e resolver um problema de probabilidade para o 6.º ano do Ensino Básico e depois adaptá-lo a um aluno com Perturbação do Espectro do Autismo e Perturbação Específica da Linguagem. O objetivo era determinar o conhecimento matemático para o ensino demonstrado pelos EES ao desenvolverem o problema com e sem adaptações. Para este efeito, o seu conhecimento matemático para o ensino foi analisado através do modelo MTSK adaptado à probabilidade. Os resultados mostraram que 8 dos 9 EES conceberam problemas adequados, mas as suas adaptações foram insuficientes, evidenciando a necessidade de melhorar a sua formação em adaptações específicas.

Palavras-chave: probabilidade, ensino superior, formação de professores, autismo, adaptação.

 

Abstract

Prospective teachers (PTs) receive limited training in educational inclusion within initial teacher education programmes in mathematics. This situation is accentuated during the specialisation in special education needs, as the training in adaptations is general and not specific to mathematics. In the case of probability, PTs must acquire the skills to make appropriate subject-specific adaptations. Thus, in this study, a training task was designed in which nine PTs specialising in special education needs, with training in probability and problem-solving, had to create and solve a probability problem for 6th grade of Primary School and then adapt it for a student with Autism Spectrum Disorder and Specific Language Disorder. The aim was to determine the mathematical knowledge for teaching shown by the PTs when designing the problem with and without adaptations. To this end, their mathematical knowledge for teaching was analysed through a content analysis applying the MTSK model adapted to probability. The results showed that 8 of the 9 PTs designed adequate problems, but their adaptations were insufficient, highlighting the need to improve their training in specific adaptations.

Keywords: probability, higher education, teacher training, autism, adaptation.

 

Recibido: 03/07/2025 - Aceptado: 15/07/2024

 

1. INTRODUCCIÓN

 

En la vida cotidiana, estamos constantemente expuestos a situaciones impredecibles y aleatorias, como el clima, el tráfico o el resultado de un sorteo. Estos fenómenos, caracterizados por su incertidumbre, nos han llevado a desarrollar herramientas matemáticas que permitan modelar, analizar y tomar decisiones informadas en contextos de azar. En este sentido, la probabilidad se ha convertido en un elemento clave dentro del currículo escolar, ya que proporciona al alumnado estrategias para interpretar situaciones de incertidumbre y aplicar el razonamiento probabilístico en su vida diaria (Alsina, 2016). Sin embargo, la enseñanza de la probabilidad presenta desafíos significativos. Estudios previos han señalado que el profesorado, tanto en formación como en ejercicio, suele tener dificultades en el dominio conceptual de la probabilidad, lo que repercute en su enseñanza (Alsina, 2016; Batanero, 2006; Batanero y Álvarez-Arroyo, 2024). En el caso del profesorado en formación, esta situación se agrava debido a la escasa formación específica de los contenidos probabilísticos y su didáctica dentro de los programas de educación matemática. Además, la formación en inclusión educativa dentro de estos programas suele ser general sin abordar específicamente la adaptación de contenidos matemáticos para alumnado con Necesidades Educativas Especiales (NEE). En particular, el alumnado con Trastorno de Espectro Autista (TEA) enfrenta barreras en el aprendizaje de la probabilidad debido a sus características cognitivas y comunicativas, que pueden afectar la comprensión de conceptos abstractos y la interpretación de enunciados matemáticos (Confederación Autismo España, 2021). Para garantizar una enseñanza inclusiva, es fundamental que el futuro profesorado desarrolle estrategias de adaptación que faciliten el acceso a los conceptos probabilísticos mediante el uso de representaciones visuales, manipulativos y lenguaje estructurado (Chico, Climent y Gómez-Hurtado, 2024; García-Moya et al., 2023).

Desde la didáctica de la matemática, el Mathematics Teachers’ Specialized Knowledge (MTSK) (Carrillo et al., 2013) se ha consolidado como un modelo para analizar el conocimiento especializado del profesorado en la enseñanza de las matemáticas. Su aplicación en el ámbito de la probabilidad ha dado lugar al Probabilistic Teachers’ Specialized Knowledge (PTSK) (Franco y Alsina, 2022), que permite evaluar el conocimiento didáctico y matemático del profesorado en relación con la probabilidad. A través de este modelo es posible examinar, no solo el dominio conceptual de la probabilidad por parte del futuro profesorado, sino también su capacidad para diseñar y adaptar problemas en función de las necesidades de su alumnado.

El presente estudio tiene como objetivo analizar el conocimiento matemático de un grupo de EPM cuando diseñan, resuelven y adaptan problemas de probabilidad en el contexto de alumnado con TEA y Trastorno Específico del Lenguaje (TEL). Para ello, se diseñó una actividad formativa en la que los y las EPM debían crear y resolver un problema de probabilidad para alumnado de 6.º de Educación Primaria para, posteriormente, adaptarlo para una alumna ficticia con TEA y TEL. A través del análisis de sus producciones, se ha buscado evaluar en qué medida el futuro profesorado aplica sus conocimientos de probabilidad y de educación inclusiva al desarrollar problemas matemáticos adaptados. Este estudio contribuye a la reflexión sobre la formación inicial del profesorado en la enseñanza de la probabilidad y la atención a la diversidad, con el fin de garantizar una educación inclusiva y de calidad.

 

2. MARCO TEÓRICO

 

El profesorado desempeña un papel fundamental en el proceso de enseñanza-aprendizaje, ya que su conocimiento y desempeño influyen directamente en la calidad educativa y en el desarrollo integral del alumnado. Por ello, resulta de gran interés analizar qué tipo de conocimiento posee el profesorado para la enseñanza de cada disciplina, pues este determinará, en gran medida, cómo se desarrollará el proceso de enseñanza-aprendizaje de su alumnado. En este contexto, Shulman (1986) revolucionó la forma en que se conceptualizaba el conocimiento docente al proponer su división en tres grandes dimensiones: el conocimiento del contenido, que hace referencia al dominio de la disciplina en sí misma; el conocimiento pedagógico del contenido, entendido como el saber específico que permite al docente enseñar dicho contenido de manera efectiva y el conocimiento curricular, relativo a la comprensión que el profesorado tiene sobre los programas y materiales que utilizan para enseñar abarcando cómo ese contenido está organizado, secuenciado y es presentado al alumnado. Esta propuesta tuvo un gran impacto en la investigación educativa originando diversas corrientes metodológicas de análisis del conocimiento del profesorado. En el ámbito de la educación matemática, Ball et al. (2008) ampliaron el enfoque de Shulman con el modelo Mathematical Knowledge for Teaching (MKT), que desglosa el conocimiento del profesorado en varios subdominios específicos que reflejan las competencias necesarias para enseñar matemáticas eficazmente. Este modelo distingue entre dos grandes áreas de conocimiento: el conocimiento del contenido matemático y el conocimiento pedagógico del contenido, cada uno desglosado en subdominios más detallados. Este modelo, no solo subraya la importancia de que el profesorado posea un conocimiento profundo de las matemáticas, sino también la habilidad para transformar ese conocimiento haciéndolo accesible para el alumnado. Los subdominios del MKT incluyen el conocimiento del contenido matemático, necesario para enseñar conceptos matemáticos particulares, y el conocimiento pedagógico, relacionado con cómo enseñar esos conceptos en distintos contextos y con diferentes tipos de alumnado. Esta distinción es esencial, ya que implica que, para ser eficaz, el profesorado no solo debe conocer las matemáticas en un nivel abstracto, sino también comprender cómo esos contenidos pueden ser enseñados y aprendidos, lo cual es especialmente relevante cuando se trata de alumnado con NEE. De este modo, el modelo MKT ofrece una visión integral de las competencias docentes que van más allá del dominio académico de las matemáticas, enfatizando la importancia de las estrategias pedagógicas para facilitar el aprendizaje. Posteriormente, Carrillo et al. (2013) refinaron esta propuesta con el modelo MTSK, delimitando con mayor precisión las áreas del conocimiento matemático especializado para la enseñanza (ver Figura 1).

 

Figura 1

Modelo de conocimiento MTSK.

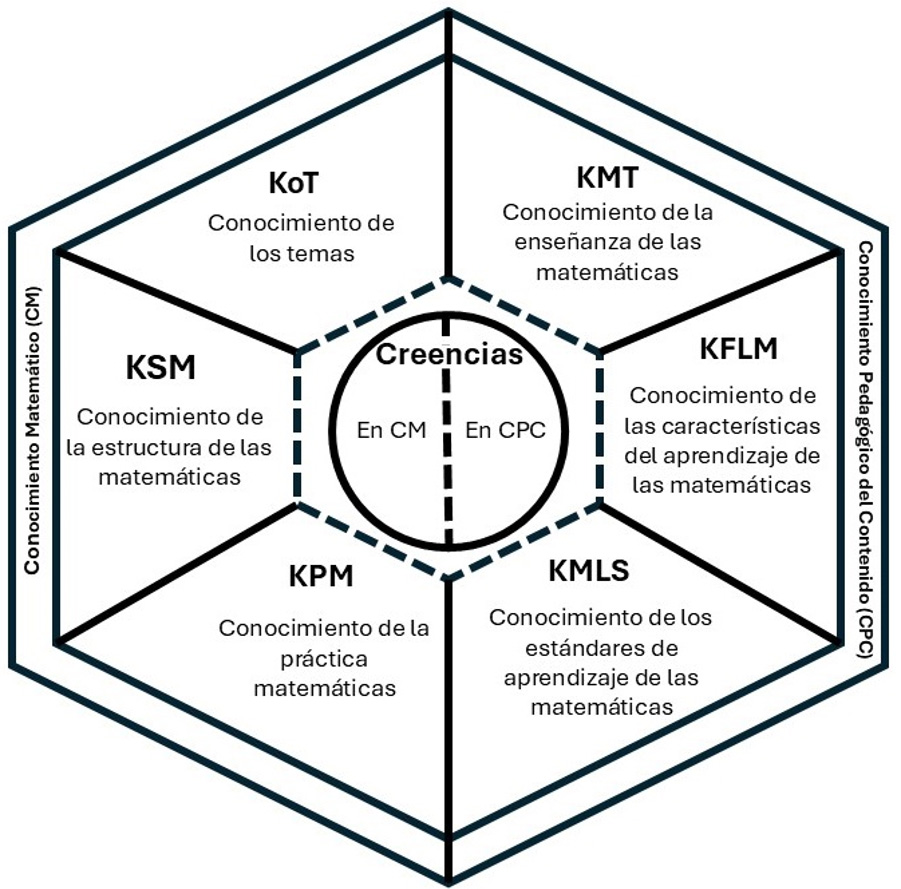
Nota. Adaptado de Carrillo et al. (2013).

 

El modelo MTSK profundiza en las dimensiones específicas del saber docente destacando la importancia de entender, no solo los conceptos matemáticos, sino también cómo presentarlos de manera efectiva, considerando el desarrollo cognitivo del alumnado y sus posibles dificultades. Este modelo subraya la interacción entre el conocimiento matemático y pedagógico, señalando que el profesorado debe integrar ambos para facilitar el aprendizaje lo que requiere, no solo un dominio de las matemáticas, sino también un conocimiento especializado en prácticas pedagógicas que favorezcan el aprendizaje en el aula. Asimismo, este modelo integra las creencias del profesorado, que permean todo el modelo, jugando un papel esencial, ya que influyen en la manera en que el profesorado interpreta y aplica su conocimiento especializado en el aula. Según este modelo, las creencias no solo afectan a las prácticas pedagógicas, sino que también condicionan el enfoque del profesorado sobre el contenido matemático y sobre cómo deben abordarlo en función de las características y necesidades del alumnado como también indican Estrada et al. (2003). En este sentido, resulta necesario que el profesorado sea consciente de sus propias creencias ya que estas pueden facilitar o limitar la aplicación efectiva de sus conocimientos especializados. Además, también afectan la manera en que se gestionan las dificultades cognitivas y emocionales que pueda experimentar el alumnado durante el aprendizaje matemático. La comprensión profunda del contenido y de las estrategias pedagógicas, junto con una reflexión crítica sobre las propias creencias, son esenciales para implementar un conocimiento especializado que sea verdaderamente transformador en el aula (Estrada et al., 2003).

Siguiendo esta línea, la formación del profesorado en estadística y probabilidad también ha sido objeto de estudio a través de adaptaciones del MTSK. La estocástica, que abarca tanto la probabilidad como la estadística, ha ganado importancia en los currículos escolares recientemente, a pesar de haber sido una disciplina poco tratada anteriormente (Alsina et al., 2020). La inclusión de estos contenidos busca proporcionar al alumnado las herramientas necesarias para recolectar, analizar e interpretar datos, habilidades fundamentales para tomar decisiones informadas (Alsina et al., 2020). Sin embargo, algunas investigaciones señalan que la enseñanza de estos temas enfrenta desafíos, principalmente debido a la formación insuficiente del profesorado en estocástica. En consecuencia, los modelos MTSK (Carrillo et al., 2013) y MKT (Ball et al., 2008) se han adaptado para centrarse en el conocimiento especializado necesario para enseñar estocástica en las escuelas. Así, Vidal-Szabó y Estrella (2019) desarrollaron el modelo Statistical Teachers’ Specialized Knowledge (STSK), aplicando el marco del MTSK a la enseñanza de la estadística. Por su parte, Franco y Alsina (2022) propusieron el modelo PTSK, adaptando el MTSK al conocimiento probabilístico y su aplicación didáctica, que será el que nos interese en este trabajo. Este modelo también divide el conocimiento en tres dominios principales: el conocimiento probabilístico (CP), el conocimiento didáctico de probabilidad (CDP) y las creencias. A continuación, se detallan los subdominios incluidos en el CP y el CDP.

Dentro del dominio del CP se incluyen los siguientes subdominios:

• Conocimiento de los Temas Probabilísticos (CTP): se centra en el conocimiento de los significados de la probabilidad, reglas, definiciones, aspectos fenomenológicos, diversos ejemplos, etc., aspectos que caracterizan y configuran este contenido. Por ejemplo, se diferencian diversos significados, reconociendo así el intuitivo, el frecuentista, el clásico o laplaciano (derivado de la regla de Laplace), el subjetivo y el axiomático.

• Conocimiento de la Estructura Probabilística (CEP): se trata del conocimiento sobre las distintas conexiones conceptuales, de las cuales el docente debe establecer relaciones o vínculos basados en conocimientos probabilísticos elementales, pero también en el cálculo de probabilidades, la cuantificación de la posibilidad de ocurrencia de eventos, etc.

• Conocimiento de la Práctica de la Probabilidad (CPP): es el subdominio que abarca las diferentes maneras de conocer, crear y/o producir probabilidad. En este sentido, es importante considerar que la probabilidad está relacionada con la capacidad de participar en la vida cotidiana en situaciones de incertidumbre. Según Gal (2005), se diferencian tres características para manejar la probabilidad en la vida real: la participación del individuo, la gestión de la incertidumbre y el manejo del riesgo. Además, parece esencial destacar el uso de contextos reales, significativos y motivadores para el alumnado (Alsina et al., 2020).

Por su parte, dentro del dominio del CDP se incluyen los siguientes subdominios:

• Conocimiento de la Enseñanza de la Probabilidad (CENP): este subdominio abarca el conocimiento del profesorado sobre las estrategias para fomentar el desarrollo adecuado de las habilidades probabilísticas y ayudar al alumnado a desarrollar su conocimiento sobre probabilidad. Por ello, se incluyen estrategias, recursos y materiales para facilitar su comprensión. El profesorado debe proporcionar experiencias para observar fenómenos aleatorios organizando correcta y claramente la recogida de datos, de modo que el alumnado pueda contrastar resultados y hacer predicciones. Además, es importante resaltar la imprevisibilidad y variabilidad, ayudándoles a apreciar los fenómenos a través de la acumulación de resultados.

• Conocimiento de las Características de Aprendizaje de la Probabilidad (CCAP): se refiere al conocimiento de las características y procesos de comprensión del alumnado hacia los distintos contenidos relacionados con la probabilidad, así como el lenguaje, las posibles dificultades y errores, los aspectos que consideran más accesibles y sencillos, etc. El docente debe ser consciente de los diferentes errores que pueden surgir en relación con la probabilidad para actuar como guía en el aprendizaje y resolución de los problemas que surjan en el aula.

• Conocimiento de los Estándares de Aprendizaje de la Probabilidad (CEAP): se centra en el conocimiento de los contenidos probabilísticos que deben ser enseñados y aplicados según las normativas educativas. Según la legislación educativa vigente (Ministerio de Educación y Formación Profesional, 2022), la probabilidad empieza a trabajarse en el segundo ciclo desde los significados intuitivo y subjetivo siendo, en el tercer ciclo, donde se comienza a aplicar el cálculo de probabilidades en experimentos, comparaciones o investigaciones, a partir de la definición clásica de probabilidad, con ejercicios y problemas que se resuelven utilizando la regla de Laplace, o a partir de la definición frecuencial de la probabilidad, mediante experimentos con un elevado número de repeticiones. Como podemos observar, entre estos ciclos se trabajan todos los significados de la probabilidad, salvo el axiomático que, por su complejidad cognitiva, aún no se puede introducir en Educación Primaria (Alsina y Vásquez, 2016).

Finalmente, las creencias se consideran en el mismo sentido que en el modelo MTSK, pero se centran en el ámbito de la probabilidad y su didáctica. El esquema del modelo PTSK se muestra en la Figura 2.

 

Figura 2

Modelo de conocimiento PTSK.

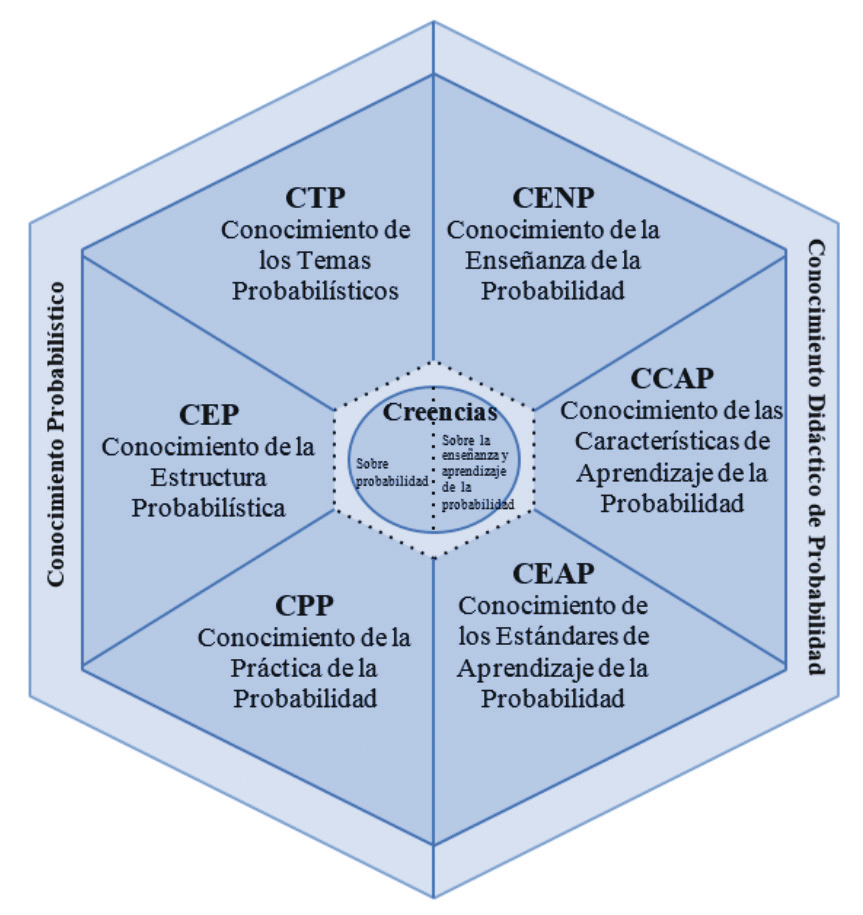
Nota. Tomado de Franco y Alsina (2022, p. 85).

 

Así, podemos ver que el conocimiento especializado del profesorado en el ámbito de la probabilidad resulta ser un componente esencial en la enseñanza de las matemáticas, pues permite estructurar y adaptar los contenidos para garantizar un aprendizaje significativo. En este sentido, es fundamental considerar cómo estos conocimientos pueden aplicarse en contextos inclusivos, asegurando que todo el alumnado, incluyendo aquel con NEE, tenga acceso a un aprendizaje adaptado a sus características y necesidades. La clasificación de alumnado con NEE y Necesidades Específicas de Apoyo Educativo (NEAE) abarca a un amplio grupo de estudiantes con características diversas. Según Booth et al. (2002), estas adaptaciones deben seleccionarse según las necesidades de cada estudiante para minimizar las barreras al aprendizaje. En este sentido, las adaptaciones se definen como cambios realizados en la escuela que promueven el acceso al aprendizaje, modificando la forma en que este se lleva a cabo y eliminando obstáculos (Lee, 2024). De acuerdo con la Confederación Autismo España (2021), uno de cada cuatro estudiantes con NEE tiene TEA. La mayoría de estos y estas estudiantes siguen escolarización ordinaria, lo que plantea numerosos desafíos para su inclusión y la promoción de una educación de calidad. Es fundamental subrayar la necesidad de adaptar la educación, no solo a este grupo de estudiantes, sino también a los distintos casos individuales de NEE y NEAE que se presentan en las aulas, con el fin de atender a la diversidad, tal como lo establece la legislación educativa vigente en España (Ministerio de Educación y Formación Profesional, 2022). En este sentido, la planificación docente juega un papel clave en la implementación de adaptaciones curriculares efectivas, no solo para estudiantes con discapacidad, sino también para aquellos con NEE no asociadas a una discapacidad, como señalan Barrera-Proaño et al. (2024). Por tanto, el profesorado debe considerar que no todo el alumnado aprende de la misma manera, planificando las actividades y adaptaciones necesarias para ofrecer una educación inclusiva en la que se involucren en el aprendizaje y no se sientan excluidos.

En cuanto a las matemáticas, el alumnado con TEA parece tener dificultades relacionadas con el procesamiento de la información, las funciones ejecutivas y las diferencias en el procesamiento simbólico, entre otros aspectos (Chico, Climent y Gómez-Hurtado, 2024; Chico, Polo-Blanco et al., 2024). Hasta ahora, se han realizado trabajos como el de García-Moya et al. (2023) en el que se aborda el pensamiento probabilístico en estudiantes de secundaria con TEA mostrando las fortalezas y debilidades que este tipo de alumnado presenta en cuanto a la probabilidad y su aplicación en la vida cotidiana. Este trabajo, indica que el alumnado participante presenta dificultades en la comprensión y atención, aunque se confirma el conocimiento de términos y expresiones probabilísticas en contextos cotidianos. Esto implica que el foco de los trabajos relativos a adaptaciones ha sido su aplicación al alumnado según sus características, pero no existen trabajos previos centrados en el conocimiento del profesorado que imparte la materia sobre cómo realizar estas adaptaciones en probabilidad, qué aspectos deben tener en cuenta, su importancia, etc., como ocurre en este trabajo, lo que supone una novedad en el campo. Por lo tanto, es un desafío y es necesario centrar esfuerzos en formar y sensibilizar al futuro profesorado para que implemente metodologías y desarrolle adaptaciones adecuadas que favorezcan la inclusión y eviten la exclusión (Palacios-García, 2024). En este sentido, este trabajo permite obtener resultados preliminares sobre el conocimiento que tiene el futuro profesorado respecto a las adaptaciones educativas en el ámbito de la probabilidad, a partir del modelo PTSK (Franco y Alsina, 2022), así como determinar en qué áreas debe centrarse la formación, lo que posibilitará una mejora en los programas de formación docente.

 

3. MÉTODO

 

Esta investigación presenta un estudio exploratorio sobre cómo es el conocimiento de los y las EPM a la hora de hacer adaptaciones curriculares para alumnado con TEA y TEL en el ámbito de la probabilidad. Así, en esta sección se presenta el diseño del trabajo mostrando los y las EPM, el instrumento para la recogida de datos y la metodología empleada en el estudio.

 

3.1. Población y muestra

 

Para este estudio se tomó una muestra inicial de 44 EPM de tercer curso del Grado en Maestro/a de Educación Primaria de la Universidad de Oviedo, en la asignatura Matemáticas y su Didáctica III, versada en estadística, probabilidad y resolución de problemas y su didáctica. Posteriormente, se filtró la muestra por especialidades, seleccionando a los y las nueve EPM que cursaban la mención en educación especial, con el fin de analizar su conocimiento sobre la enseñanza de la probabilidad y las adaptaciones curriculares. Los y las nueve EPM (siete mujeres y dos hombres), de entre ٢٠ y ٥٠ años, cursaban la asignatura por primera vez. La mayoría accedió a la titulación a través de la EBAU, aunque tres lo hicieron mediante vías para mayores de ٢٥ y ٤٠ años, con formaciones previas en áreas como Biología, Relaciones Públicas y Promoción de Igualdad de Género.

 

3.2. Instrumento

 

El instrumento de este estudio es una tarea formativa no evaluable de la asignatura Matemáticas y su Didáctica III. Esta tarea constaba de tres apartados, que fueron proporcionados a los y las EPM de manera secuenciada. Es decir, los y las EPM no sabían qué deberían realizar en el siguiente apartado. A continuación, se muestran dichos apartados.

El primer apartado consistió en el diseño y resolución de un problema de probabilidad dirigido al alumnado de 6.º curso de Educación Primaria. La resolución debía adecuarse a este nivel educativo e incluir una representación gráfica. Posteriormente, debían responder a una serie de preguntas sobre el diseño y resolución del problema, abordando las dificultades del alumnado, estrategias para superarlas y la razón de su elección según el nivel educativo. El enunciado de esta parte de la tarea es el siguiente:

 

PRIMERA PARTE

Diseña y resuelve un problema de probabilidad dirigido al 6º curso de Educación Primaria. El problema deberá de ser resuelto como lo haría un niño de esta etapa, incluyendo una representación gráfica. A continuación, responde a las siguientes preguntas, justificando tus respuestas.

1. ¿Qué dificultades crees que se puede encontrar un niño de ese curso al enfrentarse a este problema?

2. ¿Cómo puedes ayudarle a afrontar esas dificultades?

3. ¿Por qué has elegido este problema? Justifica tu elección y la adecuación del problema al nivel educativo.

Para dicho apartado, se esperaba que se aplicase el significado frecuencial de la probabilidad, basado en la idea de que la probabilidad de un evento se obtiene a partir de la frecuencia relativa de su aparición en un número elevado de repeticiones de un experimento aleatorio; o el significado clásico de la probabilidad, pudiendo resolver el problema mediante la regla de Laplace. Es decir, si realizamos un experimento aleatorio cuyo espacio muestral sea finito, con n sucesos elementales, todos ellos equiprobables, la probabilidad de que ocurra el suceso sería el cociente resultante de la división:

P(A)= (número de casos favorables)/(número de casos posibles)

 

Esta suposición se debe a que, a pesar de que podrían trabajarse otros significados de la probabilidad con alumnado de 6.º de Educación Primaria, dichos conocimientos ya se han adquirido en cursos previos, por lo que, basándonos en los contenidos del currículo de Educación Primaria para este nivel, deberían trabajarse los significados frecuencial y/o clásico. Estos significados no pueden trabajarse en niveles previos debido a su complejidad cognitiva para alumnado de cursos inferiores.

En el segundo apartado, a partir de lo realizado en el primero, se planteó un caso concreto ficticio sobre una niña del mismo curso con TEA y TEL. A partir de este caso, se solicitó a los y las EPM que adaptasen el problema diseñado y resuelto en el primer apartado. En este caso, deberían tener en cuenta las características típicas de este alumnado, adaptando el enunciado y/o resolución, con el fin de que la estudiante pudiese adquirir las nociones básicas de probabilidad adaptadas a sus necesidades. Hemos optado por un doble diagnóstico debido a la habitual comorbilidad de ambos trastornos, lo que justifica la necesidad de apoyos visuales y representaciones gráficas para facilitar la comprensión y el procesamiento de la información por parte de este alumnado. Cabe destacar la importancia de que los y las EPM no conociesen previamente la naturaleza de este segundo apartado, de modo que evitásemos una simplificación excesiva del primer problema diseñado, así como ofrecerles una guía para que el problema fuese más sencillo de adaptar. El segundo apartado del instrumento es el siguiente:

 

SEGUNDA PARTE

Lee atentamente la siguiente situación:

CASO DE INTERVENCIÓN PROPUESTO PARA REALIZAR LA ADAPTACIÓN

Nombre: Mara.

Edad: 11 años.

Curso: 6.º de Educación Primaria.

Diagnóstico: TEA, TEL (Trastorno Específico del Lenguaje).

Caso para la intervención: Mara es una niña de 11 años, escolarizada según la modalidad ordinaria en un centro público. Esta niña muestra dificultades en las matemáticas a la hora de comprender conceptos abstractos, al igual que cuando se le plantean problemas complejos. Necesita mucho apoyo visual, y estaría a nivel del 1.º o 2.º curso de esta etapa educativa.

No solo padece TEA, sino que también tiene TEL, lo cual dificulta la adquisición matemática y su expresión al hablar. Sus dificultades más concretas en esta área son en conceptos más complejos, como las fracciones, y la probabilidad y estadística. Su rendimiento es bajo y pobre en cuanto a las matemáticas, se distrae en cuanto hay mucho ruido de fondo y se desconcentra con facilidad cuando está haciendo la tarea.

Teniendo en cuenta la situación anterior, supón que esta alumna se encuentra en la misma clase de 6.º de Educación Primaria para la que has planteado el problema de la primera parte de este estudio.

Realiza una modificación de tu enunciado y/o de tu resolución anteriores de manera que el problema se encuentre adaptado a las necesidades de la alumna, con el fin de que pueda adquirir las nociones básicas de probabilidad que se trabajan en el problema. A continuación, responde a las siguientes preguntas, justificando tus respuestas.

1. ¿Qué dificultades crees que se puede encontrar Mara al enfrentarse a este problema?

2. ¿Cómo puedes ayudarla a afrontar esas dificultades?

3. ¿Por qué has modificado el problema y/o la resolución de esta forma? Justifica tu respuesta de manera razonada.

Nota: Ten en cuenta que el TEA (Trastorno de Espectro Autista) es un trastorno neurobiológico del desarrollo que se manifiesta en los primeros años de vida, siendo permanente, es decir, perdura a lo largo de toda la vida, y que presenta síntomas diversos, como deficiencias en la comunicación y en las interacciones sociales, y patrones restrictivos y repetitivos de comportamiento e intereses.

 

En este apartado, se esperaba que los y las EPM identificasen las necesidades de adaptación del problema para la alumna, teniendo en cuenta que el TEA es un trastorno neurobiológico que aparece antes de los 6 años y persiste toda la vida, caracterizándose por dificultades en la interacción social, la comunicación y patrones de comportamiento repetitivos. Asimismo, debían considerar que el TEL es un trastorno del desarrollo del lenguaje que afecta tanto la expresión como la comprensión, dificultando la adquisición de habilidades lingüísticas sin estar asociado a una discapacidad. De este modo, se pretendía que fuesen capaces de adaptar el problema pasando a preguntar por un significado intuitivo, adaptado al nivel en el que se encontraba la alumna, simplificando las preguntas y/o la resolución, añadiendo elementos visuales como dibujos o pictogramas, o trabajando con materiales manipulativos, entre otras posibilidades. Teniendo en cuenta que la alumna se encuentra a nivel del primer ciclo de Educación Primaria, ciclo en el que actualmente no se contempla el estudio de la probabilidad, lo más natural sería trabajar con ella desde un enfoque intuitivo, que es el significado más sencillo y sobre el que se comienza a trabajar sobre los contenidos de probabilidad.

En el tercer apartado, se incluyó un cuestionario de opinión para conocer las creencias y dificultades de los y las participantes sobre la enseñanza de la probabilidad, que se muestra a continuación:

 

TERCERA PARTE

Una vez realizadas ambas partes de la propuesta, contesta a las siguientes preguntas de manera justificada:

1. ¿Cómo explicarías al alumnado lo que es la probabilidad?

2. ¿Consideras que tus conocimientos matemáticos sobre probabilidad son suficientes para enfrentarte a una clase de este contenido en educación primaria? En caso afirmativo, justifica por qué. En caso negativo, ¿qué cambiarías o crees que te falta para mejorarlos?

3. ¿Cuál crees que ha sido tu mayor dificultad a la hora de realizar el problema SIN adaptar?

4. ¿Cuál crees que ha sido tu mayor dificultad a la hora de ADAPTAR el problema?

 

A pesar de haber recogido esta información, su análisis no se ha incorporado en este trabajo, ya que no forma parte del objetivo del estudio, centrado en el conocimiento matemático al diseñar, resolver y adaptar problemas en contextos de TEA y TEL. Además, los resultados obtenidos fueron limitados y no permitieron una integración clara en marcos teóricos consolidados.

 

3.3. Análisis de contenido

 

Para el análisis de los datos se llevó a cabo un análisis de contenido, una metodología de investigación descriptiva que permite clasificar la información en categorías cuantificables (Raigada, 2002). Los problemas planteados por los y las EPM se clasificaron en 3 categorías distintas en función de la adecuación de su planteamiento y su resolución:

• Correctos: problemas adecuadamente diseñados para el nivel de 6.º de Educación Primaria, correctamente resueltos, con representación gráfica clara y justificaciones de los pasos dados.

• Parcialmente correctos: problemas cuyo diseño era adecuado, pero que presentaban errores menores en la redacción o pequeños fallos en la resolución, con justificaciones parciales.

• Incorrectos: problemas no adecuados para el nivel de 6.º de Educación Primaria con errores en la resolución, sin representación gráfica y sin justificaciones.

A continuación, mediante el modelo PTSK (Franco y Alsina, 2022), se examinó el diseño y la adaptación de cada problema para evaluar el conocimiento matemático en la enseñanza de la probabilidad y sus adaptaciones curriculares. Este análisis se centró en cinco subdominios del modelo PTSK.

• CTP: se evaluó si los y las EPM comprendían los significados de probabilidad que resultaban adecuados para el nivel educativo del problema, en este caso, el enfoque clásico basado en la regla de Laplace o el frecuencial basado en las frecuencias relativas. Además, se analizó su capacidad para formular un problema que requiriese de la aplicación de la regla de Laplace o de las frecuencias relativas.

• CEP: se analizó este subdominio en función de los vínculos y relaciones con otros conceptos matemáticos, evitando limitarse exclusivamente a la probabilidad. En este contexto, podían abordarse aspectos como la representación de fracciones, números decimales y porcentajes.

• CCAP: respecto a este subdominio, se analizó el planteamiento y la justificación de las dificultades que puede enfrentar el alumnado de ٦.º de Educación Primaria, así como los posibles errores vinculados a la forma, los métodos y las características del proceso de aprendizaje del alumnado respecto a la probabilidad en esta etapa educativa.

• CENP: se analizó si los y las EPM eran capaces de plantear recursos, materiales y estrategias de resolución diferentes con el fin de facilitar el acceso a las nociones de probabilidad evitando errores y dificultades en el alumnado.

• CEAP: se analizó si los y las EPM conocían la legislación vigente con respecto al Bloque E. Sentido Estocástico (dentro de los saberes básicos de Matemáticas), tanto en la etapa del segundo ciclo como del tercero.

Para analizar los resultados del primer apartado, se utilizaron los subdominios CTP, CEP y CEAP, con el objetivo de evaluar el diseño y resolución del problema dirigido a estudiantes de 6.º de Educación Primaria, considerando que ya tenían conocimientos sobre la probabilidad, sus condiciones, su significado, etc. Asimismo, debían emplear el significado de probabilidad adecuado para el nivel educativo solicitado. Esto permite identificar el conocimiento que poseen ante posibles errores y dificultades que el alumnado puede encontrar y, por ende, facilitar recursos o alternativas para mejorar la comprensión por su parte.

En el segundo apartado, centrado en la adaptación del problema para la alumna ficticia con TEA y TEL, se tomaron en cuenta los subdominios CENP, CCAP y CEAP. Aquí, los y las EPM debían adaptar el problema considerando las necesidades de la estudiante y proponiendo estrategias de apoyo, considerando un nivel más bajo al del resto del alumnado.

La codificación fue realizada de forma independiente por los tres investigadores, comparando y discutiendo luego las discrepancias hasta alcanzar consenso, lo que reforzó la validez del análisis mediante triangulación.

 

4. RESULTADOS

 

En este apartado se muestran los resultados obtenidos a través del análisis del contenido durante el diseño y resolución de problemas probabilísticos no adaptados y adaptados de los y las EPM sobre su desempeño y su conocimiento para la enseñanza de la probabilidad.

En la Tabla 1 se encuentra una síntesis de los resultados relativos al análisis del contenido y de los subdominios del PTSK. Dentro de los subdominios se han identificado tanto evidencias como indicios. Se consideran evidencias aquellas manifestaciones explícitas en las respuestas que permiten reconocer de manera directa la presencia de un conocimiento. En cambio, los indicios son manifestaciones implícitas que sugieren la existencia de un conocimiento, aunque este no se mencione de forma explícita.

Por ejemplo, si un o una EPM afirma que su problema está adaptado al nivel educativo porque en el currículo de Educación Primaria se trabaja un determinado contenido, proporciona una evidencia de su conocimiento del currículo. En cambio, si la adaptación es adecuada, pero no se hace referencia explícita al currículo, se considera que muestra indicios de dicho conocimiento. Además, se han identificado el tipo de problema, el significado de la probabilidad empleado y los tipos de adaptaciones realizados por cada EPM (en caso de haberlos).

 

Tabla 1

Síntesis de los resultados presentados por los y las EPM

EPM	Clasificación cualitativa	Tipo de problema	Significado de la probabilidad	Adaptación del problema	Subdominios del PTSK
1	Parcialmente correcto	Lanzamiento de un dado	Clásico	No hay modificación	Evidencias: CTP, CENP, CCAP y CEP
2	Parcialmente correcto	Bolas de colores	Clásico	Modificación con dibujos	Evidencias: CTP; Indicios: CEAP y CENP
3	Parcialmente correcto	Bolas de colores	Clásico	Modificación mediante simplificación del enunciado, pero con un error en el recuento de bolas	Indicios: CTP y CEAP; Evidencias: CCAP y CENP
4	Correcto	Lanzar una moneda y un dado (2 eventos)	Clásico	No hay modificación	Indicios: CTP y CEAP; Evidencias: CCAP y CENP
5	Correcto	Caramelos	Clásico	No hay modificación, pero propone la búsqueda de un tema de interés para la alumna	Indicios: CTP y CEAP; Evidencias: CEP, CCAP y CENP
6	Correcto	Canicas de colores	Clásico	Modificación mediante pictogramas	Indicios: CTP, CEAP y CEP; Evidencias: CCAP y CENP.
7	Incorrecto	Estudiantes con asignaturas aprobadas	Clásico	No hay modificación	Evidencias de falta de conocimientos.
8	Correcto	Bolas de colores	Clásico	Modificación mediante simplificación de enunciado y preguntas	Indicios: CTP, CEAP, CCAP y CENP
9	Correcto	Lanzamiento de un dado (temática medieval)	Intuitivo	No hay modificación	Evidencias: CTP, CCAP, CENP, CEAP y posible combinación de CEP y CCAP

Nota. Elaboración propia.

 

Se identificaron cinco problemas correctos, tres parcialmente correctos y uno incorrecto. Se observó que todos los y las EPM coincidían en proponer enunciados sencillos con elementos prototípicos, como el lanzamiento de monedas, de dados o la extracción de bolas de colores o caramelos de urnas o bolsas para trabajar la probabilidad, empleando números pequeños. La única excepción fue el EPM7 que presentó un problema más complejo, con números grandes y un contexto menos común. Curiosamente, este EPM fue el único que planteó un problema que resultó incorrecto presentando múltiples errores en el planteamiento y la resolución (ver Figura 3).

Podemos observar que el problema presenta unos números muy elevados para el cálculo de probabilidades en este nivel educativo no resultando adecuado para un curso de 6.º de Educación Primaria. Además, los datos proporcionados podrían ser insuficientes para que el alumnado resuelva el problema. Todo ello evidencia una falta de CTP y CEAP. Se podría haber utilizado una tabla de contingencia para llegar a la solución, pero esta representación gráfica no aparece. El único apartado correcto es el tercero, ya que aparece directamente en el enunciado.

 

Figura 3

Problema propuesto por el EPM7

 

El resto de los problemas que presentan algún error (EPM1, EPM2 y EPM3) y que, por tanto, se clasificaron como parcialmente correctos, muestran errores de tipo conceptual, como multiplicar por 100 la fórmula de la regla de Laplace para expresar el resultado en forma de porcentaje, ambigüedades en el enunciado, que no permiten determinar si hay reposición o no tras la extracción de una bola y errores de conteo. Este tipo de errores son habituales en la literatura (Alonso-Castaño, 2021), mostrando falta de CTP por parte de los y las EPM. En cuanto al significado de la probabilidad utilizado, se observó que la mayoría de los y las EPM (ocho de los nueve) aplicaron el significado clásico de probabilidad, debiendo resolver el problema mediante la regla de Laplace, lo que sugiere un buen CEAP por parte de la mayoría de los y las EPM. Sin embargo, uno de los y las participantes recurrió a un enfoque intuitivo, lo que refleja posibles carencias en su CEAP. El EPM9, a pesar de proponer un problema matemáticamente correcto, lo dirigió a un nivel más bajo al trabajar ese enfoque de la probabilidad.

Por otra parte, en el apartado de adaptación, solo cuatro EPM realizaron modificaciones a los problemas según se les había solicitado, mientras que el resto propusieron soluciones alternativas sobre cómo trabajar con la alumna ficticia en esa situación o simplemente respondieron las preguntas planteadas, pero sin hacer ningún tipo de modificación en el problema. Los y las EPM que realizaron modificaciones (EPM2, EPM3, EPM6 y EPM8) introdujeron estrategias como la inclusión de dibujos, pictogramas y materiales manipulativos, así como la reformulación y simplificación de los enunciados para facilitar la comprensión del problema. Por ejemplo, el EPM8 propuso preguntar solo por una extracción en lugar de dos, reduciendo la carga verbal y ajustando el nivel de complejidad. Estas adaptaciones evidencian CENP al incorporar apoyos visuales y CCAP al reconocer la necesidad de ajustar el nivel de la actividad a las características de la estudiante con TEA y TEL. No obstante, en general, las modificaciones resultaron insuficientes, ya que algunas fueron superficiales o no lograron adecuarse plenamente al nivel de desarrollo cognitivo y lingüístico de la alumna ficticia. Esto indica que, aunque existen ciertas evidencias de estos subdominios, la adquisición de conocimiento por parte de los y las EPM aún requiere de una mayor consolidación, lo que supone un margen de mejora en la aplicación efectiva de estas estrategias. Por su parte, la mayoría de los y las EPM que no realizaron modificaciones en sus problemas (EPM1, EPM4, EPM5 y EPM9) sugirieron realizar adaptaciones en la metodología empleada con la alumna ficticia. Estas adaptaciones contemplaban la inclusión de materiales manipulativos, de elementos visuales como dibujos o pictogramas, la división del problema en varios apartados que hiciesen a la alumna resolver la tarea paso a paso para no abrumarla con un enunciado con demasiadas preguntas o tareas, o el rediseño del contexto de la tarea para buscar una temática que resultase de interés para la alumna. El EPM9 también propone un cambio físico de lugar en el aula para evitar distracciones. Esto muestra evidencias de CENP por parte de los y las EPM, ya que han identificado adecuadamente materiales y recursos válidos para la adaptación de esta estudiante. Sin embargo, aunque estas medidas pueden ser adecuadas para un caso como el de esta alumna, aún resultan insuficientes ya que su desarrollo cognitivo no le permitirá resolver un problema mediante la definición clásica de la probabilidad, lo que muestra falta de CCAP por parte de estos EPM. Asimismo, como estas medidas no consiguen una adaptación adecuada al nivel, también se muestra una falta de CEAP, ya que, por lo general, estos EPM no identifican que el significado que deben trabajar con la alumna es el intuitivo. Cabe destacar que el EPM9, que inicialmente propuso un problema en el que se trabajaba la probabilidad de manera intuitiva al hablar de “posibilidades” y no de “probabilidades”, ahora indica que debería hablarse de “posibilidades” a la alumna con TEA y TEL y no de “probabilidades”. Esto sugiere que es posible que inicialmente quisiese trabajar con un significado clásico de la probabilidad, pero que no posea suficiente CTP para hacerlo y haya mezclado conceptos. Sin embargo, sí sabe identificar que la alumna del caso ficticio debería trabajar con la probabilidad intuitiva, por lo que muestra evidencias de CEAP, siendo el único EPM que indica el tipo de adaptación que resultaría adecuada. Por su parte el EPM7 no es capaz de indicar ningún tipo de adaptación adecuada al problema. Introduce una tabla con la que indica que la alumna “podrá verlo de una forma visual”, pero esa tabla no facilita la adaptación del problema en ningún aspecto. Por tanto, muestra falta de CCAP, CENP y CEAP.

 

5. DISCUSIÓN Y CONCLUSIONES

 

El objetivo principal de este estudio fue analizar el conocimiento probabilístico de un grupo de EPM centrándose en cómo aplicaban sus conocimientos en probabilidad y su comprensión de la educación inclusiva al crear y adaptar problemas de probabilidad para una alumna ficticia de 6.º de Educación Primaria con TEA y TEL. A partir del análisis de sus producciones se ha logrado identificar varios aspectos clave relacionados con la formación en probabilidad y la atención a la diversidad. Se observa una tendencia general a usar el enfoque clásico de probabilidad, aunque varía su adecuación al nivel educativo. Las diferencias principales radican en la profundidad de las adaptaciones y en la correcta identificación del significado adecuado para la alumna ficticia, reflejando distintos niveles en los subdominios del PTSK. Los resultados obtenidos muestran que la mayoría de los y las EPM cuentan con un conocimiento adecuado de la probabilidad para la docencia en 6.º de Educación Primaria. Ocho de nueve EPM consiguieron crear y resolver problemas dentro del nivel esperado para esta etapa educativa, lo que refleja un buen dominio de los contenidos, del currículo y una adecuada aplicación del significado clásico de probabilidad como ya ocurría en Alonso-Castaño (2021). Sin embargo, cuando se les pidió realizar adaptaciones para una alumna con TEA y TEL, mostraron dificultades significativas, como también ocurre en Barrera-Proaño et al. (2024) que indican que gran parte del profesorado carece de la capacitación necesaria para desarrollar adaptaciones curriculares adecuadas para estudiantes con NEE, lo que afecta negativamente a su desempeño académico. A pesar de que reconocieron la necesidad de trabajar con recursos visuales y manipulativos, sus adaptaciones fueron insuficientes. Este hallazgo refleja una brecha en la formación específica sobre la atención a la diversidad dentro del área de la probabilidad, ya que no lograron realizar modificaciones que permitieran trabajar con la probabilidad de forma intuitiva y accesible para la alumna. En este sentido, estudios como Palacios-García (2024) enfatizan la necesidad de que el profesorado reciba formación específica sobre adaptaciones curriculares efectivas, pues la falta de preparación puede limitar la inclusión de este alumnado. Además, si bien los y las EPM reconocieron la importancia de adaptar los problemas a las necesidades del alumnado, las soluciones propuestas no fueron suficientes: aunque los recursos visuales y manipulativos fueron identificados correctamente como útiles para la adaptación, los y las EPM no supieron integrarlos de manera efectiva en los problemas de probabilidad. En particular, al adaptar el contenido para la alumna ficticia con TEA y TEL, los y las EPM no lograron ajustar el nivel de complejidad o proporcionar una experiencia de aprendizaje que se alineara con el enfoque de probabilidad intuitiva necesario para esta alumna. Esto resalta una debilidad significativa en la formación recibida ya que no pudieron identificar adecuadamente las dificultades específicas de aprendizaje asociadas con estos trastornos, lo que limita su capacidad para ofrecer una educación inclusiva efectiva. Según Chico, Climent y Gómez-Hurtado (2024), para que la adaptación curricular sea efectiva en el caso de estudiantes con TEA, es esencial incorporar materiales visuales y manipulativos ajustando la metodología de enseñanza de acuerdo con las características cognitivas y sociales de este alumnado, adaptando los contenidos a las necesidades de cada estudiante, lo que ha sido una limitación en la formación de los y las EPM en este estudio. Para este alumnado, se recomienda usar apoyos visuales, como pictogramas; materiales manipulativos, como bolsas de objetos, y enunciados claros y secuenciados. En el alumnado con TEL, se debe reforzar el vocabulario específico con imágenes y ejemplos cotidianos, además de usar apoyos visuales. Estas adaptaciones hacen accesible el aprendizaje de la probabilidad proporcionando al futuro profesorado herramientas prácticas para atender la diversidad de manera inclusiva y rigurosa. Por otra parte, los resultados indican que, aunque los y las EPM están recibiendo formación en educación especial, aún no cuentan con las competencias necesarias para realizar adaptaciones específicas en disciplinas como matemáticas y, en este caso, probabilidad. La formación ofrecida en las asignaturas de educación especial se centra en el conocimiento general sobre discapacidades y trastornos sin profundizar en la realización de adaptaciones curriculares concretas. Este déficit sugiere que la formación inicial del profesorado debe enfatizar más la adaptación de contenidos de acuerdo con las necesidades individuales del alumnado, especialmente en el contexto de las matemáticas, para garantizar una educación inclusiva de calidad como también sugieren Chico, Climent y Gómez-Hurtado (2024) y Chico, Polo-Blanco et al. (2024). Pese a la limitación de la muestra reducida que implica la necesidad de realizar estudios futuros con más EPM que permitan generalizar resultados, los hallazgos destacan la necesidad de formación práctica y específica en adaptaciones curriculares en la enseñanza de la probabilidad. Si bien los y las EPM mostraron competencia en la resolución de problemas matemáticos como ocurría en Alonso-Castaño (2021), sus habilidades para adaptarlos a contextos de diversidad fueron limitadas. Así, sería beneficioso incluir un apartado centrado en la realización de adaptaciones curriculares en disciplinas específicas, como la probabilidad, en la formación docente para garantizar que puedan atender adecuadamente a la diversidad de su futuro alumnado. En este sentido, como línea futura de trabajo, una comparación entre las diferentes menciones del grado podría ofrecer una perspectiva más amplia sobre cómo se abordan las adaptaciones en distintas áreas y disciplinas, permitiendo ajustar la formación de manera más específica. Estos resultados evidencian una carencia formativa en la adaptación de contenidos matemáticos para atender a la diversidad, concretamente en el caso de alumnado con TEA y TEL. Abordar esta limitación desde la formación inicial del profesorado permitiría avanzar hacia una docencia más inclusiva y comprometida con las necesidades reales del aula, fortaleciendo así la calidad educativa y la equidad en el aprendizaje de las matemáticas.

 

Agradecimientos

 

Este trabajo se realizó al amparo del proyecto GRUPIN-IDE/2024/000713 de la Agencia de Ciencia, Competitividad e Innovación Empresarial Asturiana SEKUENS. Pablo Giadas está financiado por los proyectos PID2021-122180OB-100 de la Agencia Estatal de Investigación de España y PAPI-22-PF-12 de la Universidad de Oviedo, en el Plan de Apoyo y Promoción de la Investigación. Los autores Marlén Alonso-Castaño y Pablo Giadas pertenecen a la Red Iberoamericana MTSK (https://redmtsk.net/).

 

REFERENCIAS BIBLIOGRÁFICAS

 

Alonso-Castaño, M. (2021). El conocimiento matemático y pedagógico de los futuros maestros cuando crean y resuelven problemas de probabilidad [Tesis de doctorado, Universidad de Oviedo]. Repositorio de la Universidad de Oviedo.

Alsina, Á. (2016). La estadística y la probabilidad en Educación Primaria. ¿Dónde estamos y hacia dónde debemos ir? Aula de innovación educativa, 251, 12-17.

Alsina, Á. y Vásquez, C. (2016). La probabilidad en Educación Primaria: de lo que debería enseñarse a lo que se enseña. Uno, 71, 46-52.

Alsina, Á., Vásquez, C., Muñiz-Rodríguez, L. y Rodríguez-Muñiz, L.J. (2020). ¿Cómo promover la alfabetización estadística y probabilística en contexto? Estrategias y recursos a partir de la COVID-19 para Educación Primaria. Epsilon, 104, 99-128.

Ball, D.L., Thames, M.H. y Phelps, G. (2008). Content knowledge for teaching: What makes it special? Journal of Teacher Education, 59(5), 389.407. https://doi.org/10.1177/0022487108324554

Batanero, C. (2006). Razonamiento probabilístico en la vida cotidiana: un desafío educativo. En P. Flores y J. Lupiáñez (Eds.), Investigación en el aula de matemáticas. Estadística y Azar (pp.1-17) Sociedad de Educación Matemática Thales.

Batanero, C. y Álvarez-Arroyo, R. (2024). Teaching and learning of probability. ZDM–Mathematics Education, 56(1), 5-17. https://doi.org/10.1007/s11858-023-01511-5

Barrera-Proaño, R.G., Montaño-Salazar, I.K., Hurtado-Toral, C.K., Zapata-Moreira, S.N. y Chuga-Barrera, Y.K. (2024). Adaptaciones curriculares para estudiantes con necesidades educativas especiales no asociadas a una discapacidad: reto para la planificación docente. Ibero-American Journal of Education & Society Research, 4(1), 15-22. https://doi.org/10.56183/iberoeds.v4i1.648

Booth, T., Black-Hawkins, K. y Ainscow, M. (2002). Guía para la evaluación y mejora de la educación inclusiva. Consorcio Universitario para la Educación Inclusiva.

Carrillo, J., Climent, N., Contreras, L.C. y Muñoz-Catalán, M.C. (2013). Determining specialised knowledge for mathematics teaching. En B. Ubuz, Ç. Haser y M.A. Mariotti (Eds.), Proceedings of the CERME 8 (pp. 2985-2994). Middle East Technical University y ERME.

Chico, Á., Climent, N. y Gómez-Hurtado, I. (2024). El uso del Heurísticos y material TEACCH en la Resolución de Problemas con Estudiantes con Autismo-Síndrome de Asperger. Edma 0-6: Educación Matemática en la Infancia, 13(2), 1-17. https://doi.org/10.24197/edmain.2.2024.1-17

Chico, Á., Polo-Blanco, I., Climent, N. y Gómez-Hurtado, I. (2024). Resolución de un problema de generalización por alumnado con trastorno del espectro autista. Enseñanza de las Ciencias, 42(3), 75-96. https://doi.org/10.5565/rev/ensciencias.5990

Confederación Autismo España. (14 de abril de 2021). Hablamos con Ruth Vidriales: El trastorno del espectro del autismo [Archivo de Vídeo]. Youtube. https://www.youtube.com/watch?v=anZSCyIJVEA

Estrada, A., Batanero, C. y Fortuny, J.M. (2003). Actitudes y estadística en profesores en formación y en ejercicio. En Universitat de Lleida (Ed.), Actas del XXVII Congreso Nacional de Estadística e Investigación Operativa. (pp. 909-920). SEIO.

Franco, J. y Alsina, À. (2022). Conocimiento especializado del profesorado de Educación Primaria para enseñar estadística y probabilidad. Educación Matemática, 34(3), 65-96. https://doi.org/10.24844/EM3403.03

Gal, I. (2005). Towards “probability literacy” for all citizens: Building blocks and instructional dilemmas. En G.A. Jones (Ed.), Exploring probability in school: Challenges for teaching and learning (pp. 39-63). Springer US. https://doi.org/10.1007/0-387-24530-8_3

García-Moya, M., González-Ruiz, I. y Polo-Blanco, I. (2023). Argumentos del estudiantado con trastorno del espectro autista al comparar probabilidades simples: un estudio de casos. Bolema: Boletim de Educação Matemática, 37(75), 91-109. https://doi.org/10.1590/1980-4415v37n75a05

Lee, A.M. (2024, 2 abril). Adaptaciones: Qué son y cómo funcionan. Understood. Recuperado el 29 de mayo de 2024, de: https://www.understood.org/es-mx/articles/accommodations-what-they-are-and-how-they-work

Ministerio de Educación y Formación Profesional (2022). Real Decreto 157/2022, de 1 de marzo, por el que se establecen la ordenación y las enseñanzas mínimas de la Educación Primaria. Boletín Oficial del Estado, 52(2 de marzo de 2022), 24386-24504.

Palacios-García, T. (2024). Adaptaciones curriculares y su importancia en estudiantes con necesidades educativas especiales. Cienciamatria. Revista Interdisciplinaria de Humanidades, Educación, Ciencia y Tecnología, 10(18), 313-326. https://doi.org/10.35381/cm.v10i18.1273 

Raigada, J.L.P. (2002). Epistemología, metodología y técnicas de análisis de contenido. Sociolinguistic studies, 3(1), 1-42.

Shulman, L.S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2), 4-14. https://doi.org/10.3102/0013189X015002004

Vidal-Szabó, P. y Estrella, S. (2019). Extensión del modelo MTSK al dominio estadístico. En XV Conferencia Interamericana de Educación Matemática. Recuperado el 25 de mayo de 2024, de: https://conferencia.ciaem-redumate.org/index.php/xvciaem/xv/paper/view/692

 

 

 

Como citar:

Alonso-Castaño, M., Álvarez-Cándano, C. y Giadas, P. (2025). El conocimiento probabilístico de estudiantes para maestro: diseñando y adaptando problemas de probabilidad para alumnado con trastorno de espectro autista. Revista de Educación Estadística, 4, 1-23. https://doi.org/10.29035/redes.4.1.11

 

 

 

 

 

Esta obra está bajo una licencia de Creative Commons
Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional.

 

 

4.  

5.  

   1 *Autor de correspondencia: alonsomarlen@uniovi.es (M. Alonso-Castaño)

   https://orcid.org/0000-0003-0648-7393 (alonsomarlen@uniovi.es)

6. 2 https://orcid.org/0009-0005-6681-3455 (UO282099@uniovi.es)

7. 3 https://orcid.org/0000-0001-5944-523X (giadaspablo@uniovi.es)

9.